
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Т е о р е м а 1. Число сочетаний, размещений и перестановок связаны друг с другом равенством
Т е о р е м а 1. Число сочетаний, размещений и перестановок связаны друг с другом равенством
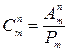 .
.
Т е о р е м а 2. Число сочетаний обладает “симметрией”
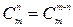 .
.
8.Из 10 кандидатов на одну и ту же должность должны быть выбраны трое. Сколько может быть разных вариантов такого выбора?
Очевидно, что порядок кандидатур не играет роли. Следовательно, речь идет о числе сочетаний. Ответ: 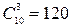 .
.
9.Вычислить 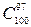 . Воспользуемся теоремой 2.
. Воспользуемся теоремой 2.
Имеем 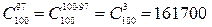 .
.
Теперь, когда определены все виды соединений, можно образовывать из них уравнения и системы уравнений, неравенства и функции. При этом следует лишь помнить, что нижние и верхние индексы должны быть неотрицательными и целыми.
10.Решить уравнение: 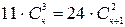 .
.
По определению в выражении 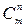 должно быть
должно быть 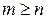 ,
, 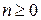 ,
, 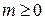 - целые. Тогда ясно, что уравнение имеет смысл лишь при натуральных значениях
- целые. Тогда ясно, что уравнение имеет смысл лишь при натуральных значениях 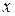 и таких, что
и таких, что 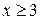 . Теперь расшифруем символы
. Теперь расшифруем символы 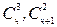 .
.
Имеем
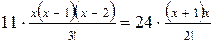
и после очевидных преобразований приходим к квадратному уравнению 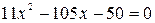 . Его корнями являются числа
. Его корнями являются числа 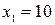 ,
, 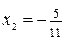 . Учитывая область допустимых значений для исходного уравнения и эквивалентность всех преобразований, получаем ответ
. Учитывая область допустимых значений для исходного уравнения и эквивалентность всех преобразований, получаем ответ 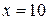 .
.
11. Решить уравнение:
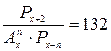 ,
,
где 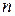 - натуральное число.
- натуральное число.
Очевидно, что 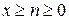 . Расшифровывая символы перестановок и размещений, получаем
. Расшифровывая символы перестановок и размещений, получаем
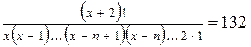 ,
,
или
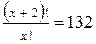 ,
,
или 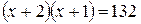 . Отсюда имеем
. Отсюда имеем 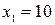 ,
, 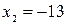 .
.
В качестве ответа может подойти только число 10. Но, кроме того, должно быть по условию 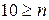 . Таким образом, ответ будет следующим: если
. Таким образом, ответ будет следующим: если 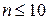 , то
, то 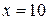 ; если
; если 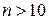 , то уравнение не имеет решений.
, то уравнение не имеет решений.
12. Решить систему уравнений
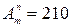 ;
; 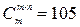 .
.
В этой системе неизвестными являются 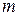 и
и 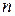 . После расшифровки символов числа размещений и сочетаний легко определяется значение
. После расшифровки символов числа размещений и сочетаний легко определяется значение 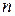 , а потом для
, а потом для 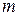 получается квадратное уравнение. В самом деле, имеем
получается квадратное уравнение. В самом деле, имеем
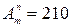 ;
; 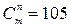 ,
,
или
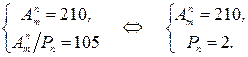
Из второго уравнения получаем подбором, что 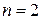 . Тогда первое уравнение принимает вид
. Тогда первое уравнение принимает вид 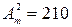 , или
, или 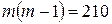 . Решая уравнение, получаем
. Решая уравнение, получаем 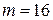 . О т в е т:
. О т в е т: 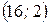 .
.
☼ЗАДАЧИ
ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|