КОМБИНАТОРИКА. ВЕРОЯТНОСТЬ

КОМБИНАТОРИКА. ВЕРОЯТНОСТЬ

§ 1.СОЕДИНЕНИЯ

Приведем определения основных понятий и поясним их на примерах.

О п р е д е л е н и е 1. Различные группы, составленные из каких-либо предметов (элементов) и отличающиеся одна от другой либо числом предметов, либо самими предметами, либо их порядком, называются соединениями.

1. Из 10 различных цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 – можно составить группы по нескольку цифр в каждой: 32 (два элемента), 425 (три элемента), 524 (три элемента), 3801 (четыре элемента) и т. д. Эти группы цифр различаются либо количеством цифр (32 и 3801), либо самими цифрами (135 и 537), либо порядком цифр (425 и 524).

Договоримся обозначать малыми латинскими буквами 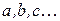элементы, из которых составляются соединения.

Соединения бывают трех типов: размещения, перестановки и сочетания. В этом параграфе мы рассматриваем только те соединения, которые составлены из попарно различных элементов.

О п р е д е л е н и е 2. Размещениями из 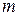элементов по 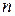называются соединения, каждое из которых содержит 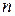элементов, взятых из данных 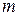элементов, и отличающиеся от других или элементами, или их порядком. Очевидно, что .

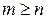Число размещений из 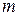элементов по 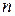обозначается символом 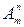и вычисляется по формуле

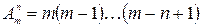Заметим, что произведение в правой части содержит 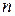множителей, которые являются натуральными числами, последовательно убывающими от 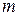до 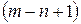. Например,

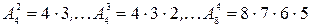и т. д.

2. В классе 10 различных учебных предметов и 5 разных уроков в день. Сколькими способами могут быть распределены уроки в день?

Очевидно, что расписание уроков будет отличаться друг от друга, как самими уроками, так и их порядком. Следовательно, речь идет о размещениях из 10 элементов по 5:

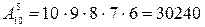3. Сколько можно образовать чисел из цифр 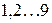, из которых каждое записывалось бы тремя различными цифрами?

Решение его аналогично предыдущему: .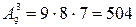

4. Сколько целых чисел можно образовать из всех цифр, каждое из которых записывалось бы тремя различными цифрами?

В задаче речь идет о количестве трехзначных чисел, составляемых из десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. «Хитрое» отличие от предыдущей задачи состоит в том, что среди заданных чисел имеется нуль. Если в группе цифр на первом месте стоит нуль, то число становится двузначным. Поэтому сначала подсчитаем общее число размещений из 10 по 3 и из него вычтем число двузначных чисел с попарно различными цифрами, то есть 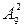. Таким образом, окончательный результат есть

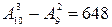О п р е д е л е н и е 3. Перестановками из 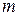элементов называются соединения, каждое из которых содержит только эти 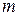элементов в различном порядке. Число перестановок из 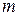элементов обозначается 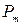и может быть вычислено по формуле

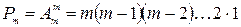Отметим, что произведение 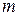последовательных натуральных чисел от 1 до 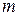включительно обозначается специальным образом

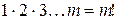Символ 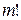читается: эм факториал. По договоренности между математиками используют еще следующую символику:

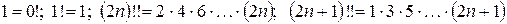В частности, , .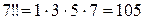

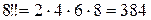5.Количество девятизначных чисел, которые можно записать с помощью цифр 1,2…9, равно .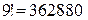

6.Сколькими способами можно разместить12 лиц за столом, на котором поставлено 12 приборов? Ответ очевиден: 12!

7.Выписать все перестановки из трех элементов: 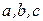. Число таких перестановок равно 3!=6. Имеем

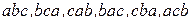О п р е д е л е н и е 4.Сочетаниями из 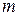элементов по 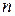называются соединения, каждое из которых содержит 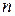элементов, взятых из данных 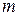элементов, и отличается от других хотя бы одним элементом. Снова понятно, что 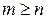. Число сочетаний из 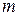элементов по 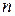обозначается символом 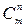и вычисляется по формуле

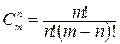Докажите самостоятельно:

12 3 4 5 6 7 Следующая ⇒