
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Случайные события
8.1. ; 8.2. ;
8.3. ; 8.4. ;
8.5. ; 8.6. ;
8.7. ; 8.8. ;
8.9. ; 8.10. ;
8.11. ; 8.12. ;
8.13. ; 8.14. ;
8.15. ; 8.16. ;
8.17. ; 8.18. ;
8.19. ; 8.20. ;
8.21. 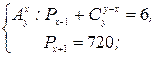 8.22.
8.22. 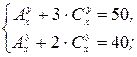
8.23. ;
8.24. ;
8.25. .
Пусть теперь среди заданных элементов имеется некоторое количество одинаковых. Тогда соединения, составленные из этих заданных элементов, называются соединениями с повторениями. Рассмотрим перестановки и сочетания с повторениями.
Пусть дано 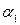 элементов
элементов 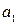 ,
, 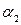 элементов
элементов 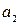 ,…,
,…, 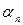 элементов
элементов 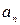 , то есть всего имеется
, то есть всего имеется 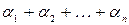 элементов, из которых образовываются перестановки. Число таких перестановок обозначается символом
элементов, из которых образовываются перестановки. Число таких перестановок обозначается символом 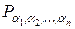 и вычисляется по формуле
и вычисляется по формуле
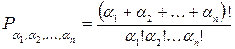 .
.
В частности, перестановки без повторений являются частным случаем:
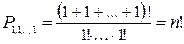
Два сочетания с повторениями из 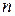 элементов по
элементов по 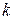 в каждом считаются различными тогда и только тогда, когда они отличаются, по крайней мере, одним элементом или какой-нибудь элемент входит в эти соединения различное число раз. Число сочетаний из
в каждом считаются различными тогда и только тогда, когда они отличаются, по крайней мере, одним элементом или какой-нибудь элемент входит в эти соединения различное число раз. Число сочетаний из 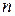 элементов по
элементов по 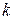 с повторениями обозначается символом
с повторениями обозначается символом 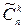 и вычисляется по формуле
и вычисляется по формуле 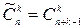 .
.
13. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 2, 2, 3?
Составим какое-нибудь пятизначное число из данных пяти цифр, например 12223, и сделаем всевозможные перестановки цифр. Получим количество чисел, равное 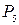 . Но те из чисел, которые получились перестановками одинаковых цифр, дадут и одинаковые числа. В каждом числе можно сделать таких перестановок
. Но те из чисел, которые получились перестановками одинаковых цифр, дадут и одинаковые числа. В каждом числе можно сделать таких перестановок 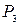 , так как в нем есть три одинаковые цифры 2. Следовательно, искомое количество пятизначных чисел равно
, так как в нем есть три одинаковые цифры 2. Следовательно, искомое количество пятизначных чисел равно 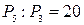 .
.
14.Сколько различных слов можно составить, переставляя буквы слова “математика”? (Заметим, что в задачах на составление слов, мы понимаем под “словом” любую комбинацию букв.)
В заданном слове две буквы “м”, две буквы “т”, три буквы “а”. Поэтому, применяя формулу для числа перестановок с повторениями, получаем
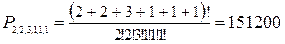 .
.
15. Сколько различных слов можно составить из 12 букв: 4 буквы “а”, 4 буквы “б”, 2 буквы “в”, 2 буквы “г”?
Этот пример является упражнением на применение формулы для числа перестановок с повторениями. Поэтому ограничиваемся только ответом: 29700.
Рассмотрим теперь различные задачи на соединения.
16. Сколькими различными способами можно рассадить за круглым столом компанию, состоящую из 4 мужчин и 4 женщин, чтобы рядом не сидели двое мужчин или две женщины?
Пусть одна женщина заняла определенное место за столом. Три оставшиеся женщины могут разместиться на трех местах через одно (число способов, равное 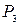 ). На оставшиеся 4 места, при каждом определенном размещении женщин, мужчин можно рассадить числом способов, равным
). На оставшиеся 4 места, при каждом определенном размещении женщин, мужчин можно рассадить числом способов, равным 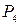 . Следовательно, искомое число способов равно
. Следовательно, искомое число способов равно 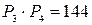 .
.
17.Два участника шахматного турнира выбыли, сыграв только три партии. В результате на турнире сыграно всего 84 партии. Сколько было участников вначале, если они играли друг с другом только по одной партии?
Этот пример – задача на составление уравнения. Пусть искомое число участников турнира равно 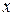 . Со всеми участниками сыграли лишь
. Со всеми участниками сыграли лишь 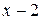 шахматиста (двое выбыли). Число этих партий
шахматиста (двое выбыли). Число этих партий
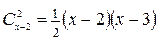
вместе с шестью партиями, сыгранными двумя выбывшими участниками, составляет 84 партии. Получаем уравнение: 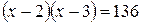 . Решив это квадратное уравнение, найдем два корня, один из которых является отрицательным числом. Но число участников турнира – положительное. Поэтому решением задачи будет лишь второй корень:
. Решив это квадратное уравнение, найдем два корня, один из которых является отрицательным числом. Но число участников турнира – положительное. Поэтому решением задачи будет лишь второй корень: 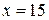 .
.
18. Каким числом способов можно разместить шесть человек за одним круглым столом?
Если не нарушится порядок расположения людей, сидящих у стола, несмотря на их перемещение вокруг него, то можно считать все такие перемещения одинаковыми. Под порядком расположения нужно понимать определенное чередование лиц в одном или другом направлении (по движению часовой стрелки или против), причем само направление значения не имеет. Тогда из 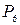 возможных перестановок людей вокруг стола не все будут различными, а именно, каждой перестановке будет соответствовать 12 одинаковых. Поэтому различных способов, которыми можно разместить 6 человек вокруг стола, будет
возможных перестановок людей вокруг стола не все будут различными, а именно, каждой перестановке будет соответствовать 12 одинаковых. Поэтому различных способов, которыми можно разместить 6 человек вокруг стола, будет 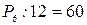 .
.
☼ЗАДАЧИ
ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
8.26. Сколькими способами можно выбрать гласную и согласную буквы из слов: а) подвиг; б) молния; в) сирень?
8.27. Бросают игральную кость с шестью гранями и раскручивают юлу, имеющую 16 граней. Сколькими различными способами они могут упасть?
8.28.Из 5 экземпляров учебника рисования, 9 экземпляров учебника географии, 10 экземпляров учебника физики надо выбрать по одному экземпляру каждого учебника. Сколькими способами это можно сделать?
8.29. В корзине лежат 20 яблок и 14 груш. Петя выбирает из нее яблоко или грушу, после чего его сестра Оля берет и яблоко, и грушу. В каком случае Оля имеет меньшую свободу выбора: если Петя взял яблоко или если он взял грушу?
8.30.У бабушки есть 7 попарно различных конфет, которыми она угощает 10 внуков так, что каждый получает либо одну конфету, либо ничего. Сколькими способами можно распределить конфеты между внуками?
8.31. В велосипедном клубе состоит 80 членов. Требуется выставить команду из 3 человек для участия в велопробеге. Сколькими способами можно это сделать?
8.32. В классе 9 мальчиков и 6 девочек. Надо выбрать 8 человек так, чтобы среди них было не менее 4 девочек. Сколькими способами это можно сделать?
8.33. Сколькими способами можно расставить 25 книг в книжном шкафу с 6 полками, если каждая полка может вместить все 25 книг?
8.34. Сколькими способами можно выбрать на шахматной доске белый и черный квадраты, не лежащие на одной и той же горизонтали и вертикали?
8.35. Из города А в город В ведут 6 дорог, а из города В в город С – четыре дороги. Сколько путей, проходящих через В, ведут из А в С?
8.36.На вершину горы ведут 6 дорог. Сколькими способами турист может подняться в гору и спуститься с нее? Тот же вопрос при условии, что подъем и спуск происходят разными путями.
8.37. Построить графики следующих функций и уравнений:
1)  ; 2)
; 2) 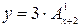 ; 3)
; 3) 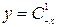 ;
;
4) 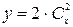 ; 5)
; 5) 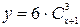 ; 6)
; 6) 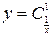 ;
;
7) 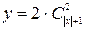 ; 8)
; 8) 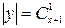 ; 9)
; 9) 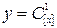 ;
;
10) 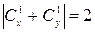 ; 11)
; 11) 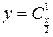 ; 12)
; 12) 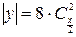 .
.
8.38.Решить неравенства:
1) 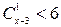 ; 2)
; 2) 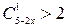 ; 3)
; 3) 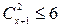 ;
;
4) 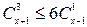 ; 5)
; 5) 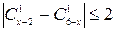 ; 6)
; 6) 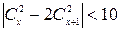 ;
;
7) 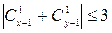 ; 8)
; 8) 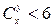 ; 9)
; 9) 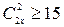 .
.
§ 2. БИНОМ НЬЮТОНА 
Для любого натурального 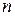 и любых чисел
и любых чисел 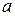 и
и 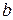 справедлива формула разложения бинома Ньютона
справедлива формула разложения бинома Ньютона
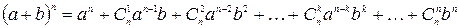 .
.
Коэффициенты 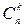 называются биномиальными коэффициентами, и они равны числу сочетаний из
называются биномиальными коэффициентами, и они равны числу сочетаний из 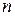 элементов по
элементов по 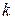 . Общий член разложения обозначается символом
. Общий член разложения обозначается символом 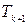 и по определению
и по определению
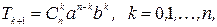
где 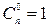 .
.
При решении задач часто используются следующие свойства бинома:
1.Число всех членов разложения равно 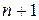 .
.
2.Сумма показателей при 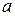 и
и 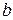 в каждом члене одна и та же: она равна показателю степени бинома. При этом степени
в каждом члене одна и та же: она равна показателю степени бинома. При этом степени 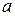 убывают последовательно от
убывают последовательно от 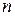 до 0, а степени
до 0, а степени 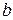 возрастают также последовательно от 0 до
возрастают также последовательно от 0 до 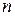 .
.
3.Коэффициенты членов, одинаково удаленных от концов разложения, равны между собой.
4.Если показатель бинома 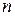 есть четное число, то разложение бинома содержит нечетное число членов, среди которых имеется одно слагаемое, одинаково удаленное от концов разложения. Это слагаемое имеет наибольший биномиальный коэффициент. Если же показатель бинома
есть четное число, то разложение бинома содержит нечетное число членов, среди которых имеется одно слагаемое, одинаково удаленное от концов разложения. Это слагаемое имеет наибольший биномиальный коэффициент. Если же показатель бинома 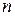 есть нечетное число, то разложение бинома содержит два члена с максимальными биномиальными коэффициентами, равными по величине. Эти члены стоят в середине разложения. Например, если
есть нечетное число, то разложение бинома содержит два члена с максимальными биномиальными коэффициентами, равными по величине. Эти члены стоят в середине разложения. Например, если 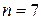 , то номера членов с максимальными коэффициентами равны 4 и 5. Например,
, то номера членов с максимальными коэффициентами равны 4 и 5. Например,
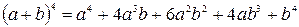 ,
,
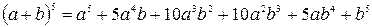 .
.
5.Из сравнения двух рядом стоящих членов разложения бинома
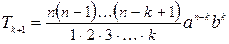 ,
,
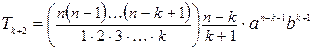
делаем вывод, что для получения коэффициента следующего члена достаточно умножить коэффициент предыдущего члена на показатель буквы 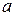 в этом члене и разделить на число членов, предшествующих определяемому.
в этом члене и разделить на число членов, предшествующих определяемому.
Пользуясь этим свойством, можно сразу писать, например,
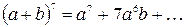
Коэффициент 7 умножаем на показатель степени 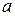 , то есть на 6, и делим на число выписанных членов, таким образом, на 2, получаем 21:
, то есть на 6, и делим на число выписанных членов, таким образом, на 2, получаем 21:
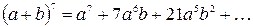
Теперь повторим описанные действия. Коэффициент 21 умножаем на 5 и делим на 3, получаем 35:
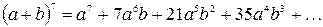
Таким образом, выписаны члены до середины разложения бинома. Остальные члены получим, основываясь на симметрии коэффициентов (свойство 3):
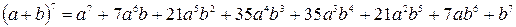 .
.
6.Сумма всех биномиальных коэффициентов равна 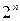 .
.
7.Сумма биномиальных коэффициентов, стоящих на нечетных местах, равна сумме биномиальных коэффициентов, стоящих на четных местах.
8.Для любых натуральных 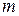 и
и 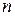 таких, что
таких, что 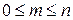 верно равенство
верно равенство 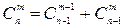 . (8. 1)
. (8. 1)
9.Тождество (8.1) позволяет вычислить значения 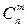 , зная значения
, зная значения 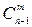 и
и 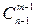 . Если это делать последовательно для
. Если это делать последовательно для 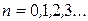 и всех
и всех 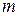 таких, что
таких, что 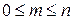 , то результаты вычислений дадут треугольник Паскаля:
, то результаты вычислений дадут треугольник Паскаля:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
…………………………………………..
Р е к о м е н д а ц и я: проанализируйте эту таблицу, найдите закон ее составления и продолжите ее на несколько строк.
Приведем теперь несколько примеров на свойства бинома Ньютона.
19. Найти показатель бинома 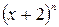 , зная, что десятый член разложения этого бинома имеет наибольший коэффициент.
, зная, что десятый член разложения этого бинома имеет наибольший коэффициент.
Используя формулу общего члена разложения, имеем систему неравенств
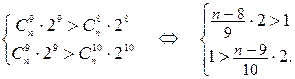
Решая эти неравенства, получаем, что 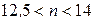 . Следовательно, показатель бинома
. Следовательно, показатель бинома 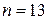 .
.
20.Доказать, что наибольший коэффициент разложения 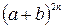 есть число четное.
есть число четное.
Наибольший коэффициент разложения 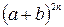 есть коэффициент
есть коэффициент 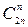 у
у 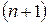 -го члена. Покажем, что он – четное число. Имеем
-го члена. Покажем, что он – четное число. Имеем
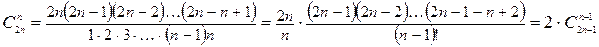 .
.
21. Найти 5-й член разложения бинома 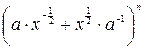 , если отношение коэффициента 3-го члена ко второму равно
, если отношение коэффициента 3-го члена ко второму равно 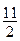 .
.
По условию 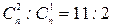 , откуда вычисляем показатель степени бинома:
, откуда вычисляем показатель степени бинома: 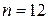 . По формуле общего члена разложения бинома
. По формуле общего члена разложения бинома
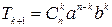
пишем пятый член заданного бинома:
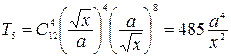 .
.
22. Чему равна степень 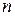 , в которую необходимо возвести бином
, в которую необходимо возвести бином 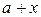 , чтобы коэффициент при
, чтобы коэффициент при 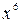 равнялся
равнялся 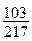 ?
?
Задача не имеет решения, так как биномиальные коэффициенты могут быть только целыми числами.
23. В разложении 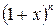 найти значение показателя
найти значение показателя 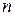 , если известно, что коэффициент пятого члена равен коэффициенту девятого члена.
, если известно, что коэффициент пятого члена равен коэффициенту девятого члена.
По условию имеем: 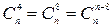 . Отсюда следует, что
. Отсюда следует, что 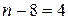 ,
, 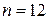 .
.
24. Найти коэффициент при 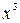 в многочлене
в многочлене
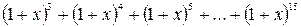 .
.
Данный многочлен записан в виде суммы геометрической прогрессии. Первый член прогрессии есть 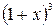 , знаменатель прогрессии равен
, знаменатель прогрессии равен 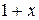 . Поэтому имеем
. Поэтому имеем
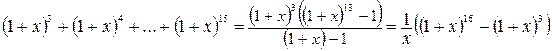 .
.
При условии, что в знаменателе находится 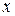 , для получения члена с
, для получения члена с 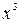 в числителе найдем член с
в числителе найдем член с 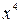 . Такой член есть только в разложении
. Такой член есть только в разложении 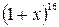 и коэффициент при нем является искомым.
и коэффициент при нем является искомым.
О т в е т: 1820.
☼ЗАДАЧИ
ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
8.39. Найти наименьшее значение показателя 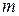 в разложении
в разложении 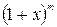 , при котором отношение двух соседних коэффициентов разложения равнялось бы отношению 7:15.
, при котором отношение двух соседних коэффициентов разложения равнялось бы отношению 7:15.
8.40. В разложении бинома 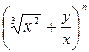 определить член разложения бинома, не содержащий переменную
определить член разложения бинома, не содержащий переменную 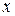 , если биномиальный коэффициент 3-го члена разложения на 5 больше биномиального коэффициента 2-го члена разложения.
, если биномиальный коэффициент 3-го члена разложения на 5 больше биномиального коэффициента 2-го члена разложения.
8.41. Найти члены, не содержащие иррациональности, в разложении бинома 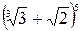 .
.
8.42. При каких значениях 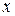 третий член разложения
третий член разложения 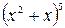 равен 1000000000?
равен 1000000000?
8.43. Некоторый член разложения 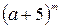 имеет коэффициент, равный 853125, его биномиальный коэффициент равен 1365. Найти показатель бинома
имеет коэффициент, равный 853125, его биномиальный коэффициент равен 1365. Найти показатель бинома 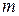 и номер
и номер 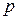 этого члена.
этого члена.
8.44. Найти член разложения 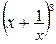 , не содержащий
, не содержащий 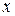 .
.
8.45. В разложении бинома
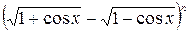
биномиальный коэффициент 3-го члена разложения равен 28. Найти средний член разложения.
8.46. Найти третий член разложения
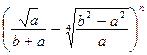 ,
,
если биномиальный коэффициент четвертого члена равен 20.
8.47. Чему равна степень 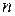 , в которую надо возвести бином
, в которую надо возвести бином 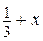 , чтобы биномиальный коэффициент при
, чтобы биномиальный коэффициент при 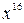 равнялся
равнялся 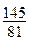 ?
?
8.48. В разложении 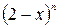 найти значение
найти значение 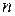 , если: а) биномиальный коэффициент пятого члена равен биномиальному коэффициенту девятого члена, б) биномиальный коэффициент пятого члена относится к биномиальному коэффициенту 2-го члена как 22:15, в) отношение двух соседних биномиальных коэффициентов разложения есть
, если: а) биномиальный коэффициент пятого члена равен биномиальному коэффициенту девятого члена, б) биномиальный коэффициент пятого члена относится к биномиальному коэффициенту 2-го члена как 22:15, в) отношение двух соседних биномиальных коэффициентов разложения есть 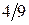 (указать наименьшее двузначное и трехзначное значение
(указать наименьшее двузначное и трехзначное значение 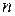 ).
).
8.49. В разложении бинома 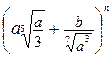
найти член, содержащий переменную 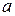 в третьей степени, если сумма биномиальных коэффициентов равна: а) 2048, б) 4096, в) 10192.
в третьей степени, если сумма биномиальных коэффициентов равна: а) 2048, б) 4096, в) 10192.
8.50. В разложении бинома 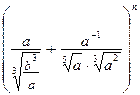
определить член разложения, не содержащий букву 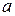 , если сумма биномиальных коэффициентов трех первых членов разложения равна: 1) 56, 2) 79.
, если сумма биномиальных коэффициентов трех первых членов разложения равна: 1) 56, 2) 79.
8.51. Найти все члены, не содержащие иррациональности в разложении следующих биномов:
а) 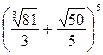 ; б)
; б) 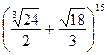 ; в)
; в) 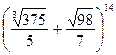 .
.
8.52. Найти все значения параметра 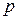 , при которых разложение бинома
, при которых разложение бинома 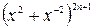 имеет член, содержащий степень
имеет член, содержащий степень 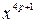 .
.
8.53. Двум бригадам рабочих была уплачена сумма денег в рублях, равная умноженному на 1000 коэффициенту того члена разложения бинома
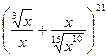 ,
,
который содержит 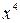 . Число тысяч рублей, полученных каждым рабочим первой бригады, равно числу членов арифметической прогрессии, у которой
. Число тысяч рублей, полученных каждым рабочим первой бригады, равно числу членов арифметической прогрессии, у которой 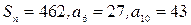 . Число тысяч рублей, полученных каждым рабочим второй бригады, равно корню уравнения
. Число тысяч рублей, полученных каждым рабочим второй бригады, равно корню уравнения 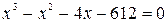 . Сколько рабочих было в каждой бригаде, если в первой бригаде было на 3 человека больше, чем во второй?
. Сколько рабочих было в каждой бригаде, если в первой бригаде было на 3 человека больше, чем во второй?
§3. СЛУЧАЙНЫЕ СОБЫТИЯ. ВЕРОЯТНОСТЬ.
Случайные события
Событие 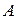 называется достоверным относительно условий
называется достоверным относительно условий 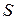 , если оно обязательно наступает при соблюдении условий
, если оно обязательно наступает при соблюдении условий 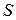 .
.
Событие 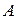 называется невозможным относительно условий
называется невозможным относительно условий 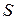 , если оно никогда не наступит при соблюдении условий
, если оно никогда не наступит при соблюдении условий 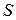 .
.
Событие 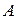 называется случайным относительно условий
называется случайным относительно условий 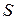 , если оно может наступить при соблюдении условий
, если оно может наступить при соблюдении условий 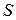 .
.
Создание условий 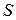 называется испытанием по отношению к событию
называется испытанием по отношению к событию 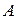 . События
. События 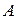 и
и 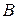 называются несовместными, если появление одного из них исключает появление другого при одном и том же испытании. В противном случае события
называются несовместными, если появление одного из них исключает появление другого при одном и том же испытании. В противном случае события 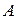 и
и 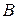 называются совместными.
называются совместными.
События 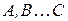 называются единственно возможными при данном испытании, если появление одного и только одного из них является достоверным событием.
называются единственно возможными при данном испытании, если появление одного и только одного из них является достоверным событием.
События 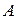 и
и 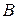 называются равновозможными, если нет оснований считать, что ни одно из них не является более возможным, чем другое.
называются равновозможными, если нет оснований считать, что ни одно из них не является более возможным, чем другое.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|