
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Формула Бернулли
Формула Бернулли
Пусть проведено 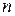 независимых испытаний, в каждом из которых может произойти событие
независимых испытаний, в каждом из которых может произойти событие 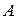 с одной и той же вероятностью
с одной и той же вероятностью 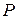 . Тогда вероятность
. Тогда вероятность 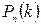 того, что это событие наступит ровно
того, что это событие наступит ровно 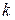 раз (неважно в каком порядке) определяется по формуле Бернулли
раз (неважно в каком порядке) определяется по формуле Бернулли
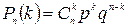 , где
, где 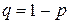 .
.
5.Вероятность того, что ученик знает тригонометрические формулы, равна 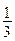 . Учитель считает, что класс удовлетворительно выучил формулы, если при фронтальном опросе всего класса из 27 человек правильные ответы дали
. Учитель считает, что класс удовлетворительно выучил формулы, если при фронтальном опросе всего класса из 27 человек правильные ответы дали 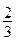 ученического коллектива. Какова вероятность того, что класс знает эти формулы удовлетворительно при условии, что каждый ученик дает свой ответ, не зная ответов своих товарищей?
ученического коллектива. Какова вероятность того, что класс знает эти формулы удовлетворительно при условии, что каждый ученик дает свой ответ, не зная ответов своих товарищей?
Решение задачи дает формула Бернулли:
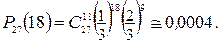
☼ЗАДАЧИ
ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
8.79. Две равные по силе команды волейболистов проводят между собой турнир. Что более вероятно выиграть: три партии из пяти или две партии из трех?
8.80. Монету бросают 10 раз. Найти вероятность того, что герб выпадает: а) не менее 3-х раз; б) не более 3-х раз; в) не менее 3-х, но не более 5 раз.
8.81. В ночное поехали 12 мальчишек. Они на лугу разожгли 3 костра. Какова вероятность того, что у второго костра сели 6 мальчишек?
8.82. Рабочий обслуживает 10 одинаковых станков. Вероятность того, что в течение рабочей смены станок потребует ремонта, равна 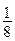 . Какова вероятность того, что в течение смены рабочему придется ремонтировать 5станков?
. Какова вероятность того, что в течение смены рабочему придется ремонтировать 5станков?
§4. СЛУЧАЙНАЯ ВЕЛИЧИНА И ЕЕ ХАРАКТЕРИСТИКИ.
Определение 1. Случайной называют величину 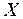 , 1) которая в результате испытания может принять одно и только одно из возможных значений
, 1) которая в результате испытания может принять одно и только одно из возможных значений 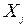 ; 2) событие
; 2) событие 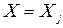 является случайным.
является случайным.
Определение 2. Случайную величину называют дискретной, если она может принимать только отдельные изолированные значения с определенными вероятностями.
Определение 3. Случайную величину называют непрерывной, если она может принимать все значения из некоторого промежутка (конечного или бесконечного).
Дискретная случайная величина задается законом распределения.
Определение 4. Законом распределения дискретной случайной величины называется набор всех возможных ее значений и их вероятностей.
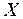
| 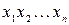
|
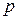
| 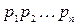
|
где 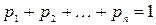 .
.
Примеры:
1. Биномиальный закон распределения (число появлений события в 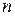 испытаниях):
испытаниях):
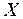
| 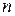
| 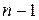
| 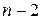
| … | 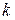
| … | 0 |
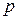
| 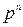
| 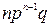
| 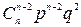
| … | 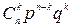
| 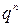
|
2. Закон распределения Пуассона вероятностей массовых редких событий:
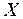
| 0 | 1 | 2 | … | 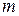
| … |
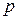
| 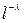
| 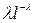
| 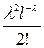
| … | 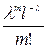
| … |
где 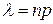 ,
, 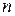 – очень большое число испытаний,
– очень большое число испытаний, 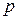 – очень малая вероятность появления события.
– очень малая вероятность появления события.
Поведение дискретных случайных величин описывается следующими числовыми характеристиками.
Определение 5. Математическим ожиданием 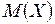 дискретной случайной величины
дискретной случайной величины 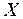 называют сумму произведений всех ее возможных значений на их вероятности:
называют сумму произведений всех ее возможных значений на их вероятности:
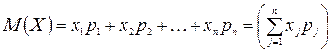 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|