
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Жарық шашыраудың толқын ұзындығына, бөлшектердің өлшемдеріне тәуелділігі.
Жарық тың шашырауы, немесе опалесценция, дифракциялық қ ұ былыс болып табылады, ол тү сетін жарық толқ ын ұ зындығ ынан кіші ә ртектіліктерден туады (обусловлен неоднородностями). Мұ ндай ә ртектіліктер жарық та барлық бағ ытта шашыратады. Жарық тың шашырау теориясын алғ аш Рэлей жасағ ан. Оның негізінде сфералық диэлектрлі бө лшектері бар жү йенің кө лем бірлігі шашыратқ ан жарық тың ү демелілігін есептейтін тең деу жатыр. Бө лшектердің ө лшемі тү скен жарық тың тоқ ынынан кө п кіші болоды:
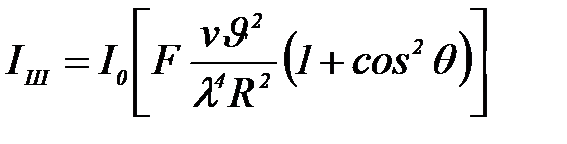
мұ ндағ ы: 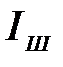 – сыну кө рсеткіштері функциясы;
– сыну кө рсеткіштері функциясы;
v – жү йенің уө лем бірлігіндегі бө лшектер концентрациясы;
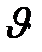 – бө лшек кө лемі;
– бө лшек кө лемі;
l – тү скен жарық толқ ын ұ зындығ ы;
R – бө лшектің жарық кө зінен ара қ ашық тығ ы;
q – тү скен жарық пен шашырағ ан жарық бағ ыттары арасындағ ы бұ рыш;
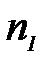 жә не
жә не 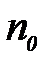 – дисперстік фаза мен дисперстік орта заттарының сыну кө рсеткіштері. Рэлей тең деуі ультрамикроскопиялық, нефелометрия, турбидиметрия негізі болып табылады.
– дисперстік фаза мен дисперстік орта заттарының сыну кө рсеткіштері. Рэлей тең деуі ультрамикроскопиялық, нефелометрия, турбидиметрия негізі болып табылады.
Ультрамикроскопияның микроскопиядан айырмашылығ ы дисперстік жү йе бір қ апталынан жарық танады да, шашырағ ан жарық бақ ыланады. Нә тижесінде бө лшектер жарық нү ктелері тә різді болады.  бө лшектерді бақ ылауғ а болады.
бө лшектерді бақ ылауғ а болады.
Нефелометрия – дисперстік жү йе қ ұ йылғ ан кюветағ а тү сірілген жарық тың шашырағ аннан кейінгі ү демелігін ө лшеуге негізделген. Ә детте, кө лемдік концентрация с белгілі не табуғ а болады, сондық тан Рэлей тең деуін

мұ ндағ ы: k – константа; 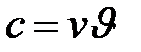 – дисперстік жү йе кө лемінің концентрациясы.
– дисперстік жү йе кө лемінің концентрациясы.
Стандарт жү йедегі с немесе 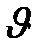 біле отырып, дисперстік жү йе ү шін есептеуге болады.
біле отырып, дисперстік жү йе ү шін есептеуге болады.
Турбидиметрия дисперстік жү йе арқ ылы ө ткен жарық тың ү демелілігін ө лшеуге негізделген. Шашырағ ан жарық ты жұ тылғ ан деп болжап жарық тың шашырау заң дылық тары Бугер – Ламберт – Бер заң ына бағ ынады деуге болады:
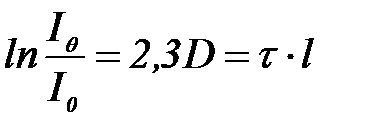
мұ ндағ ы: 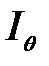 – жү йе арқ ылы ө ткен жарық ү демелілігі;
– жү йе арқ ылы ө ткен жарық ү демелілігі; 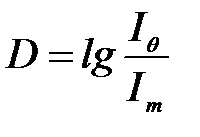 – оптикалық тығ ыздық; τ – жү йенің лайлануы; l – жү йе қ абатының қ алың дығ ы.
– оптикалық тығ ыздық; τ – жү йенің лайлануы; l – жү йе қ абатының қ алың дығ ы.
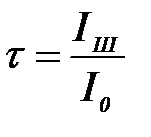 , яғ ни
, яғ ни 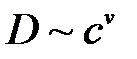 жә не
жә не 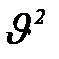 . Олай болса, D бойынша (стандарт жү йелермен салыстыру арқ ылы) бө лшектің ө лшемін жә не концентрациясын анық тауғ а болады.
. Олай болса, D бойынша (стандарт жү йелермен салыстыру арқ ылы) бө лшектің ө лшемін жә не концентрациясын анық тауғ а болады.
Мысал №1. Толқ ын ұ зындығ ы 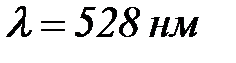 жарық ағ ыны
жарық ағ ыны 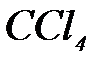 – ң судағ ы эмульсиясы арқ ылы ө ткенде жарық тың шашырауы нә тижесінде 2 есе ә лсірейді.
– ң судағ ы эмульсиясы арқ ылы ө ткенде жарық тың шашырауы нә тижесінде 2 есе ә лсірейді.
Эмульсия қ абатының қ алың дығ ы 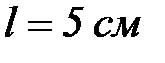 . Дисперстік фаза бө лшектерінің кө лемдік ү лесі
. Дисперстік фаза бө лшектерінің кө лемдік ү лесі 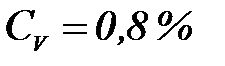 ,
, 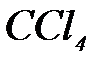 – ң сыну кө рсеткіші
– ң сыну кө рсеткіші 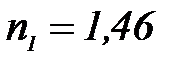 , судың
, судың 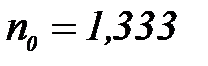 . Жарық Рэлей тең деуіне сә йкес шашырайды жә не Бугер – Ламберт – Бер тең деуі бойынша ә лсірейді. Дисперстік фаза бө лшектерінің радиустарын есептең із.
. Жарық Рэлей тең деуіне сә йкес шашырайды жә не Бугер – Ламберт – Бер тең деуі бойынша ә лсірейді. Дисперстік фаза бө лшектерінің радиустарын есептең із.
Шығ арылуы. Дисперстік жү йенің бірлік кө лемі барлық бағ ытта шашырататын жарық ү демелілігіне арналғ ан Рэлей тең деуі:
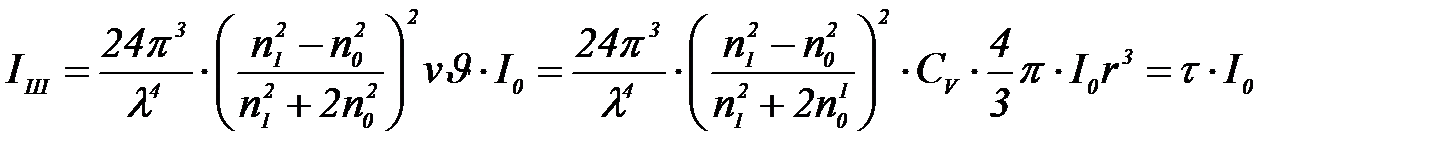
Ақ золь арқ ылы ө ткенде жарық ү демелілігі Бугер – Ламберт – Бер тең деуі бойынша азаяды:
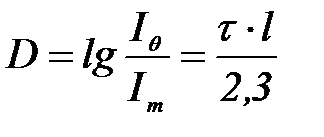
Есеп шарты бойынша: 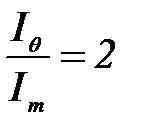
Олай болса, 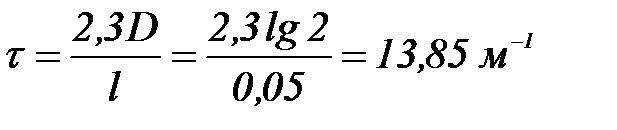
τ шамасын Рэлей тең деуіне қ ойып, эмульсия тамшыларының радиусын табамыз:
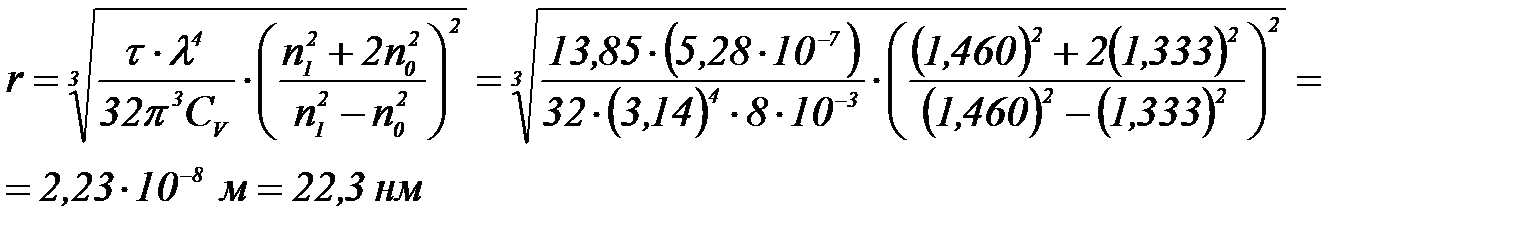
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|