
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Коллоидтық жүйелердің молекулалық - кинетикалық қасиеттері
СОӨ Ж №2
Коллоидтық жү йелердің молекулалық - кинетикалық қ асиеттері
Диффузия коэффициентін, орташа квадраттық ығ ысуды анық тау
Микрогетерогенді жү йелерде (суспензия, эмульсия, газдық эмульсиялар, аэрозольдер) массаларының ү лкен болуына байланысты бө лшектер жылулық (броундық ) қ озғ алысқ а қ атыса алмайды, тұ ну – седиментация немесе кері процесс – бө лшектердің қ алқ ып шығ уы байқ алады. Егер бө лшектер ағ ынының қ озғ алыстағ ы ламинарлы жә не Стокс заң ына бағ ынса, гравитациялық ө рісте бө лшектердің тұ ну (қ алқ ып шығ у) жылдамдығ ы келесі қ атынаспен беріледі.
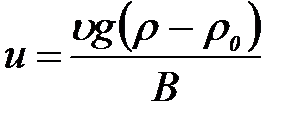
мұ ндағ ы: В – ү йкеліс коэффициенті; u – бө лшек кө лемі; g – еркін тү су ү деуі; r жә не 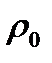 – бө лшек пен дисперстік орта тығ ыздығ ы.
– бө лшек пен дисперстік орта тығ ыздығ ы.
Сфералық бө лшектер ү шін 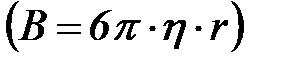 тең деу келесі тү рге келеді:
тең деу келесі тү рге келеді:
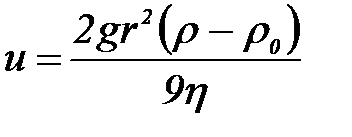
мұ ндағ ы: r – бө лшек радиусы; h – дисперстік орта тұ тқ ырлығ ы.
Жү йенің седиментациялануғ а қ абілеттігі седиментация константасымен анық талады:
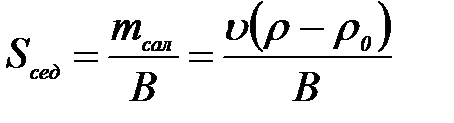
Мұ ндағ ы: 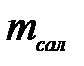 – бө лшектің салыстырмалы массасы (орта тығ ыздық ты ескергенде;
– бө лшектің салыстырмалы массасы (орта тығ ыздық ты ескергенде; 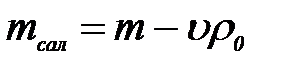 )
)
Сфералық бө лшектер ү шін:
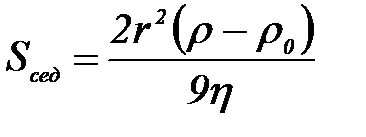
Центрден тепкіш ө рісте седиментацияланғ ан бө лшектердің жолы х уақ ыт t – мен бірге экспонента бойымен ө седі (центрифуганың айналу саны тұ рақ ты болғ анда).
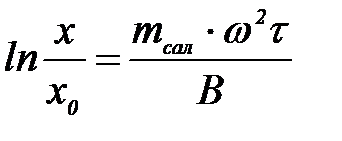
Бө лшектер сфералық болса, онда
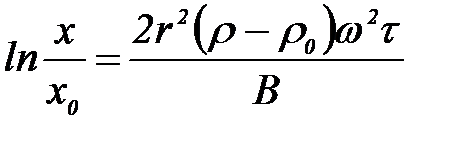 ;
;
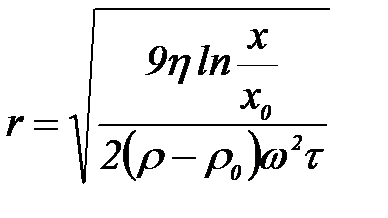
мұ ндағ ы:  – айналу орталығ ынан бө лшектің бастапқ ы ара қ ашық тағ ы; w – центрифуга роторының бұ рыштық айналу жылдамдығ ы.
– айналу орталығ ынан бө лшектің бастапқ ы ара қ ашық тағ ы; w – центрифуга роторының бұ рыштық айналу жылдамдығ ы.
Жоғ арыдағ ы қ атынастар ә р тү рлі материалдардың дисперстігінің седиментациялық анализінде қ олданылады.
Ультромикрогетерогенді жү йелер (зольдер) бө лшектері жылулық қ озғ алысқ а қ атысады, олар молекула – кинетикалық заң дарғ а бағ ынады.
Бө лшектердің орташа ығ ысуы 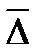 мен диффузия коэффициентінің арасындағ ы байланысты Эйнштейн – Смолуховский заң ы кө рсетеді:
мен диффузия коэффициентінің арасындағ ы байланысты Эйнштейн – Смолуховский заң ы кө рсетеді:
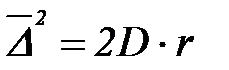
мұ ндағ ы: t – қ озғ алыстағ ы бө лшектердің ара қ ашық тығ ын ө лшеу моменттері арасындағ ы уақ ыт.
Зольдерге диффузия коэффициентіне арналғ ан Эйнштейн тең деуі қ олданылады. Егер сфералық бө лшектер болса,
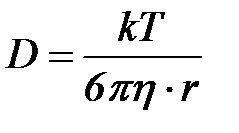
Лиозольдер ү шін Вант – Гоффтың осмостық заң ы орындалады (ә детте, ерітіндіге қ атысты):
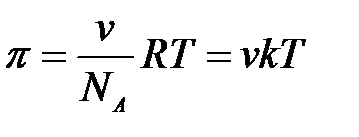
мұ ндағ ы: p – осмостық қ ысым; n – зольдің кө лем бірлігіндегі бө шектер саны, бө лшектік концентрация.
Аэрозольдер Клайперон – Менделеевтің газдық заң ын пайдалануғ а болады:
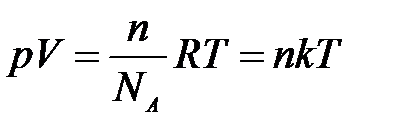
мұ ндағ ы: п – аэрозольдегі бө лшектер саны.
Ультромикрогетерогенді жү йелер тұ нғ анда седиментацияғ а кері бағ ытта бө лшектердің диффузиясының қ озғ аушы кү ші болып табылатын концентрациялар градиенті туады.
Диффузиялық жә не седиментациялық ағ ындар тең ескенде, диффузия – седиментациялық тепе – тең дік орнайды.
h биіктігінде бө лшектің концентрациясы
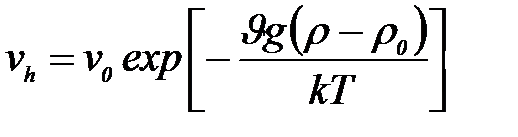
мұ ндағ ы: 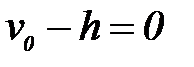 биіктігінде бө лшектер концентрациясы.
биіктігінде бө лшектер концентрациясы.
Седиментациялық термодинамикалық тұ рақ тылық ө лшемі – 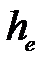 биіктігі бойында дисперстік фаза концентрациясы е есе ө згереді:
биіктігі бойында дисперстік фаза концентрациясы е есе ө згереді:
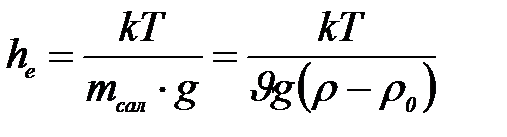
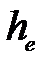 неғ ұ рлым ү лкен болса, соғ ұ рлым жү йе седиментацияғ а термодинамикалық тұ рақ ты болады. Температура ө скен сайын, бө лшектер размері, орта мен дисперстік фаза тығ ыздық тары азайғ ан сайын тұ рақ тылық ө згереді.
неғ ұ рлым ү лкен болса, соғ ұ рлым жү йе седиментацияғ а термодинамикалық тұ рақ ты болады. Температура ө скен сайын, бө лшектер размері, орта мен дисперстік фаза тығ ыздық тары азайғ ан сайын тұ рақ тылық ө згереді.
Седиментацияғ а кинетикалық тұ рақ тылық ө лшемі седиментация константасына кері шама:
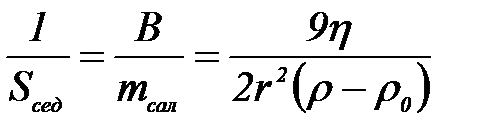
Кинетикалық тұ рақ тылық ты тұ тқ ырлық, орта тығ ыздығ ы, бө лшектердің тығ ыздығ ы мен размерін ө згерту арқ ылы реттеп отыруғ а болады.
Мысал №1. 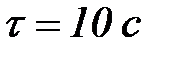 ішінде гидрозоль бө лшектерінің орташа квадраттық ығ ысуы мен диффузиялық коэффициентін анық таң ыз. Бө лшектердің радиусы
ішінде гидрозоль бө лшектерінің орташа квадраттық ығ ысуы мен диффузиялық коэффициентін анық таң ыз. Бө лшектердің радиусы 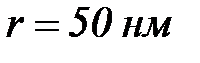 , тә жірибелік температура 293К, орта тұ тқ ырлығ ы
, тә жірибелік температура 293К, орта тұ тқ ырлығ ы 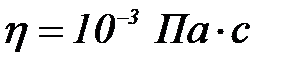
Шығ арылуы: Эйнштейн – Смолуховский заң ын пайдаланамыз:
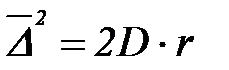
Диффузиялық коэффициентін Эйнштейн тең деуі бойынша табамыз:
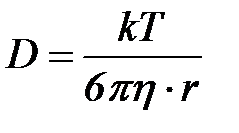
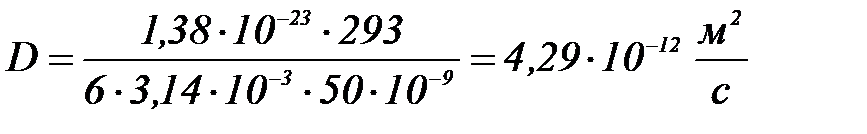
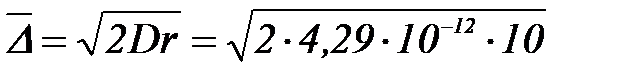
Мысал №2. 293К – де диффузиялық – седиментация тепе – тең дік орнағ анда 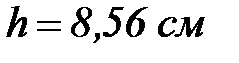 биіктікте алтын гидрозолі бө лшектерінің концентрациясы е есе ө згереді, бө лшектердің радиусын табың ыз. Алтын тығ ыздығ ы
биіктікте алтын гидрозолі бө лшектерінің концентрациясы е есе ө згереді, бө лшектердің радиусын табың ыз. Алтын тығ ыздығ ы 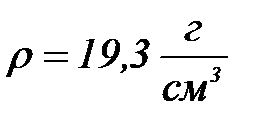 , су тығ ыздығ ы
, су тығ ыздығ ы 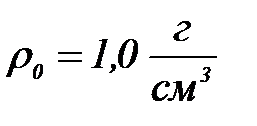 .
.
Шығ арылуы: Диффузиялық – седиментация тепе – тең дік орнағ анда бө лшектің биіктік бойынша тартылуы гипсометрлік тең деумен ө рнектеледі:
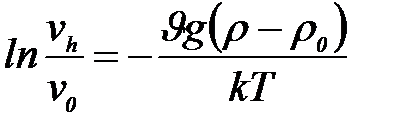
мұ ндағ ы: 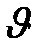 – бө лшек кө лемі, сфералық бө лшектер ү шін
– бө лшек кө лемі, сфералық бө лшектер ү шін 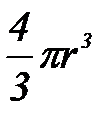 . Есеп шарты бойынша
. Есеп шарты бойынша 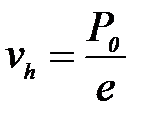 жә не
жә не 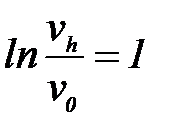 . Олай болса,
. Олай болса,
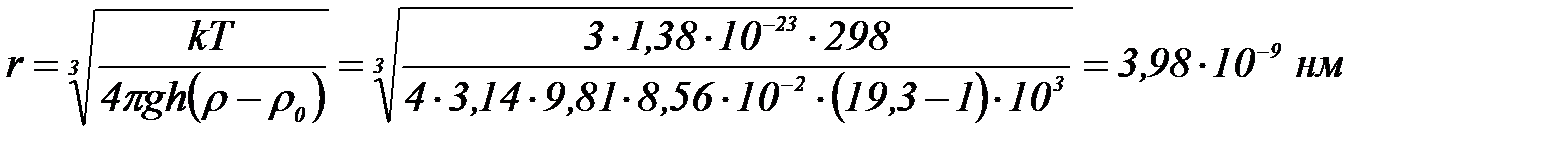
Мысал №3. 30% – тік 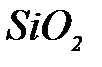 гидрозолінің 293К температурадағ ы осмостық қ ысымын есептең із. Бө лшектің меншікті беті
гидрозолінің 293К температурадағ ы осмостық қ ысымын есептең із. Бө лшектің меншікті беті 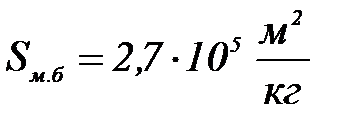 . Гидрозоль бө лшектерінің тығ ыздығ ы
. Гидрозоль бө лшектерінің тығ ыздығ ы 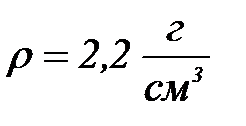 , орта тығ ыздығ ы
, орта тығ ыздығ ы 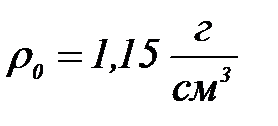 .
.
Шығ арылуы: Дисперстік жү йелердің осмостық қ ысымы Вант – Гофф тең деуімен есептеледі:
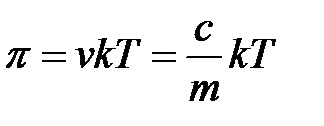
мұ ндағ ы: с – массалық концентрация, т – бір бө лшек массасы.
Дисперстік фазаның массалық концентрациясы:
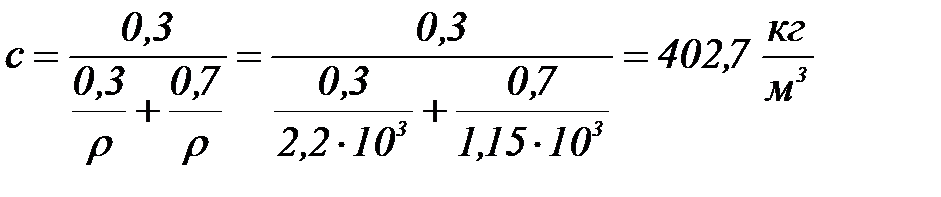
Сфералық бө лшектер ү шін 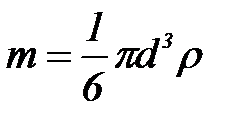 .
. 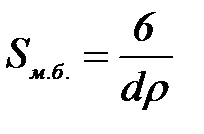 болғ андық тан,
болғ андық тан, 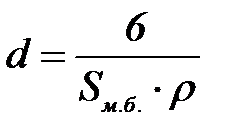
Сонда 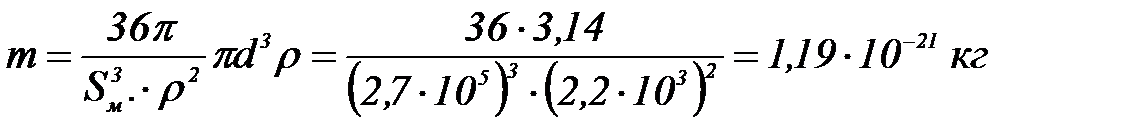 .
.
Осмостық қ ысым: 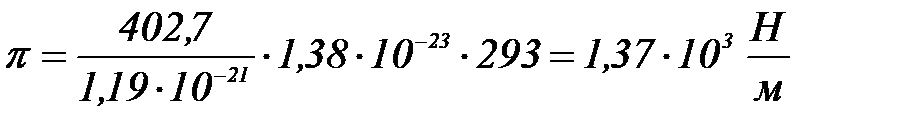 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|