
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Адсорбциялық тепе – теңдіктер.
СОӨ Ж №7
Адсорбциялық тепе – тең діктер.
Адсорбция шамасы адсорбент бетінің табиғ атына, адсорбат табиғ атына жә не концентрациясына (қ ысымына) температурағ а жыне т. б. байланысты. Берілген температурадағ ы адсорбцияның адсорцияланатын заттың кө лемдік фазадағ ы концентрациясына тә уелділігі адсорбция изотермасы деп аталады.
Шексіз сұ йытылғ ан ерітінділердің немесе газдар қ оспасынан адсорбция Генри заң ына бағ ынады:
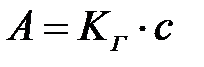 немесе
немесе 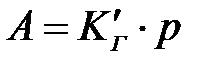
мұ ндағ ы: 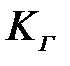 жә не
жә не 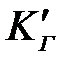 – Генри тұ рақ тылары; С – кө лемдік фазадағ ы адсорбат концентрациясы; р – адсорбаттың буының қ ысымы.
– Генри тұ рақ тылары; С – кө лемдік фазадағ ы адсорбат концентрациясы; р – адсорбаттың буының қ ысымы.
Жоғ арылау концентрациядардағ ы жә не тегіс беттегі дарамолекулалық адсорбция изотермасының аналитикалық ө рнегі Ленгмюр изотермасының тең деуі болып табылады:
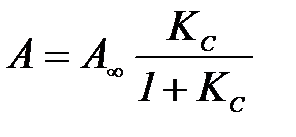 немесе
немесе 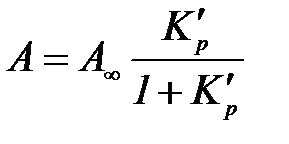
мұ ндағ ы: 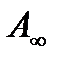 – шектік дарамолекулалық адсорбция – дара қ абат сыйымдылығ ы; К жә не
– шектік дарамолекулалық адсорбция – дара қ абат сыйымдылығ ы; К жә не 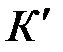 – адсорбциялық тепе – тең дік константалары, адсорбция энергиясын сипаттайды.
– адсорбциялық тепе – тең дік константалары, адсорбция энергиясын сипаттайды.
Будың жоғ ары қ ысымдарында адсорбция изотермасы Ленгмюрдің біріктірілген теориясының жалпы тең деуімен – БЭТ (Брунауэр, Эммет, Теллер) кө пмолекулалық адсорбция тең деуімен ө рнектеледі:
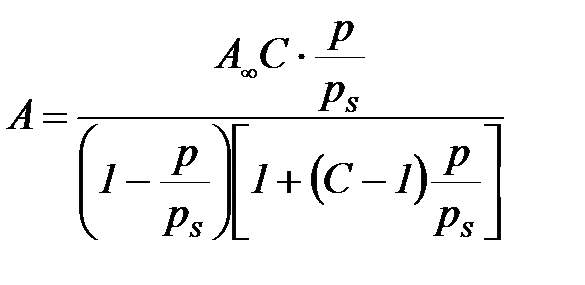
мұ ндағ ы: С – конденсирленген адсорбаттың адсорбент бетімен ә рекеттесу энергиясын сипаттайтын тұ рақ ты; 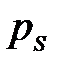 – адсорбаттың қ анық қ ан буынынң қ ысымы.
– адсорбаттың қ анық қ ан буынынң қ ысымы.
Ленгмюр жә не БЭТ тең деулері адсорбент, катализатордың жә не т. б. дисперстік жү йелердің меншіктік бетін анық тауда кең қ олданылады.
Меншікті беттің 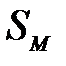 дарақ абат сыйымдылығ ымен байланысты:
дарақ абат сыйымдылығ ымен байланысты:
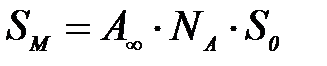
мұ ндағ ы: 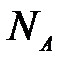 – Авогадро саны;
– Авогадро саны; 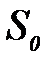 – қ анық қ ан адсорбциялық қ абатта адсорбаттың бір молекуласы алатын ауданы.
– қ анық қ ан адсорбциялық қ абатта адсорбаттың бір молекуласы алатын ауданы.
Ө тпелі кеуектері бар қ атты денелердегі (мезокеуекті адсорбенттер) адсорбцияны сипеттау ү шін Кельвиннің капиллярлық конденсация тең деуін қ олданады. Оның кө мегімен кеуектердің ө лшемін анық тауғ а болады. Егер денеде негізінен микрокеуектер болса, онда микрокеуектердің кө лемдік толтырылу теориясының тең деуі қ олданылады:
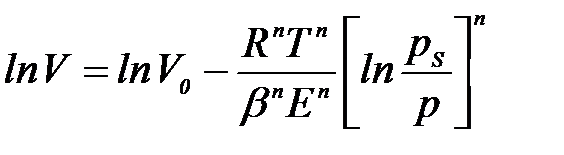
мұ ндағ ы: V – берілген қ ысымда толтырылғ ан кеуектер кө лемі; 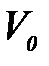 – адсорбенттегі кеуектердің жалпы кө лемі; b – адсорбат табиғ атын сипаттайтын аффин коэффициенті; Е – адсорбцияның сипаттамалық энергиясы; п – 1 – ден 6 – ғ а дейінгі бү тін сандар болатын дә реже кө рсеткіші.
– адсорбенттегі кеуектердің жалпы кө лемі; b – адсорбат табиғ атын сипаттайтын аффин коэффициенті; Е – адсорбцияның сипаттамалық энергиясы; п – 1 – ден 6 – ғ а дейінгі бү тін сандар болатын дә реже кө рсеткіші.
Адсорбцияның энергетикалық параметрлерін 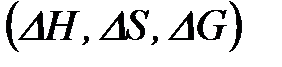 ә детте адсорбцияның температуралық тә уелділіктерінен есептейді. Мысалы, Клайперон – Клаузиус немесе Вент – Гофф тең деулерінен келесі изотераны
ә детте адсорбцияның температуралық тә уелділіктерінен есептейді. Мысалы, Клайперон – Клаузиус немесе Вент – Гофф тең деулерінен келесі изотераны 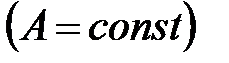 алуғ а болады:
алуғ а болады:
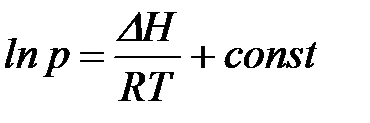
мұ ндағ ы: 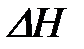 – адсорбция кезінде энтальпия ө згерісі.
– адсорбция кезінде энтальпия ө згерісі.
Осы тең деудің координаталарында тұ рғ ызылғ ан тә жірибелік тә уелділік бойынша (қ исаю бұ рышының тангенсі бойынша) (берілген А – да) берілген толтырылу дә ріжесіндегі адсорбция энтальпиясының дифференциалдық мольдік шамаларын анық тауғ а болады.
Адсорбцияның стандарттық Гиббс энергиясы 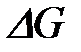 адсорбцтя тепе – тең дік константасымен К келесі қ атынас арқ ылы байланысады:
адсорбцтя тепе – тең дік константасымен К келесі қ атынас арқ ылы байланысады:
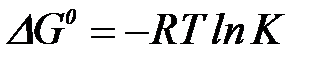
Стандарттық энтальпия мен Гиббс энергияларын біле отырып, адсорбция энропиясын оң ай есептеуге болады.
БАЗ – дың адсорбциялық қ абілеті жоғ ары болады, олар ү шін 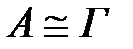 . Сондық тан БАЗ – ғ а қ атысты Гиббс жә не Генри тең деуін шешуге болады. ерітіндіде БАЗ – ң тө менгі концентрациядағ ы s – ң сызық тық изотермасын береді:
. Сондық тан БАЗ – ғ а қ атысты Гиббс жә не Генри тең деуін шешуге болады. ерітіндіде БАЗ – ң тө менгі концентрациядағ ы s – ң сызық тық изотермасын береді:
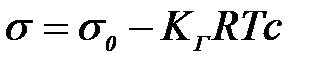
мұ ндағ ы: 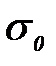 – еріткіштің беттік керілуі.
– еріткіштің беттік керілуі.
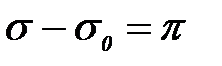 – беттік (екі ө лшемді) қ ысым десек,
– беттік (екі ө лшемді) қ ысым десек,
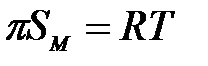
мұ ндағ ы: 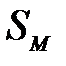 – 1 моль БАЗ таралғ ан бет.
– 1 моль БАЗ таралғ ан бет.
Гиббс жә не Ленгмюр тең деуін бірге шешу Шишковский тең деуін береді:
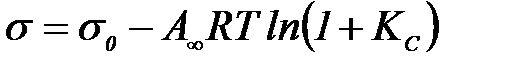
Екі ө лшемді газ тең деуі бұ л жағ дайда:
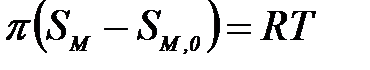
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|