∆x= 2RT/ NA •1 / 6πηr • t = RT/ NA• t / 3πηr (36)

Броундық қ озғ алысты жан-жақ ты зерттеген Перрен ө з тә жірибесінде алғ ан мә ліметтерге сү йеніп жә не математик Ланжевенің кө мегімен Авогадро санының ( N_A ) мә нін дә л анық тайды. Броундық қ озғ алыс тек коллоидты химияны, табиғ аттану ілімдерін дамытып қ ана қ оймастан, жалпы диалектикалық, материалистік кө зқ арастың дұ рыстығ ын, ғ ылымилығ ын дә лелдеді.

Диффузия дегеніміз жү йедегі молекулар, иондар немесе коллоидты бө лшектердің хаосты жылулық қ озғ алысының ә серінен олардың концентрациясының ө здігінен тең есу процесі. Яғ ни диффузия молекулалардың жылулық қ озғ алысының макроскопиялық кө рінісі, сол себепті температура жоғ арылағ ан сайын, диффузия да тез жү реді. Диффузия қ айтымсыз процесс, ол концентрацияның толық толық тең есуіне дейін жү реді, себебі бө лшектердің хаосты таралуы жү йенің максималды энтропиясына сә йкес келеді. 1885 жылдан бастап Нэрнст диффузияның пайда болу себебін осмостық қ ысыммен тү сіндірген?
Диффизия нә тижесінде массаның тасымалдануы жылу мен электрдің тасымалдану заң дылық тарына ұ қ сас. Осы ұ қ састық ты пайдалана отырып, 1855 жылы Фик диффузияның бірінші заң ын ұ сынды:
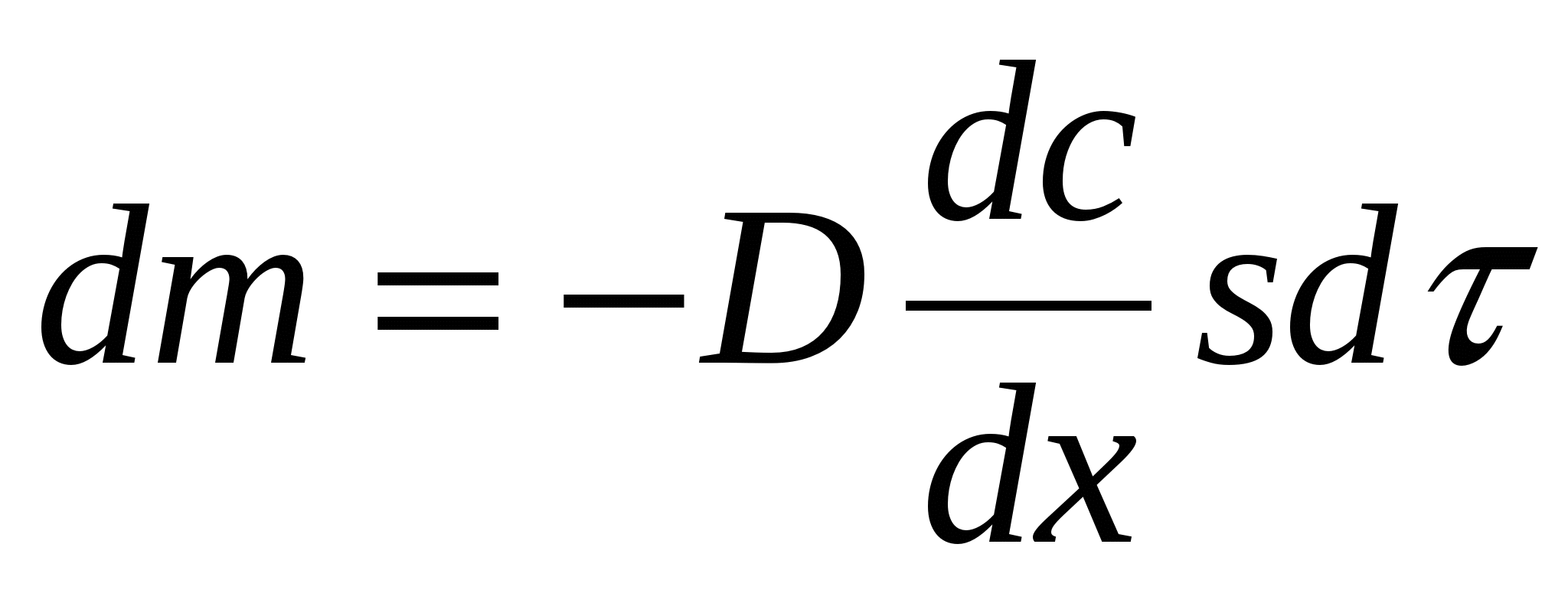(1)
Мұ ндағ ы: m – диффузияланғ ан зат мө лшері;
D – диффузияланатын бө лшектер жә не орта қ асиеттеріне тә уелді диффузия коэффициенті;
dc/ dx – концентрация градиенті;

s – диффузия ө тетін аудан;

τ – диффузия ұ зақ тығ ы;

Тең деудің оң бө лігіндегі минус таң басы dc/ dx туындысы теріс мә нге ие болатындық тан қ ойылып отыр, себебі х-тің мә ні жоғ арылағ ан сайын, концентрация c шамасы тө мендейді. (1) – ші тең деуден тө мендегідей тү рде де беруге болады.

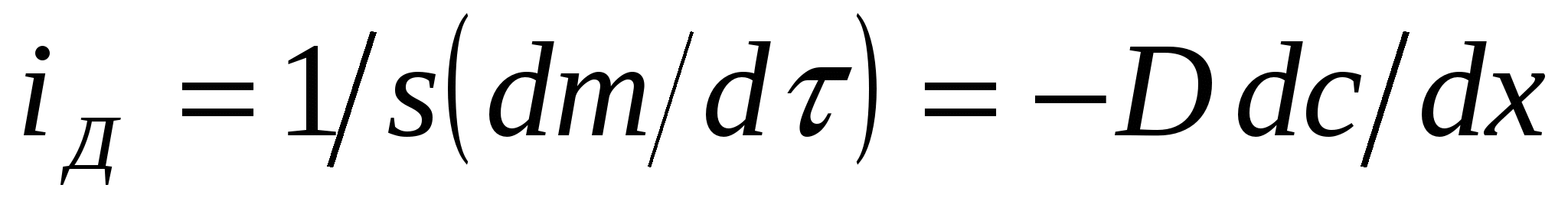(2)
і _д –диффузияның меншікті ағ ымы деп аталатын шама. Ол аудан бірлігіне тең кө лденең қ има арқ ылы уақ ыт бірлігінде диффузия нә тижесінде тасымалданатын зат мө лшерін сипаттайды.

Егер концентрация градиенті тұ рақ ты болса, диффузиялық ағ ын уақ ыт ө те келе ө згермей, жү йеде стационарлық диффузия процесі орнығ ады. Бұ л жағ дай ү шін мына тең деуді жазуғ а болады.

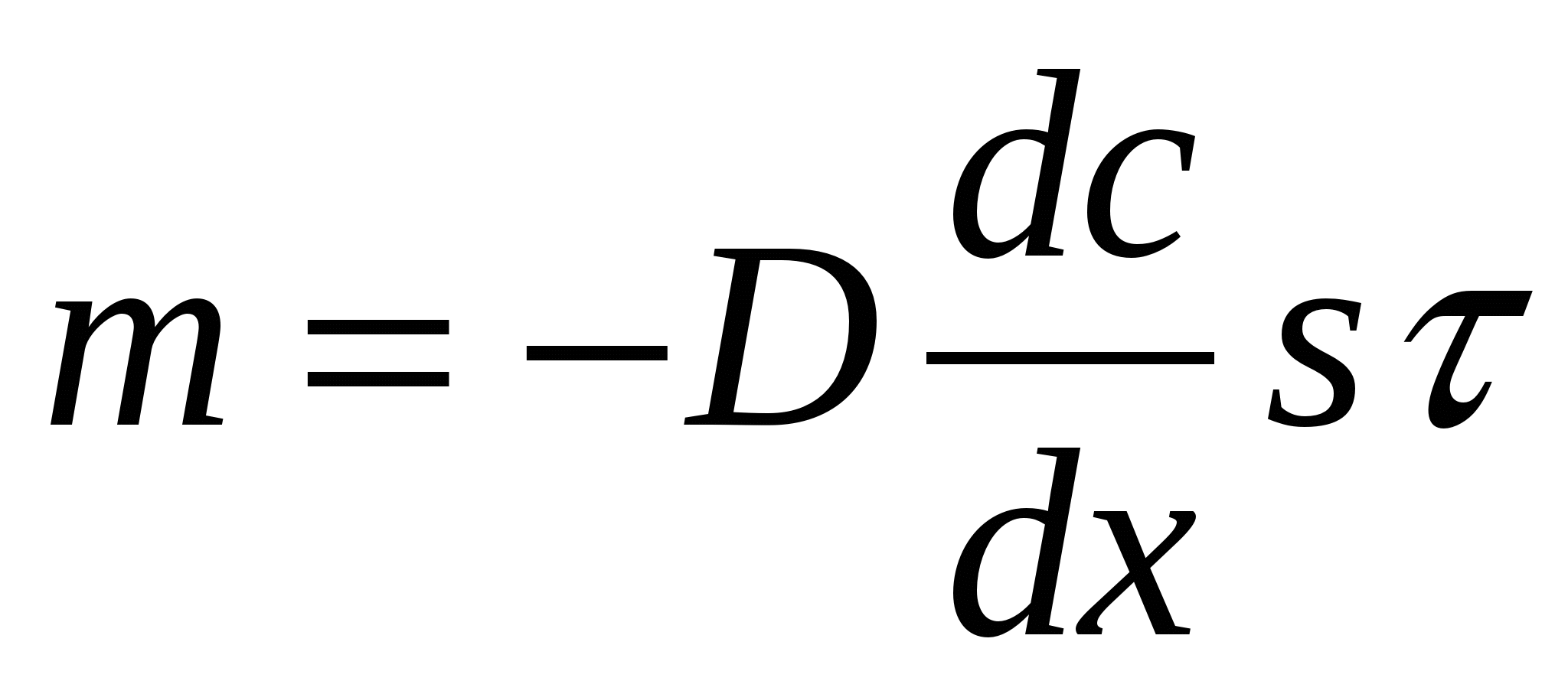
dc/dx=-1, s=1 жә не τ =1 деп алсақ,

m=D, яғ ни, концентрация градиенті 1-ге тең болғ ан жағ дайда диффузия коэффициенті уақ ыт бірлігінде аудан бірлігі арқ ылы диффузияланғ ан зат мө лшеріне тең, жә не ол см²/сек-пен ө лшенеді. Алайда диффузия ө те баяу жү ретіндіктен уақ ыт бірлігі ретінде секунд емес тә улік алынады.
1908 жылы Эйнштейн D диффузия коэффицентін Т жү йенің абсолютті температурасымен, η дисперсиялық орта тұ тқ ырлығ ымен жә не r дисперсті фаза бө лшегінің радиусымен байланыстыратын тең деуді қ орытып шығ арды.
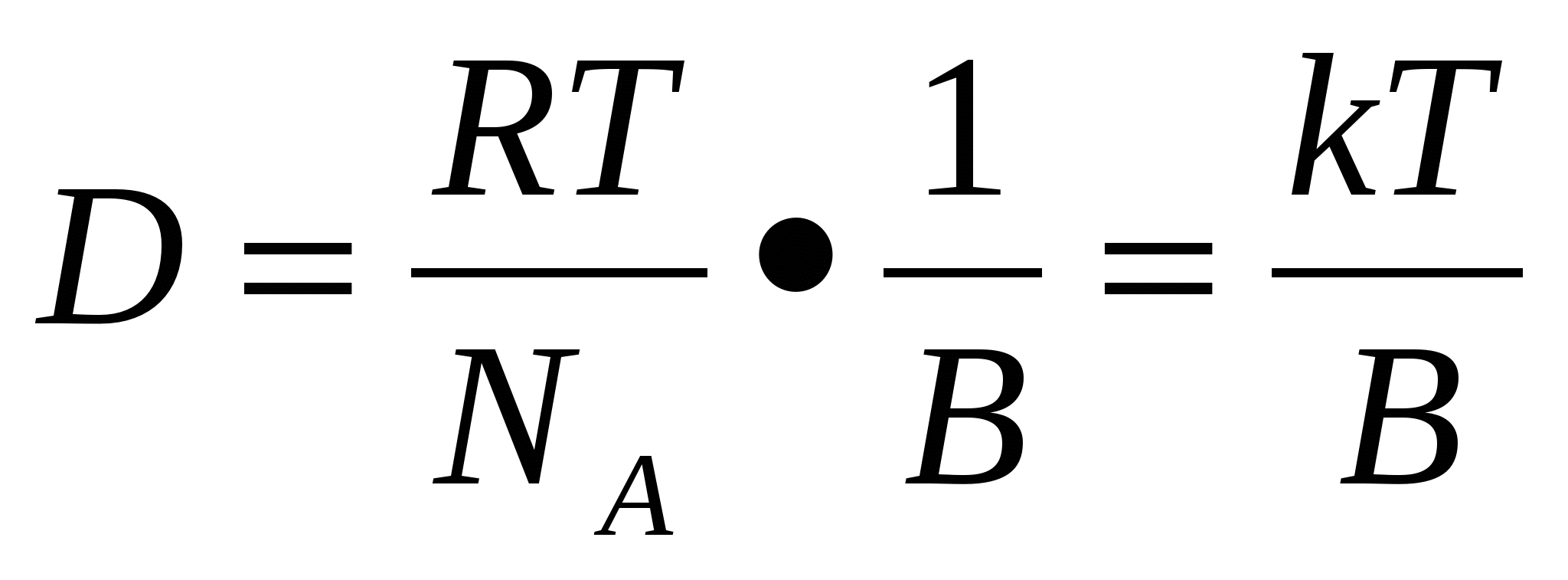Эйнштейн тең деуі

K= R / N_A – пропорционалдық коэффиценті

Формасы сфера тә різдіге ұ қ сас бө лшектер ү шін В = 6π η r тең болғ андық тан:

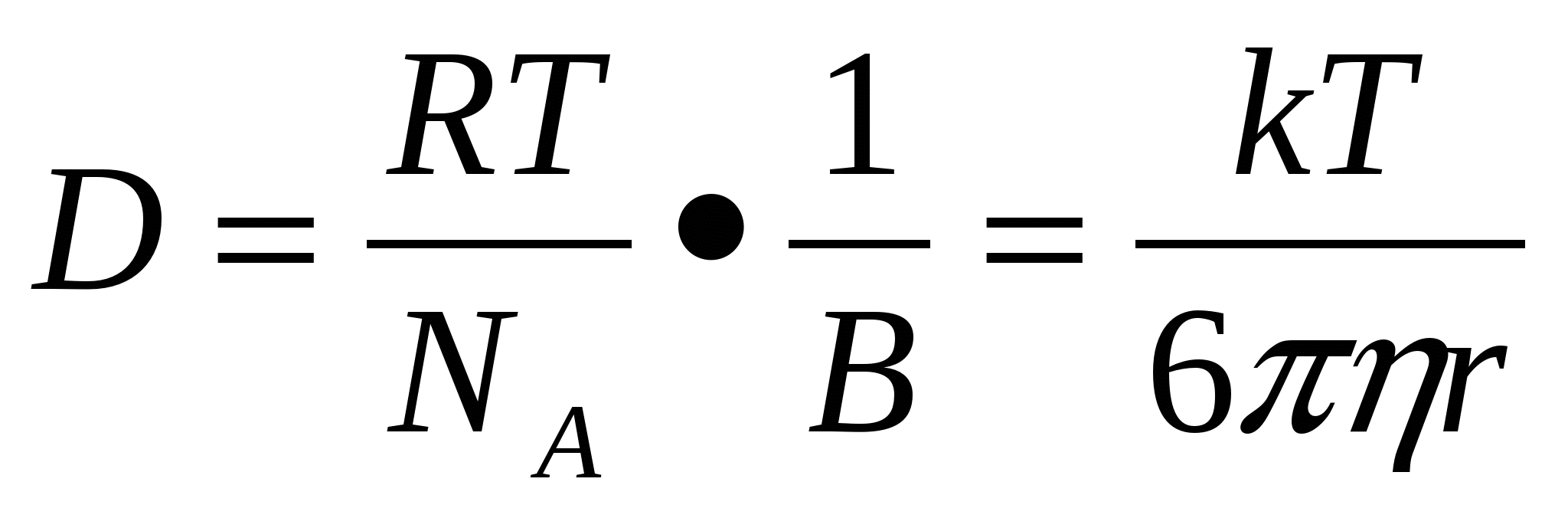
Мұ ндағ ы В- бө лшек жә не орта арасындағ ы ү йкеліс коэффициенті.
R – универсал газ тұ рақ тысы;

Т – абсолюттік температура;

N_A– Авагадро саны;

η – ортаның динамикалық тұ тқ ырлығ ы;

r – бө лшек радиусы;

π – осмостық қ ысым;

Тең деуден кө ріп отырғ анымыздай диффузия коэфициенті абсолютті температурағ а тура пропорционал, ал орта тұ тқ ырлығ ы мен бө лшек радиусына кері пропорционал. Коллоидтық бө лшектер ө лшемі қ арапайым молекулар ө лшемімен салыстырғ анда ө те ү лкен болғ андық тан, коллоидты жү йедегі диффузия коэффициенті тө мен болады.
Эйнштейн тең деуін пайдалана отырып, егер D, Т, η белгілі болса, 1 моль заттың массасын анық тай аламыз. Ол ү шін алдымен бө лшек радиусын есептеу керек.

r = kT / 6π η D

1 моль зат ү шін оның массасы келесі тең деумен анық талады

М = 4/3 π r³ρ N_A

ρ – ә детте белгілі дисперсті фаза тығ ыздығ ы.

Яғ ни диффузия коэфициентін ө лшеу арқ ылы (сан жағ ынан 1 моль зат массасына) тең заттың молекулалық массасын анық тауғ а болады.
Шынайы ерітіндідегі диффузияның ө ту себебі молекуланың жылулық қ озғ алысымен байланысты. Ал коллоидты жү йелердегі дисперсті фаза диффузиясының пайда болу себебі де, бө лшектердің броундық қ озғ алысымен тікелей байланысты. Броундық қ озғ алыс пен диффузия арасында байланыс болғ андық тан, ығ ысу проекциясының орташа квадраттық мә ні жә не диффузия коэффициенті D арасында да байланыс болу керек. Бұ л байланысты бір – бірінен тә уелсіз тү рде 1905 жылы Эйнштейн, ал 1906 жылы Смолуховский анық тады.

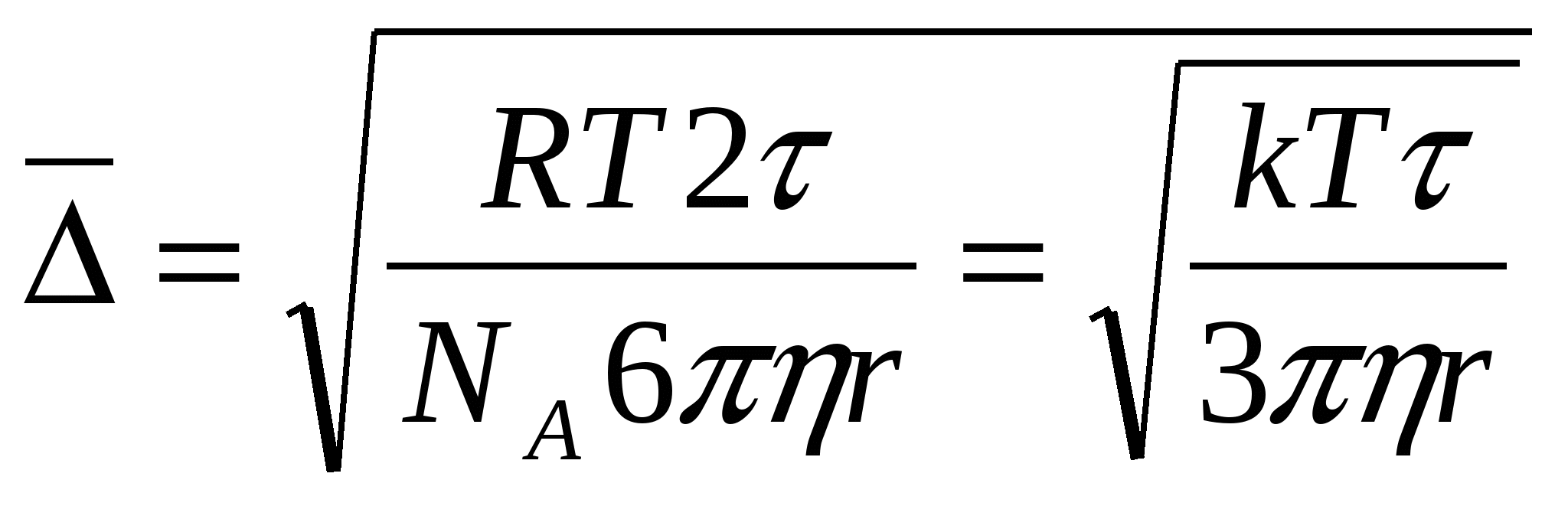
Эйнштейн – Смолуховский негізін қ алағ ан коллоидты жү йелердегі броундық қ озғ алыс теориясы дисперсті жү йе табиғ атын, осы жү йелердің молекулярлы – кинетикалық қ асиетінің ортақ тығ ын тү сіндіретін бірінші сандық теория болып табылады. Броундық қ озғ алысты зерттеу флуктуация теориясының пайда болуына жә не статистикалық физиканың дамуына ә серін тигізді. Флуктуация дегеніміз жү йенің айтарлық тай кіші кө лемінде қ андай да бір параметрдің тепе-тең орташа мә ннен ө те жоғ ары дә режеде ө здігінен (спонтанно) ауытқ уы. Флуктуацияларғ а физикалық шамалар (тығ ыздық, концентрация, т. б. ), биологиялық шамалар (ө сімі, тіршілік ұ зақ тығ ы, т. б. ), ә леуметтік–экономикалық шамалар (берілген жердегі халық тығ ыздығ ы, тауар бағ асы) ұ шырауы мү мкін. Флуктуацияның жалпы теориясының негізін 1902 жылы американ ғ алымы Гиббс қ алады.

Дисперсті фазаның бө лшектері молекулалық -кинетикалық қ озғ алыс салдарынан кездейсоқ қ озғ алыстарғ а да душар болады. Алайда берілген кө лемдегі бө лшектер концентрациясы ә р тү рлі болса, мә селен, ыдыстың тү біндегі бө лшектер концентрациясы оның бетіндегіден артық болса, онда осы бө лшектердің тө меннен жоғ арығ а қ арай қ озғ алуынан гө рі керісінше жоғ арыдан тө менге қ арай ауысуы артық болатыны анық. Ә рине, мұ ндай қ озғ алысты ауысулар берілген кө лемдегі концентрация мә ні тең елгенше жү реді, ал басқ а қ озғ алыстар тоқ таусыз жалғ асады.

Иондардың, молекулалардың немесе коллоидты бө лшектердің ретсіз жылулық қ озғ алыс ( коллоидты системалар ү шін броундық қ озғ алыс) кезіндегі концентрацияны тең естіру бағ ытында ө здігінен жү ретін процесін диффузия деп атайды. Демек, диффузия ө здігінен жү ретін процесс ретінде барлық дисперсті системалар ү шін, газдарғ а арналғ ан Фик заң ына бағ ынады. Фиктің бірінші заң ына байланысты диффузия жылдамдығ ы ө зі диффузияланатын аудан мен концентрациялық градиентке тура пропорционалды:

dm/dt = − DS dC/dx

Мұ ндағ ы dm – диффузияланғ ан зат массасы; dt – шексіз аз уақ ыт; S - берілген зат диффузияланғ ан аудан; dC/dx − концентрация градиенті немесе концентрация кемуі; dC − концентрция; dx − концентрациясы кеміген бө лік; D − диффуізия коэффициенті, ол ә рбір дисперсті системаның диффузиялану қ абілетін сипаттайды. Бұ л коэффициент концентрация градиенті 1-ге тең болғ анда бір шаршы сантиметр ауданнан 1 сек-та диффузияланып ө ткен масса мө лшерін кө рсетеді. Егер диффузия процесі кезінде диффузия коэффициенті ө згеретін болса, онда оғ ан орай концентрция градиенті де ө згереді. Олай болса уақ ытқ а байланысты концентрация ө згерісінің жылдамдығ ын, яғ ни dC/dt туындысын анық тау керек. Ол Фиктің екінші заң ын ө рнектейтін тең деумен анық талады:

dC/dt = Dd²C /dx²

Фиктің екі заң ын қ олдану кезіндегі негізгі қ иындық кө п уақ ытқ а дейін диффузия коэффициентінің мә нін табу болып келеді. Алайда бұ л коэффициентті анық тау қ иындығ ы Эйнштейн броундық қ озғ алысты зерттегенде оны (1) тең деудегі орташа жылжумен байланыстырғ алы жең ілденді. Эйнштейн сұ йық қ а арналғ ан Стокс заң ын пайдаланып, диффузия коэффициентінің дисперсті ортаның тұ тқ ырлығ ы мен бө лшек радиусына тә уелділігін анық тады. Қ азір коллоидты ерітіндідегі бө лшектің ө лшемін анық таудағ ы диффузиялық ә діс бірден-бір нақ тылы нә тиже беруде.

Коллоидты системадағ ы броундық қ озғ алыс пен диффузияны зерттеу дисперсті системаның табиғ атын терең ірек тү сінуге кө мектесіп, осы система мен молекулалық дисперсті системалар арасындағ ы молекулалық -кинетикалық орта қ асиеттерін анық тайды. Сө йтіп, бұ лар молекулалардың бар екенін оның материялығ ын айқ ындаумен қ атар, табиғ аттану ілімін материалистік тұ рғ ыдан тү сінуге ө з септігін тигізеді.

Броундық қ озғ алысты онан ә рі зерттеу флуктуация теориясы деп аталатын жаң а бағ ыттың пайда болуына ә келеді. Флуктуация деп тығ ыздық тың, концентрацияның немесе системадағ ы микрокө лемнің орташа мә нінен оның параметрлерінің ө здігінен ауытқ уын айтады. Мысалы, Сведберг флуктуация қ ұ былысын байқ ау кезінде, алтын золіндегі 1000 ммк³-де орналасқ ан коллоидты бө лшекті (алтынды) санайды. Ондағ ы бө лшектің орташа саны ө згеріп отырғ ан. Диффузия да, флуктуация да жылулық қ озғ алыстың нә тижесінен болғ анымен, олар біріне-бірі кері қ ұ былыс екен. Егер диффузия термодинамиканың екінші заң ына орай кез келген ө здігінен жү ретін процесс кезінде қ айтымсыз болса, онда бұ ғ ан кері жү ретін флуктуация қ ұ былысы термодинамика екінші заң ының статистикалық сипатын кө рсетеді, яғ ни оны жекелеген бө лшектерге немесе олардың аз санына қ олдануғ а болмайды.

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒