мұндағы D1 және D2 – бірінші және екінші зольдің дисперстік дәрежелері.

мұ ндағ ы D1 жә не D2 – бірінші жә не екінші зольдің дисперстік дә режелері.

Демек, коллоидты ерітінділердің осмостық қ ысымы, олардағ ы бө лшек радиусының кубына кері пропорционалды да, дисперстік дә режесінің кубына тура пропорционалды екен.

Седиментация

Диффузияны қ арастырғ ан кезде біз жү йеге гравитациялық ө рістің (тартылыс кү ші) ә серін есепке алғ ан жоқ пыз. Массасы айтарлық тай ү лкен бө лшектерге гравитациялық ө ріс ә сер ететіндіктен олар тұ нбағ а тү седі, тұ нады немесе седиментацияланады. Микрогетерогенді жү йелер-эмульсиялар, суспензиялар, газ эмульсиялары, аэрозольдерде броундық қ озғ алыс болмайтындық тан, седиментация немесе оғ ан қ арама қ арсы процесс - қ алқ ып шығ у жү реді. Осының нә тижесінде жү йеде бө лшектер биіктік бойынша белгілі-бір тепе-тең дік таралады немесе, бө лшектер ауыр болса, олар тұ нбағ а тү седі. Дисперсті жү йенің кө лем ішінде бө лшектердің біркелкі таралуын қ амтамасыз ету қ абілеті жү йенің седиментациялық немесе кинетикалық тұ рақ тылығ ы деп аталады. Яғ ни седиментациялық тұ рақ тылық немесе тұ рақ сыздық туралы айту тек босдисперсті жү йелерді қ арастырғ анда ғ ана орынды болады, себебі, ә р бө лшек еркін жә не жылулық қ озғ алыста болады.

Ірі дисперсті жү йелер (шаң, тозаң, немесе судағ ы қ ұ м суспензиясы) седиментациялық тұ рақ сыз жә не тұ нбағ а тү седі, себебі олардың бө лшектері ауыр болғ андық тан оларғ а жылулық, яғ ни броундық қ озғ алыс тә н емес. Жоғ ары дисперсті жү йелер (газдар, шынайы ерітінділер) жоғ ары кинетикалық тұ рақ тылық қ а ие, себебі оларғ а жылулық қ озғ алыс жә не диффузияғ а қ абілеттілік тә н. Коллоидты жү йелер (аэрозольдер, лиозольдер) тұ рақ тылығ ы бойынша екеуінің арасынан орын алады.

Диффузияның немесе седиментацияның дисперсті жү йенің кинетикалық тұ рақ тылығ ына қ алай ә сер ететінін қ арастыру ү шін диффузия ағ ыны жә не оғ ан қ арсы бағ ытталғ ан седиментация ағ ын салыстыруғ а болады i_D→ i_c. Меншікті диффузиялық ағ ын мына тең деумен анық талады.

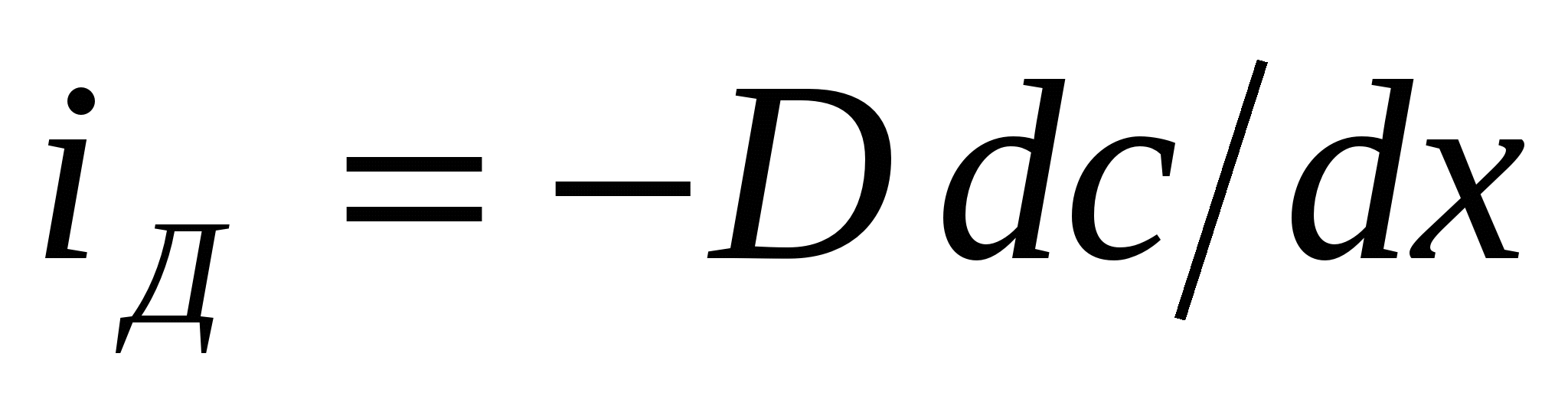(1)

Тұ рақ ты жылдамдық пен тұ натын бір бө лшек ү шін ү йкеліс кү ші Вu ауырлық кү шіне (қ озғ алтқ ыш кү шке) mg тең tекенін ескерсек, онда меншікті седиментациялық ағ ын тө мендегі тең деумен ө рнектеледі.

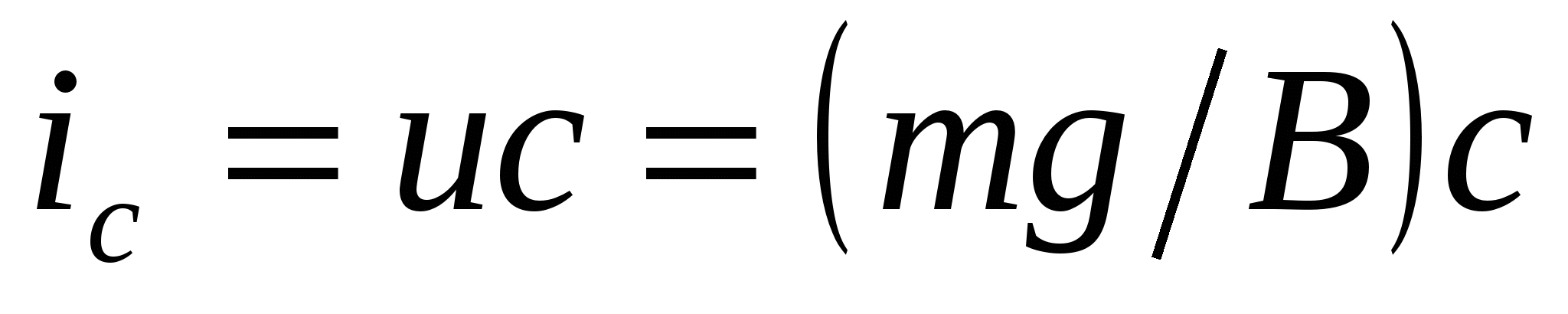(2)

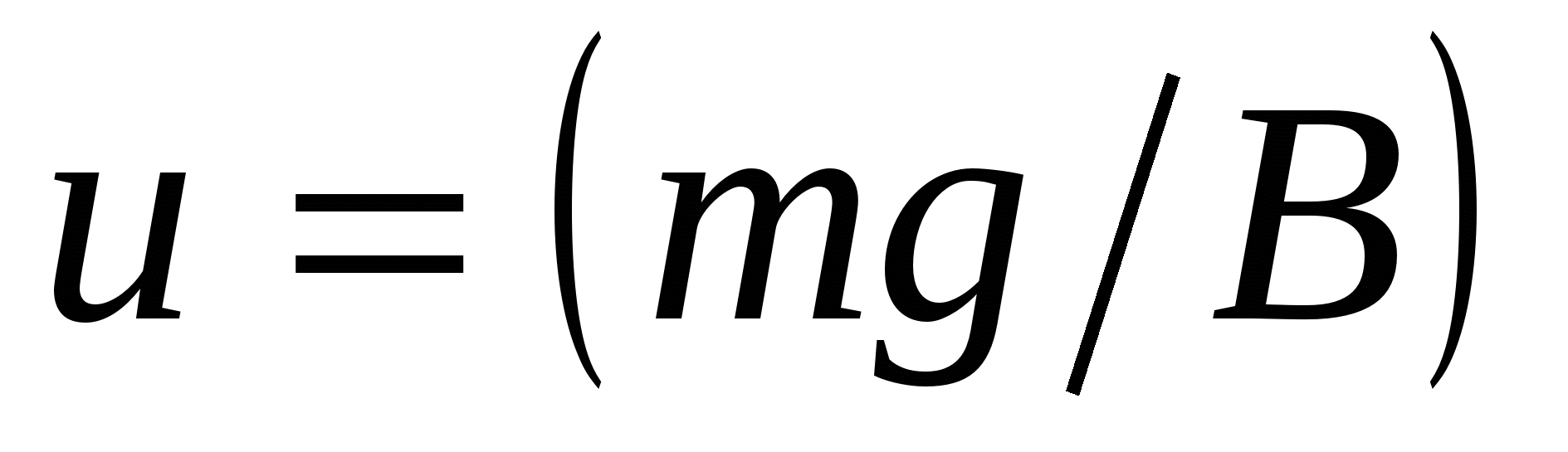
u–седиментацияжылдамдығ ы;
с–концентрация
m–бө лшектің тиімді массасы

B – коллоидты бө лшек пен диспесті орта аралығ ындағ ы ү йкеліс коэффициенті
g–еркін қ ұ лау ү деуі

Екі тең деуді бір-біріне бө лсек, жә не 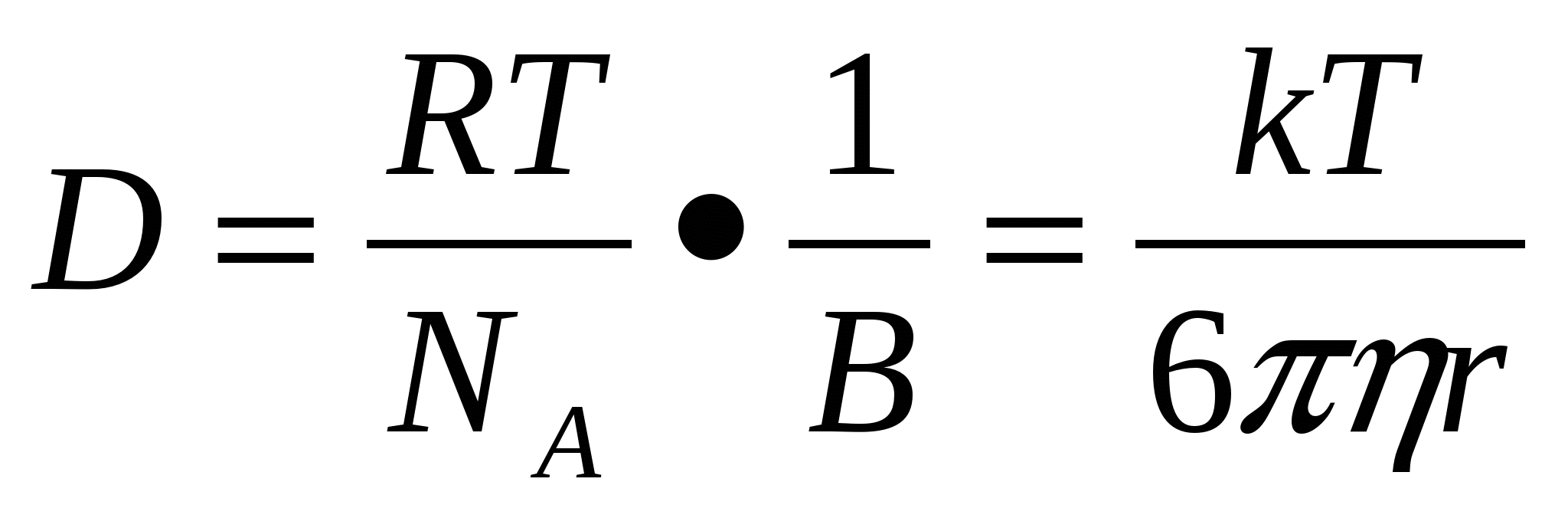екендігін ескерсек,

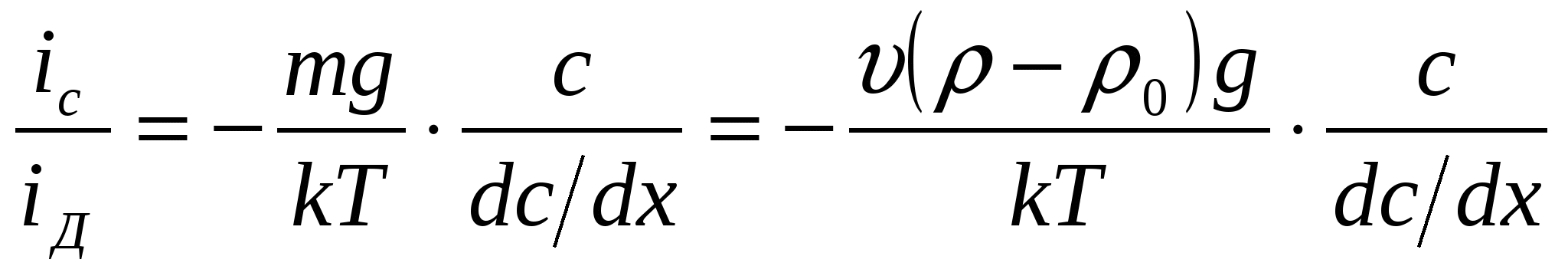(3)

υ – бө лшек кө лемі;

ρ, ρ – дисперсті фаза мен дисперсті орта тығ ыздық тары

i_С/ i_Д›› 1 болса, тек седиментация процесін есепке аламыз (ө теді деп есептейміз);

i_С/ i_Д ‹‹ 1 болса, тек диффузия процесін есепке аламыз;

i_С/ i_Д ≈ 1, яғ ни i_С≈ i_Д болса, екі процесті де есепке алу қ ажет. Бұ л жағ дайда дисперсті фаза бө лшектері жү йеде биіктік бойынша белгілі-бір тә ртіппен таралады.

(3) –ші тең деуден мынадай қ орытынды шығ аруғ а болады, алдын-ала араластыру нә тижесінде дисперсті фазасы кө лемде біркелкі таралғ ан жү йенің тұ рақ тылығ ын қ арастыратын болсақ, алғ ашқ ы уақ ытта ә рқ ашан седиментация басым болады, себебі, алғ ашында dc/dx=0. Алайда уақ ыт ө ткен сайын заттың жү йеде біркелкі таралуы бұ зылып, dc/dx туындысының мә ні арта береді. Массатасымалы i_С/ i_Д ≈ 1, яғ ни i_С≈ i_Д болғ анша жә не жү йеде тепе-тең дік орнағ анша жалғ асады. Концентрация градиенті биіктік бойынша ө згеретінін ескерсек, х- ті h-қ а ө згертіп, (3) –ші тең деуді былайша жазуғ а болады

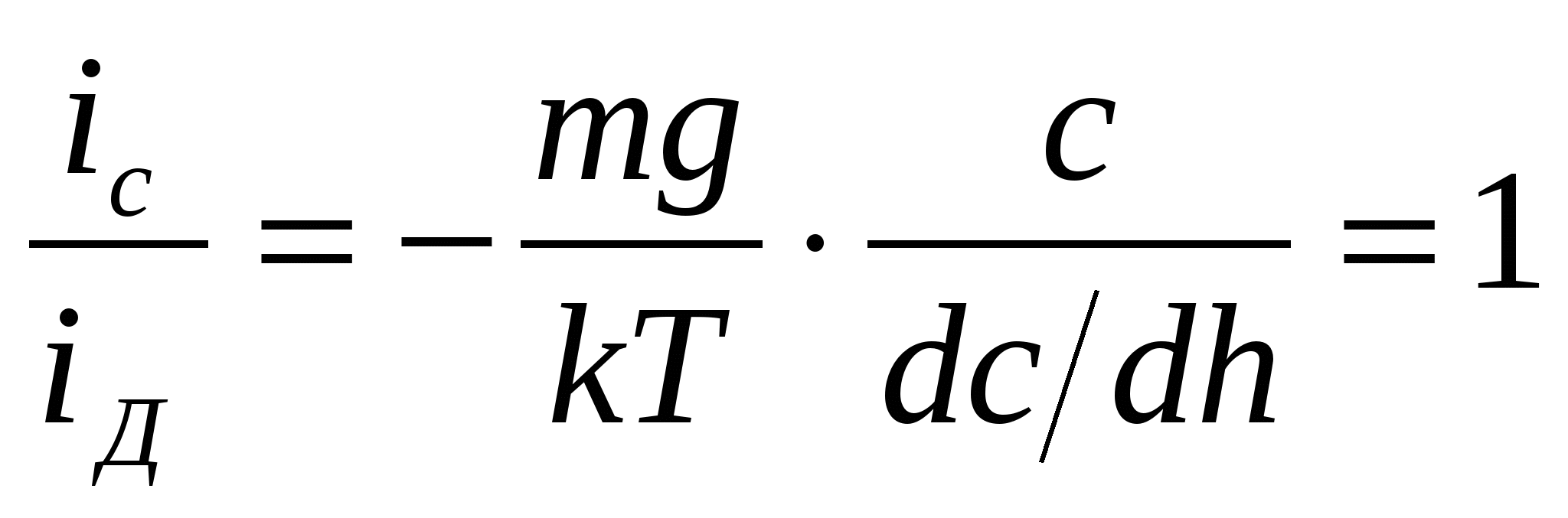(4)

Осы тең деуді былайша да жазуғ а болады.
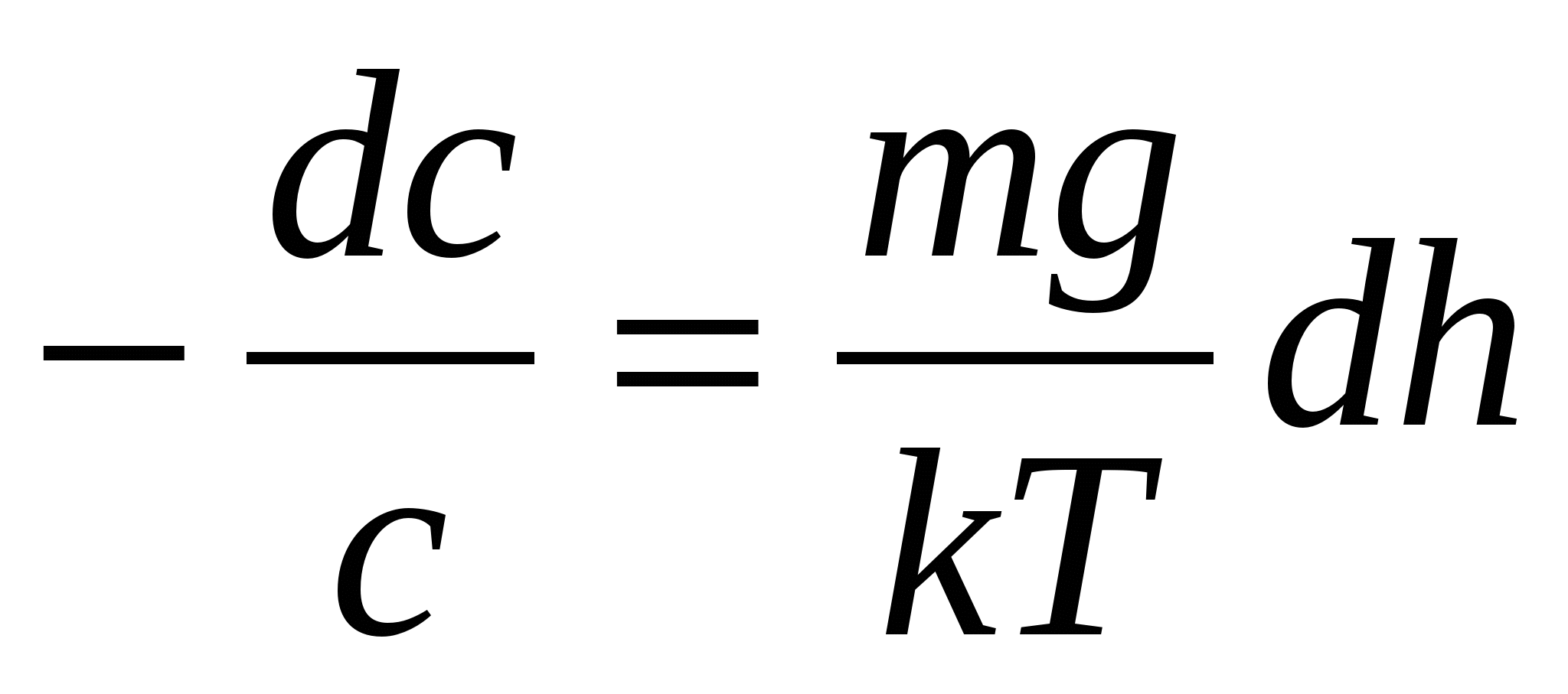(5)

с₀-ден с_h- қ а дейін, сә йкесінше 0-ден h-қ а дейін интегралдап мына тең деуді аламыз.

(6) немесе

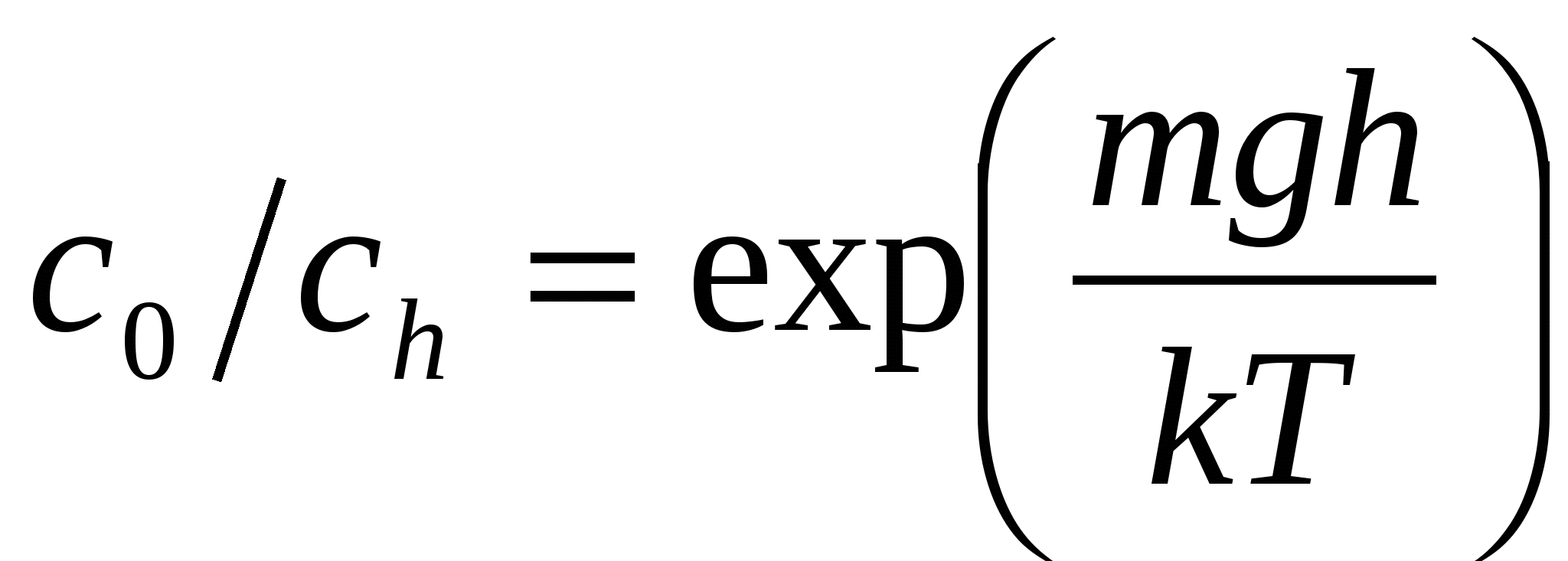(7)

Егер (6) –шы тең деудегі с орнына р қ ойсақ, белгілі барометрлік формуланы аламыз.

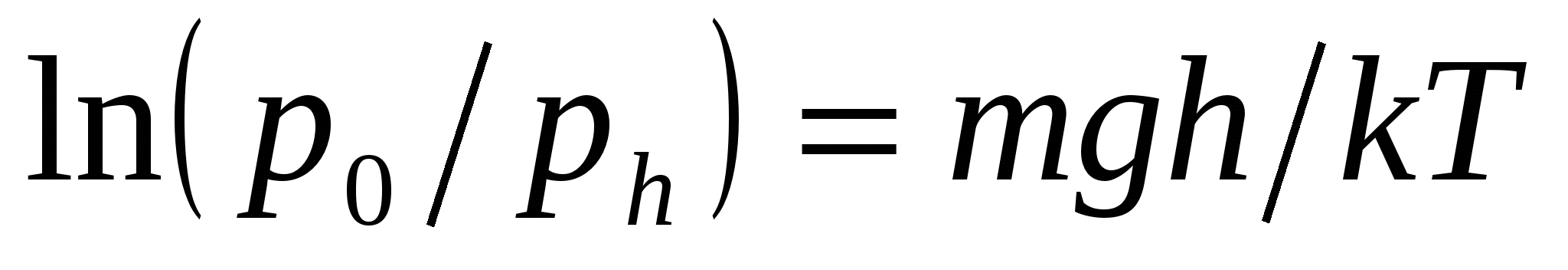(8)

Биіктік бойынша газ молекулаларының таралуы осы гипсометриялық заң ғ а(8)бағ ынады.

Дисперсті фаза концентрациясы с сандық концентрацияғ а ν пропорционал болғ андық тан, бұ л тең деуді былай етіп те кө рсетуге болады.

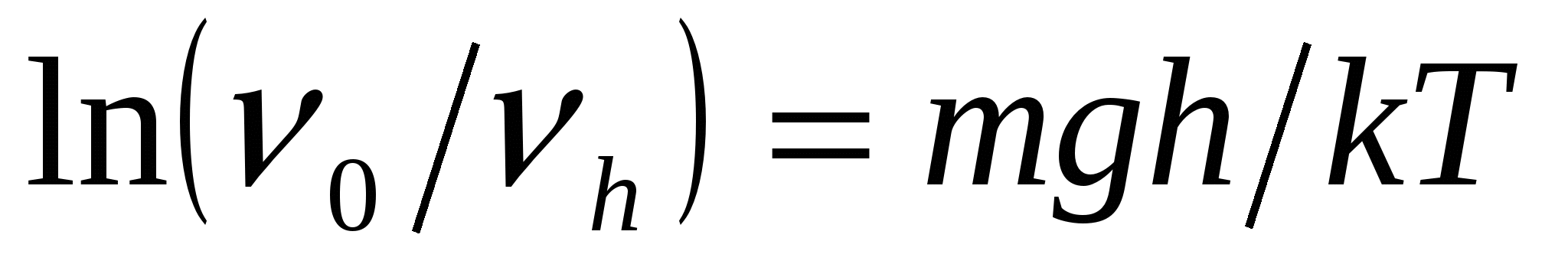(9)
Бұ дан 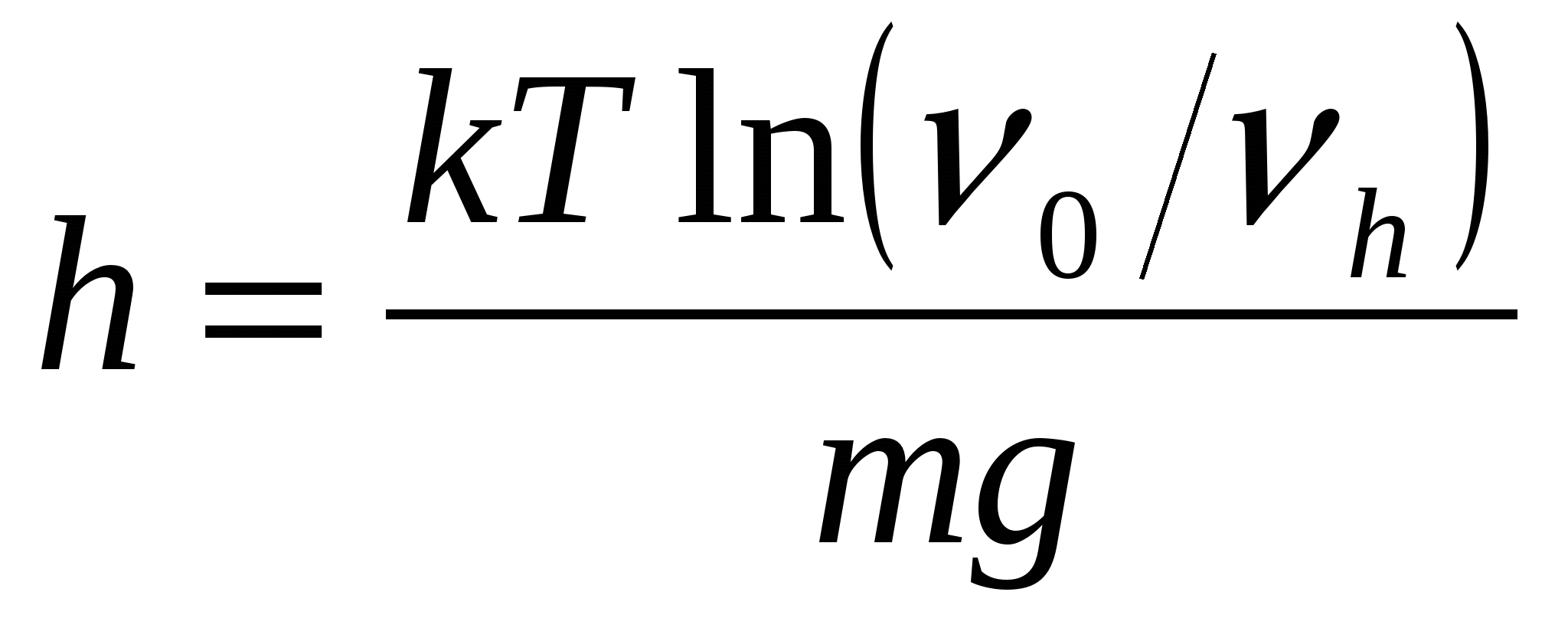(10)

Бұ л тең деу арқ ылы кез-келген босдисперсті жү йе ү шін h мә нін есептеп табуғ а болады. h дегеніміз сандық концентрация (немесе салмақ тық концентрация) ν ₀ден ν _h-қ а дейін немесе ν ₀/ ν _hесе тө мендейтіндей биіктік. Мысалы концентрация қ андай биіктікте екі есе азаятынын білгіміз келсе, ν ₀/ ν _h=2 деп алып h мә нін есептеуге болады.

Жү йеде бө лшектердің тепе-тең таралуына мынадай факторлар кедергі келтіруі мү мкін: болмашы соқ қ ы, шайқ ау, зольдің ә р учаскесінде температураның біркелкі болмауы. Мысалы жоғ арыдисперсті золь температурасы 1 сағ ат ішінде 0, 001⁰С-ге ауытқ уының ө зі, алтынның жоғ арыдисперсті золінде мү лдем седиментацияны болдырмай тастайды.

Қ алай дегенмен, жү йеде бө лшектер таралуының тепе-тең кү йі орнағ аннан кейін лиозольдер ү шін гипсометриялық заң дә л сақ талады.
Мұ ны гуммигут суспензиясымен тә жірибе жасағ ан Перрен жә не алтын золімен тә жірибе жасағ ан Вестгрен N_A мә нін анық тай отырып, дә лелдеді.

Ауырлық кү шінің ә серінен бө лшектердің тұ нбағ а тү су процесін седиментация деп атайды. Тұ нбағ а тү су жылдамдығ ы бө лшектердің кө леміне, тығ ыздығ ына, ортағ а, сұ йық тық қ а жә не ауырлық кү шінің уақ ытына тә уелді. Стокс заң ы бойынша қ озғ алу кезінде бө лшектер сфералық тұ тқ ыр ортада қ арсылық кү шін сезеді, ол тең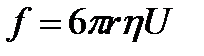

мұ ндағ ы, 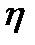- орта тұ тқ ырлығ ы, 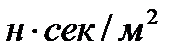, r – бө лшек радиусы, м.

U – тұ нба тү су жылдамдығ ы, м/сек, Басқ а жақ тан бө лшекке кү ш ә сер етеді.

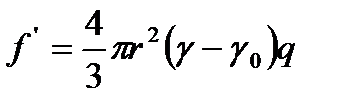
мұ ндағ ы, 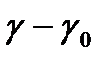- дисперсті ортадағ ы бө лшектер тығ ыздығ ының айырымы, кг/м³

q – ауырлық кү шінің жылдамдығ ы, м/сек²

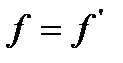тең болғ анда жә не тұ рақ ты температурада тұ нбағ а тұ рақ ты тү су жылдамдығ ына жетеді

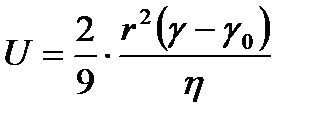
Бө лшектердің тұ нбағ а тү су жылдамдығ ын бө ліп алып, оның радиусын есептейміз.

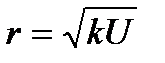
мұ ндағ ы, 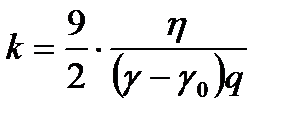берілген суспензияғ а тұ рақ ты шама.

Тұ нбағ а тү су жылдамдығ ы бө лшек радиусына тә уелді. Мысалы, саз бө лшегінің 1∙ 10^{-5 м радиусты 1см-ге 43сек. уақ ыт ө теді, ал 2∙ 10-6 м радиуста 17 минут, 1∙ 10-8}м радиуста – 500 кү н кетеді. Егер бө лшек 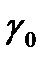тығ ыздық та қ озғ алатын болса, онда оның қ озғ алысы тө меннен жоғ арығ а, ал зат бө лшегінің тығ ыздығ ы 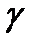немесе орта тығ ыздығ ына тә уелді болады.

Суспензияда 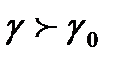жә не бө лшектер тұ нбағ а тү седі, эмульсияда 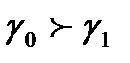сондық тан бө лшектер қ алқ ып шығ ады. Мысалы, судағ ы саздың тұ нуы, сү ттегі қ аймақ тың тү зілуі жатады.

Бө лшектердің толық тү суі ауырлық кү шінің ә серінен болмайды, ө йткені оғ ан қ арсы броундық қ озғ алыс ә рекет етеді, яғ ни ол бө лшектерді ерітіндінің барлық кө леміне тең бө луге тырысады. Броун қ озғ алысының ә сері кө п ә сер етеді, егер бө лшектің кө лемі кішкентай болғ ан жағ дайда.

Егер бө лшектердің негізгі бө лігі қ ысқ а мерзімде тұ нса, онда ондай жү йені кинетикалық тұ рақ сыз деп атайды, ал егер бө лшектер ұ зақ мерзім ішінде тепе-тең бө лінсе, оны кинетикалық тұ рақ ты жү йе деп атайды.

Суспензия мен эмульсиялар – бұ лар кинетикалық тұ рақ сыз жү йе, ал коллоидты жү йе мен ерітін ділер жоғ арғ ы молекулярлы – кинетикалық тұ рақ ты.

Седиментация процесі кинетикалық тұ рақ сыз жү йе – суспензияғ а тә н.

Кинетикалық тұ рақ ты тұ нуды қ арапайым жағ дайда тү зуге болады, егер жердің ауырлық кү шінің центрге тартқ ыш кү ші жоғ ары болса. Центрифуга арқ ылы центрге тартқ ыш кү шті алуғ а болады, 10⁵ есе артық ауырлық кү ші бар жә не бө лшектің тұ ну жылдамдығ ын сонша есе жылдамдатуғ а болады. Центрифугат қ олдану арқ ылы коллоид пен жоғ арғ ы молекулярлы ерітінділерге седиментация жү ргізуге болады.

Седиментациялық анализ тұ нғ ан бө лшектердің жылдамдығ ын ө лшеуге негізделген. Тә жірибеде кездесетін суспензия қ арапайым полидисперсті, онда ә ртү рлі кө лемдегі бө лшектер болады. Седиментация процесі ө ндірісте қ олданылады. Тұ ну жылдамдығ ын бақ ылау бө лшектердің салмақ тық, сандық анық тауғ а ә ртү рлі кө лемдегі полидисперсті жү йедегі мү мкіндік береді. Бұ л принципке сү т сепараторының жұ мысы негізделген, яғ ни сү ттен қ аймақ ты айыру процесі. Сепарация процесі (айыру) центрлік тартқ ыш кү ш арқ ылы тез ө теді, сү ттің сол қ алпында тұ рғ анына қ арағ анда.

Седиментацияны қ олдану центрге тартқ ыш ө ріс арқ ылы жоғ арғ ы молекулярлы ерітінділердегі бө лшектердің кө лемін анық тайды.

Сұ йық не газды ортадағ ы ұ нтақ талғ ан заттың бө лшектері қ арама-қ арсы бағ ытталғ ан екі кү штің ә серінде болады. Олардың біріншісі бө лшекті тө мен тартып, тұ нбағ а немесе шө гіндіге тү сіруге бағ ытталғ ан ауырлық кү ш, ал келесі бө лшектерді берілген кө лемде біркелкі таратуғ а ұ мтылғ ан, яғ ни бө лшек концентрациясы мол жақ тан, аз жақ қ а қ арай ауысуына ә сер ететін ө здігінен жү ретін диффузиялық кү ш. Дисперстік системағ а ә сер ететін ауырлық жә не диффузиялық кү штің қ айсысының басым болуына байланысты оның кү ші анық талады: ауырлық кү ші артық болса, ондайда дисперсті системаның бө лшектері кө бірек шө геді, ал диффузиялық кү ш басым болса, онда дисперстік системадағ ы бө лшектер тұ нбағ а тү спей жү згін тү рінде болады. Осы айтылғ андарғ а орай, дисперсті фазаның система кө лемінде біркелкі таралып, тұ рақ ты кү йде болуын седиментациялық немесе кинетикалық тұ рақ тылық деп атайды, ал ауырлық кү ші ә серінен бө лшектердің тұ нбағ а тү су процесі седиментация деп аталады. Системадағ ы бө лшектердің тұ нбағ а тү су жылдамдығ ы осы бө лшектердің ө лшеміне, дисперстік ортаның тұ тқ ырлығ ына жә не бө лшек тығ ыздық тарына тә уелді:

υ = 2/3 · r² (d-d) g / η

мұ ндағ ы υ - бө лшектердің тұ нбағ а тү су жылдамдығ ы; r- бө лшек радиусы; d жә не d₀- дисперсті бө лшек пен дисперстік ортаның тығ ыздық тары; η - дисперстік ортаның тұ тқ ырлығ ы; g- еркін тү су ү деуі.

Дисперсті фаза ө те ұ сақ болса диффузия жылдамдығ ы ү лкен болады. Ал олар іріленген сайын диффузия жылдамдығ ы баяулайды. Бө лшектің радиусы 2 нм-ден ү лкен болса, броундық қ озғ алыс байқ алмайды, демек олардың диффузиялық қ абілеті нө лге тең. Мұ нда ауырлық кү ші диффузиялық кү штен басым.

Егер дисперсті системадағ ы ауырлық кү ші мен диффузия кү ші ө зара тең болса, онда седиментация мен диффузия жылдамдық тарының тепе-тең дігімен сипатталатын седиментациялық тепе-тең дік деп аталатын кү й орнайды. Мұ ндайда берілген дисперсті системаның бірлік ө лшемі арқ ылы ауырлық кү шінің ә серінен тө менқ арай қ анша бө лшек ө тсе, диффузиялық кү ш ық палынан жоғ арығ а қ арай сонша бө лшек ө теді. Осындай седиментациялық тепе-тең дік коллоидты системағ а ғ ана емес, молекулалық -дисперстік системалар ү шін де тә н қ ұ былыс. Сондай-ақ бұ л тепе-тең дік системадағ ы бө лшек концентрацияларының уақ ыт ө ткен сайын баяу болса да тө меннен жоғ арығ а қ арай кеми беретіндігімен де сипатталады. Сұ йық бағ анасындағ ы бө лшектер ө зінің ө лшеміне сә йкес ә ртү рлі биіктікте, айталық ірілері тө мен, ал ұ сақ тары жоғ ары орналасады екен. Бұ л қ ұ былысты сипаттау ү шін Лапластың гипсометриялық немесе барометрлік заң ын коллоидты системағ а пайдалануғ а болады: золь бағ анасының биіктігін арифметикалық прогрессияда кө бейткенде, бө лшек концентрациясы геометриялық прогрессияда кемиді. Бұ л заң дылық ты математикалық тұ рғ ыдан ө рнектесек:

h = RT ln C₁/С₂ / M·g

мұ ндағ ы C₁– берілген биіктіктегі дисперсті системаның концентрациясы; С₂– осы системаның h биіктіктегі концентрациясы; h- ө лшентін бағ - ө лшентін бағ ана биіктігі; М- заттың салщыстырмалы молекулалық массасы; g- еркін тү су ү деуі. Ә уелде Лапластың гипсометриялық заң ы газ тә різді жә не молекулалық -дисперстік системаларғ а арналып тұ жырымдалғ ан болатын. Бертін келе Перрен оны коллоидтық -дисперстік, тіпті ірі дисперстік системаларғ а қ олданды. Осы мақ сатпен Перрен радиустері ә ртү рлі кө птеген шариктер ә зірлеп, оларды ө лшеміне орай сұ рыптап, дисперстік ортаны да белгілі сипатта даярлап, кө птеген тә жірибелер жү ргізді. Олардың нә тижесі Лаплас заң ына қ айшы келмеді. Сонымен, ол ә ртү рлі биіктіктегі бө лшектердің санын анық тай келіп, Авогадро санының мә нін асқ ан дә лдікпен табуғ а болатынын кө рсетті.

Перрен ө з тә жірибелерінің нә тижесінде басқ а да ә дістер мен тең деулер кө мегімен анық талғ ан Авогадро санының мә нінен алшақ емес, қ анағ аттанарлық тай дерек алды. Олай болса Перрен ең бектеріндегі зерттеулер тек молекулалық -кинетикалық теорияның дұ рыстығ ын дә лелдеп қ ана қ оймай, оны коллоидтық -дисперстік системаларғ а да қ олдануғ а болатынын бұ лжытпай, ешбір шү бә сіз дә лелдеп берді.

Коллоидты системалардың реологиялық қ асиетіне системадағ ы дисперстік фазаның концентрациясымен қ атар, дисперстік орта мен дисперстік фаза табиғ аты секілді факторлар кү шті ә сер етеді. Олай болса, коллоидты системалардың реологиялық қ асиеттері осы жоғ арыда айтылғ ан себептерге байланысты туындайтындық тан, бір жағ ынан соларғ а, екіншіден ә лгі фактордың ө зіне ә сер ететін молеклалық ә рекеттесуді де қ арастырады.

Бағ ытталғ ан механикалық жү к дисперстік системадағ ы бө ліктердің жылжуын тудырады. Оның екі тү рі болуы мү мкін: жү к тұ рақ ты ә сер еткенде система нү ктелері жылжуын тоқ татады; системағ а сыртқ ы кү ш ә сер етіп тұ рғ ан кезде тұ рақ ты система бө лшектері ү немі қ озғ алыста болады. Бірінші жағ дайда бө лшектердің салыстырмалы жылжуы мен сыртқ ы механикалық кү штер арасындағ ы тә уелділік сипаты анық талады. Екінші жағ дайда ағ ымдылық деп аталатын сыртқ ы кү ш ә серінен бө лшектердің салыстырмалы жылжу жылдамдығ ының тә уелділігі анық талады. Деформация мен тұ рақ ты ағ ымдылық жылдамдығ ы арасындағ ы тепе-тең дік белгілі бір уақ ыт ө ткен соң орнайды. Система ө зінің соң ғ ы кү йіне келетін уақ ытты зерттеудің теориялық жә не қ олданбалық мә ні зор. Коллоидты системаның реологиялық қ асиетін зерттей отырып, олардың қ ұ рылымының пайда болу сипаты анық талады жә не мұ ның практикалық мә ні зор. Мысалы, жер қ ыртысы жә не оның қ ұ нарлығ ы, кірпіш ө ң дірісіндегі балшық қ асиеті, цемент ерітіндісі, тү рлі бояулар, лактар, пасталар, қ амыр, май сияқ тылардың бә рі де реологиялық жә не қ ұ рылымдық -механикалық қ асиетпен сипатталады.

Реологиялық қ исық тар жә не қ ұ рылымдау. Сұ йық заттардың тұ тқ ырлығ ын ө лшейтін аспап вискозиметр деп аталатыны физикадан белгілі. Коллоидты системалардың вискозиметрлік зерттеуін график арқ ылы кө рсетуге болады. Ә детте, мұ ндай графиктің екі тү рі бар: олардың біреуі ығ ысу кернеуі τ (немесе оғ ан пропорционал шама) мен жылдамдық градиенті Е (немесе оғ ан пропорционал шамалар), ал келесісі тұ тқ ырлық – ығ ысу кернеуі координатында тұ рғ ызылады. Ә детте, ығ ысу кернеуіне тура пропорционал шама ретінде капиллярлі вискозиметрдегі қ ысым тең деуі, ротационды вискозиметрдегі жіптің бұ ралу моменті, Хепплер вискозиметріндегі шариктің салмағ ы жә не басқ алар пайдаланылады. Ал, жылдамдық градиентіне тура пропорционал шама ретінде капиллярлі вискозиметрдегі цилиндрдің бұ рыштық жылдамдығ ы, Хепплер вискозиметріндегі шарик жылдамдығ ы алынады.

Жоғ арыда айтылғ ан координатқ а орай болатын реологилық қ исық тар кө руге болады. Олар су жә не бейорганикалық тұ здардың, қ ышқ ылдардың, негіздердің, глюкозаның, сахарозаның судағ ы ерітінділері жә не бензин, бензол, спирт сияқ ты сұ йық тарғ а тә н. Олардың тұ тқ ырлығ ы тү зу сызық тың котангенсті кө лбеулік бұ рышына тура пропорционал. Олардың тұ тқ ырлығ ы тұ рақ ты болғ андық тан, ол абцисса осіне паралелль тү зу сызық арқ ылы сипатталады. Жә не ондағ ы тү зу реті ерітінділердегі, сұ йық тағ ы тұ тқ ырлық тың артуына сә йкес орналасқ ан.

Мұ ндай сұ йық тарды ньютондық немесе идеал тұ тқ ыр деп атайды. Демек, тұ тқ ырлығ ы ығ ысу кернеуіне немесе жылдамдық градиентіне тә уелді системалардағ ы сұ йық тарды ньютондық дейді екен. Оғ ан жоғ ары молекулалық қ осылыстар ерітінділері жә не анизодиаметрлік бө лшектері бар дисперсті системалар жатады.

Тұ тқ ыр сұ йық тар вискозиметр арқ ылы ө ткенде жылу бө лінеді. Мұ ндай механикалық энергияның жылулық қ а тү рленуін вискозиметрлік ө лшеу кезінде ескерген жө н. Сұ йық тар ақ қ андағ ы энергетикалық шығ ындарды талдай білу дисперстік фазаның сұ йық тұ тқ ырлығ ына ық палын анық тауғ а кө мектеседі. Шар тә різді қ атты бө лшектерден қ ұ ралғ ан дисперстік фазасы бар коллоидты система ақ қ ан кезде ә лгі бө лшектердің ағ у жылдамдығ ы бұ рыштық жылдамдық тың жартысындай шамағ а тең болады. Мұ ндай жағ дайда энергия ілгерілмелі жә не айналмалы қ озғ алысқ а жұ мсалады. Ендеше, дисперстік фазаның кө лемі артқ ан сайын системаның тұ тқ ырлығ ы да артуы керек. Бұ л қ атынастың сандық сипатын анық тайтын тең деуді 1906 жылы А. Эйнштейн ұ сынды:

η = η ₀ (1 + 2, 5 φ ) (60)

мұ ндағ ы η – дисперстік система тұ тқ ырлығ ы; η ₀ – дисперстік ортаның тұ тқ ырлығ ы; φ – дисперстік фазаның кө лемі.

Жоғ арыдағ ы тең деуді Эйнштейн тең деуі дейді жә не ол анизодиаметрлік бө лшектері бар дисперстік фазаларғ а қ олдана бермейді. Мұ ндай бө лшектер ығ ысу жылдамдығ ы тө мендегенде сұ йық та ресіз (броундық қ озғ алыс) айналады. Ондағ ы бө лшектердің біразы ағ у жолында кө лденең тұ рып қ алуы мү мкін жә не мұ ның салдарынан дисперстік ортаның тұ тқ ырлығ ы артады. Жылдамдық жоғ арылағ анда, бө лшектер ағ ыс бағ ытына сә йкес орналасады да системаның тұ тқ ырлығ ы азаяды. Тұ тқ ырлық тың жылдамдық градиентіне мұ ндай тә уелділігі ньютондық емес сұ йық тарғ а тә н.

Дисперстік системаның тұ тқ ырлығ ына диспрстік фазадағ ы бө лшектердің ө зара ә рекеттесуі де ық палын тигізеді. Бұ л, ә сіресе ұ зын не созылғ ан бө лшектері бар системалар ү шін жоғ ары дә режелікпен сипатталады. Мұ ндай бө лшектердің беткі қ абатының кейбір жерінде адсорбциялық немесе сольваттық қ абаттар жоқ; молекулааралық ә рекеттесу салдарынан бө лшектер осы бос жерлер арқ ылы тү йісіп, жабысады. Олар толық жанасайын десе, оғ ан беткі қ абаттың қ алғ ан бө ліктерінде орналасқ ан қ орғ аушы қ абаттар кедергі болады. Осылайша, ө зінде қ озғ алмайтын (иммобилденген) сұ йығ ы бар агрегаттар пайда бола бастайды.

Система баяу жылдамдық пен ақ қ анда, бө лшектер арасындағ ы ажырап қ алғ ан іліністер қ айтадан жалғ асып, система тұ тқ ырлығ ы артады. Ал, керісінше, ағ ымның жоғ ары жылдамдық та болуы қ айтадан ілінісуге кедергі жасайды жә не ондағ ы қ ұ рылымдар бұ зылады да, бұ л тұ рақ танғ ан сұ йық кө лемін жә не тұ тқ ырлығ ын кемітеді. Мұ ндай системалар ү шін реологиялық қ исық тарда тұ тқ ырлық тың тұ рақ ты екібө лігі болады. Оның біріншісі ә лі бұ зылмағ ан, ал екіншісі толық бұ зылғ ан қ ұ рылымдарғ а сә йкес. Олардың арасында ауыспалы тұ тқ ырлық бө лігі орналасады жә не ол тү рлі дә режедегі қ ұ рылымның бұ зылуына орай келеді.

Системадағ ы бө лшектер ө зара ә рекеттескенде сұ йық кө лемін «кө ктеп ө тетін» ұ зын тізбек пайда болады. Ондағ ы туындайтын қ ұ рылым ү ш ө лшемді тор секілді. Бұ рын да ескергендей, тіпті кішкентай жылдамдық градиентіне сә йкес болатын шамалы ғ ана ығ ысу кернеуінде де бө лшектер бекітілген орнында-ақ бұ рылуғ а бейім, мұ ны басқ аша айтқ анда, тор тү йініндегі бө лшек бұ рылып, система ағ ымын қ амтамассыз етеді.

Қ ұ рылымның пайда болуын зерттеу тұ рақ тылық жә не дисперстік системаны тұ рақ тандыру мә селелерімен байланысты. Сонымен дисперстік системаларғ а жоғ ары молекулалық қ осылысты енгізу арқ ылы ү ш ө лшемді тор тү йінінде дисперстік фаза бө лшегі орналасатын қ ұ рылымды тудыруғ а болады. Бұ л тор системадағ ы агрегаттық тұ рақ тылық ты қ амтамассыз етіп, бө лшек қ озғ алысын шектейді. Олай болса, системадағ ы қ ұ рылымның пайда болуы, оның агрегаттық тұ рақ тылығ ын кемітеді.

Бө лшектердің концентрациясы ө скен сайын олардың арасындағ ы байланыстар да артады. 10-суретте дисперстік фазаның концентрациясына байланысты реологиялық қ исық тардың тә уелділігі кескінделген. Ал бө лшектер арасындағ ы байланыстар реологиялық қ исық тардың бастапқ ы кезінде ғ ана айтарлық тай ық пал етеді. Сол сияқ ты байланыс саны кө бейіп, ығ ысу кернеуі тө мендегенде системаның ағ ымы ә лсірейді. Тек жоғ арғ ы ығ ысу кернеуі кезінде ғ ана ағ ым жылдамдығ ы кө теріледі. Мұ ндай система ағ ымының едә уір жылдамдығ ы бар сә ттегі ең кіші ығ ысу кернеуін шекті ығ ысу кернеуі деп атайды. Шектіден аз ығ ысу кернеуі системада серпімді деформацияны тудырады. Мұ ндай жағ дайда системаның қ ұ рылымдануы ө зін қ атты денеше ұ стайды. Сондық тан да П. Ребиндер қ ұ рылымдық системаны сұ йық тә різді, ағ ымдық шегі бар системалар деуді ұ сынды.

⇐ Предыдущая 3 4 5 6 789 10 11 12 Следующая ⇒