2. Коллоидты жүйелердің молекулалы-кинетикалық қасиеттері

Броундық қ озғ алыс. 1827 жылы ағ ылшын ботанигі Р. Броун гү л тозаң дарының сулы суспензиясын микроскопта кө ре отырып, олардың ү здіксіз ретсіз қ озғ алыста болатындығ ын жә не ол қ озғ алыстың уақ ыт ө те келе тоқ тамайтындығ ын жә не сыртқ ы энергия кө здеріне тә уелді емес екендігін бақ ылағ ан. Коллоидты жә не микрогетерогенді жү йелердегі бө лшектердің жылулық қ озғ алысы броундық қ озғ алыс деп аталды.
Броун анық тай алмағ ан бұ л қ ұ былыстың табиғ атын кө птеген зерттеушілер кейіннен тозаң ның тіршілік ә рекетімен, жү йеде конвекциялық ағ ындардың болуымен, электрлік қ ұ былыстармен, ортаның бө лшектердің бетін ә р тү рлі шылауымен тү сіндіруге тырысты. Бірақ мұ ның бә рі дұ рыс болмады. Тек 1888 жылы Гуи жә не 1900 жылы Экснер броундық қ озғ алыстың молекулярлы – кинетикалық табиғ аты бар екендігі, яғ ни жылулық қ озғ алыс салдарынан болатындығ ы туралы ұ йғ арым жасады. Бұ л ұ йғ арымның дұ рыстығ ы Энштейн мен Смолуховскийдің теориялық есептеулерімен, Перрен, Сведбергтің эксперименттік жұ мыстарымен дә лелденді. Қ азіргі кезде коллоидты бө лшектердің бұ л қ озғ алысы жылулық қ озғ алыста болатын орта молекулаларының коллоидты бө лшектерді ретсіз соқ қ ылауы салдарынан туындайтыны анық талды.

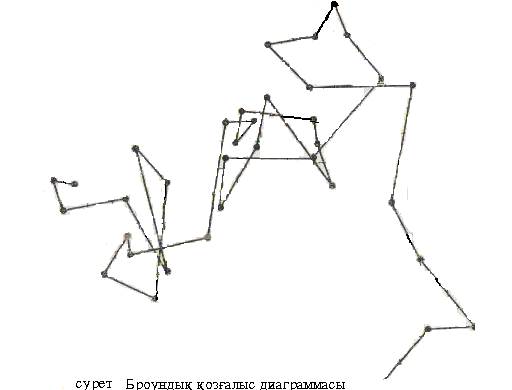
1-сурет. Броундық қ озғ алыс диаграммасы

Егер бө лшек ө лшемі айтарлық тай кішкентай болса, оғ ан жан-жағ ынан келетін соқ қ ылар саны бірдей емес болып, бө лшек ө те кұ рделі траектория бойынша ә р тү рлі бағ ытта қ озғ алады. Бө лшек ө лшемі мен массасы артқ ан сайын, соқ қ ылардың компенсациялану ық тималдығ ы да артып, бө лшек инерциясы да ү лкен болады. Осылайша, ө лшемі 5 мкм шамасындағ ы ү лкен бө лшектер белгілі-бір орталық маң айында толқ ындық (колебательные) қ озғ алыстарғ а ие болады. Ал бө лшек диаметрі 5 мкм жоғ ары болса, броундық қ озғ алыс тоқ тайды.

Орта молекулаларының ө те кө п соқ қ ылауы салдарынан коллоидты бө лшектер ө з бағ ыты мен жылдамдығ ын ө те жиі ө згертеді. 1секундта коллоидты бө лшек ө з бағ ытын 10²⁰ –нен артық ө згертуі мү мкін. Мұ ндай жағ дайларда коллоидты бө лшектің шын мә ніндегі жү рген жолын анық тау мү мкін емес, бірақ оның уақ ыт бірлігінде жү ріп ө ткен орташа қ ашық тығ ын анық тау оң ай. Ә детте бө лшектің белгілі бір бағ ыттағ ы қ озғ алысын білу қ ызығ ушылық тудыратындық тан (мысалы: диффузия жү ретін бағ ытта), онда сандық есептеулер ү шін ығ ысудың (смещение) ө зін емес, таң дап алынғ ан бағ ытқ а параллель х осіне бө лшектің ығ ысу проекциясының орташа квадраттық мә нін алады. Бө лшектің ығ ысу проекциясының орташа арифметикалық мә нін қ олдану мү мкін емес, себебі бө лшектің барлық бағ ыт бойынша қ озғ алу ық тималдылығ ы тең болғ андық тан, ол нө лге тең. Ығ ысу проекциясының орташа квадраттық мә ні мынадай тең деу арқ ылы табылады:

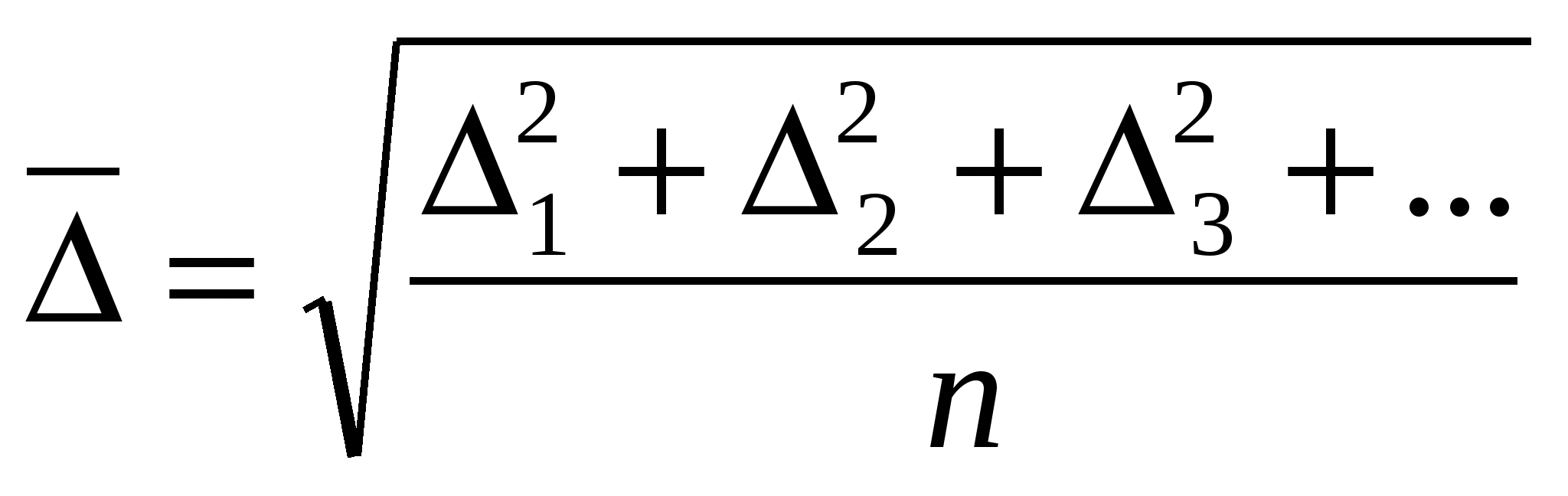
Мұ ндағ ы Δ ₁, Δ ₂, Δ ₃ – т. с. с. х осі бойынша бө лшектер ығ ысуының жеке проекциялары; n – есептеуге алынғ ан осындай проекциялар саны.
1888 жылы Гуи, 1900 жылы Экснер броундық қ озғ алыстың табиғ аты молекулалық -кинетикалық теорияғ а, яғ ни жылу ә серінен пайда болатын қ озғ алысқ а негізделуі мү мкін деген пікір айтты. Бұ л пікір Эйнштейн жә не Смолуховский есептеулері арқ ылы дә лелденіп, Перрен жә не Сведберг зерттеулеріндегі асқ ан дә лдікпен жү ргізілген тә жірибелер кезінде нақ тылы деректермен толық тырылды. Кө птеген тә жірибелер броундық қ озғ алыс зат табиғ атына тә уелсіз, ал бө лшектің ө лшеміне, ол орналасқ ан ортаның температурасы мен тұ тқ ырлығ ына тә уелді екенін кө рсетті. Еріткіш молекулаларының тынымсыз соқ қ ылауы салдарынан да дисперсті фазаның бө лшектері ретсіз қ озғ алысқ а тү седі. Ә рбір бө лшектің қ озғ алысы немесе белгілі мерзімдегі орын ауысып жылжуы қ ақ тығ ысудың орташа мә ні ретінде қ абылданды. Мысалы, бір бө лшек бір секундта шамамен 10²⁰ қ ақ тығ ысуғ а душар болады екен. Бө лшек ө те кішкене болса, оның жан-жағ ынан немесе ә р тұ сынан тиетін соқ қ ы саны бірдей бола бермейді жә не кең істіктегі мұ ндай бө лшек ө те кү рделі ізбен (траекториямен) жылжиды. Егер дисперсті фазадағ ы бө лшектің ө лшемі мен массасы белгілі бір шектен асып кететін болса, онда қ ақ тығ ысулардың бірін-бірі жою мү мкіндігі арта тү седі. Сондық тан да ө лшем 4-5 ммк болатын бө лшектер ө те жай тербелмелі қ озғ алыста болады. Ал бө лшек мұ нан ірі болса, броундық қ озғ алыс байқ алмайды.

Коллоидты системаны микроскоп арқ ылы бақ ылағ анда, ондағ ы белгілі бір бө лшекті х деп белгілеп, оның траекториясын анық тасақ, ол кө рсетілгендей болады да белгілі мерзімдегі орташа жылжуы ∆ х-ке тең еледі. Бұ л тү рлі бағ ыттағ ы кө птеген қ озғ алыстың статистикалық нә тижесі немесе кө лең ке іспеттес проекциясы. Ал броундық қ озғ алыстағ ы бө лшектің шын мә ніндегі траекториясын молекулалардікіндей дә л кө ріп бақ ылау мү мкін емес, ө йткені олар ө те кө п. Ондағ ы ә рбір бө лшек тек бір секундтың ө зінде есепсіз соқ тығ ысып, ө з бағ ытын есепсіз ө згертеді. Ал адам ө те ү лкейтілген бө лшектің бір секундтағ ы тек 10 шақ ты қ озғ алысын кө ре алады екен. Сондық тан броундық қ озғ алыс теориясына газ молекуласына қ олданылып келген орташа квадраттық жылжу деген ұ ғ ым енгізілді. Ол кө рсетілгендегідей бө лшектің t уақ ытта А мен В жағ дайғ а ө згеруі. Кейде оны орташа проекция деп те атайды. Бө лшектің орташа жылжуының (∆ х) уақ ыт пен диффузия коэффициентіне тә уелділігі Эйнштейн тең деуімен ө рнектеледі:

∆ х²= 2Dt; ∆ x = 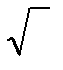2Dt(34)

мұ ндағ ы ∆ x – орташа жылжуы; ∆ х²– орташа квадраттық жылжу; t – жылжуғ а кеткен уақ ыт; D- диффузия коэффициенті. Дисперсті ортадағ ы молекуладан ү лкен ө лшемде болатын дисперсті шар тә різді бө лшектің диффузия коэффициентінің мә ні былай анық талады:

D = RT / NA•1 / 6π η r (35) Соң ғ ы екі тең деудің коллоидты химиядағ ы мә ні ерекше. Онда диффузия коэффициентін анық тау арқ ылы шар тә різді коллоидты бө лшектің радиусын есептеуге жә не сол сияқ ты жоғ арғ ы молекулалық қ осылыстардың шамасын ө лшеуге болады. Ал бө лшек кү рделі пішінді болса, соң ғ ы тең деудің оң жақ тағ ы соң ғ ы мү шесі (6π η r) біршама кү рделенеді. Ол ү шін (2) тең деудегі диффузия коэффициентінің мә нін оның алдың дағ ы (1) тең деуге қ ойып, бө лшектің орташа жылжуын есептейді:

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒