Тақырып 13. Кодалық ара-қашықтықтың кодтың түзету қабілетімен байланысы

⇐ ПредыдущаяСтр 31 из 40Следующая ⇒

Дә рістің мақ саты: Кодалық ара-қ ашық тық тү сінігін мең геру

Сұ рақ тар:

1. Максималды шынайылық тә сілі

2. Минималды кодалық ара қ ашық тық дегеніміз не?

3. Ара қ ашық тық матрицасы қ алай қ ұ рылады?

4. Жұ птық бақ ылауы неге негізделген?

Берілгеннен ең аз санғ а ерекшелейтін, тә уелсіз қ ателіктер кезінде қ одалық комбинацияғ а ауысу мү мкіндігі туады.

Екі кез-келген кодалық комбинацияның айырмашылық дә режесі Хэмминг мағ ынсында қ ашық тық пен сипатталады жә не кодалық ара-қ ашық тық деп аталады.

Кодалық ара-қ ашық тық комбинациялары бір-бірінен ерекшеленетін символ санымен сипатталады.

Екілік кодта екі комбинация арасындағ ы кодалық ара-қ ашық тық ты алу ү шін осы комбинациялардың суммасының 2 модулі бойынша бірліктердің санын табу жеткілікті.

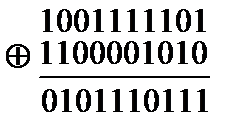
(2 модулі бойынша қ осу: y=x1+x2 қ осынды 1 ге тең болады егер x1мен x2 бір бірімен сә йкес келмесе )

Барлық кодалық рұ қ сат етілген комбинация жұ птары бойынша алынғ ан минималды қ ашық тық минималды кодалық қ ашық тық деп аталады.

Котдың қ асиетінің толық бейнесін D матрица қ ашық тығ ы береді.

23мысал: Симметриялық матрицамен код арақ ашық тығ ын қ ұ ру х₁= 000; х₂= 001; х₃= 010; х₄= 111.

Шешімі. 1. Код ү шін минимальды кодтыұ арақ ашық тық d=1

2. Код ү шін тө ртінші ретті симметриялық матрица

4. 1 таблица

	x1	x2	x3	x4

x1
x2
x3
x4

Қ абылдаудан кейін қ айта кодолау былайша жү ргізіледі, қ абылданғ ан код рұ қ сат етілген бойынша тең дестіріледі, яғ ни одан ең аз кодтық арақ ашық тық бойынша.

Мұ ндай қ айта кодолау максимальды ұ қ састық кодалауы деп аталады.

D=1 кодтық арақ ашық тығ ында барлық кодтық қ ұ рылымғ а рұ қ сат етілген.

Мысалы, n=3 рұ қ сат етілген қ ұ рылымында келесідей болады: 000, 001, 010, 011, 100, 101, 110, 111.

Кез келген бірлік қ ателік берілген қ ұ рылымнан басқ а рұ қ сат етілген қ ұ рылымғ а транспорленеді. Бұ л қ ателік тү зеуге қ абілетсіз жағ дайы.

Егер d = 2 онда бірлік қ ателіктегі рұ қ сат етілген қ ұ рылымнан басқ а рұ қ сат етілген қ ұ рылымғ а ө тпейді. Мысалы, кө п жағ дайда рұ қ сат етілген кодтық қ ұ рылым бірлік санның жұ птығ ы бойынша жасалуы мү мкін. Мысалы n=3 ү шін:

000, 011, 101, 110 – рұ қ сат етілген қ ұ рылым;

001, 010, 100, 111 – рұ қ сат етілмеген қ ұ рылым;

Код бірлік қ ателікті кө рсетеді, сондай-ақ тақ еселік қ ателіктерді кө рсетеді(n=3 ү шін).

Жалпы жағ дайда еселік қ ателікті кө рсетуде r дейін минимальды хэмминг арақ ашық тығ ы рұ қ сат етілген код қ ұ рылымында 1-ден артық болуы тиіс d_{0 min}³ r+1.

Шынында бұ л жағ дайда еселік ө спейді, яғ ни бір рұ қ сат етілген қ ұ рылымнан басқ асына ауысатын жағ дайда емес.

Бірлік қ ателікті жө ндеу ү шін кодтық қ ұ рылымды кө птеген рұ қ сат етілмеген кодтық қ ұ рылыммен салыстыру керек. ү шін

Кө птеген жағ дайда қ иып ө тпес ү шін хэмминг қ ашық тығ ы рұ қ сат етілген кодтық қ ұ рылым ү шін 3-тен кем болмауы тиіс. n=3 ү шін рұ қ сат етілген кодтық комбинацияда 000 жә не 111 қ абылдауғ а болады. Сонда рұ қ сат етілген қ ұ рылым 000 –ді кө птеген рұ қ сат етілмеген қ ұ рылымдардан яғ ни 000 қ ұ рылымында екілік қ ателікті қ орытады 001, 010, 100 бұ рын жазу керек.

Подобным же образом разрешенной комбинации 111 необходимо приписать подмножество запрещенных кодовых комбинаций: 110, 011, 101, образующихся в результате возникновения единичной ошибки в комбинации 111:

Сол сияқ ты 111 рұ қ сат етілген қ ұ рылымында мына рұ қ сат етілмеген код қ ұ рылымдарын бұ рын жазу керек 110, 011, 101, яғ ни 111 қ ұ рылымында қ орытындысында бірлік қ ателікті шығ арады.

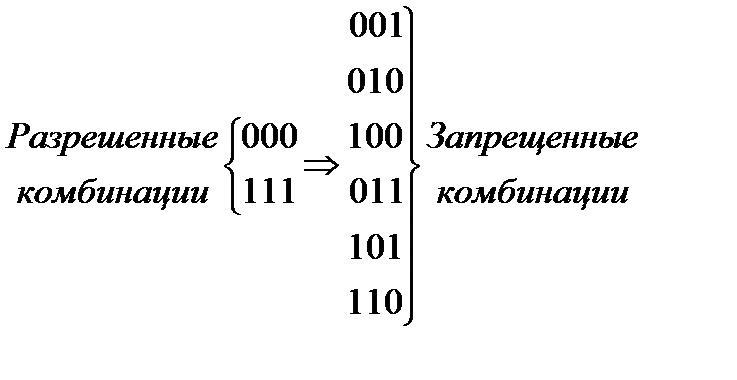
Жалпы жағ дайда бар мү мкіндігінше барлық қ ателікті табу ү шін s –ке дейін қ айта кодалауды қ оса алғ анда максимальды ұ қ састық, ә рбір қ ателік рұ қ сат етілмеген қ ұ рылымғ а ө туі тиіс.

Кез келген n – разрядты екілік қ ұ рылым m-ші бірлік куб, яғ ни қ ыры ұ зындығ ымен тү сіндірілуі мү мкін.

n=2 кодтық қ ұ рылымында квадрат тө бесінде орналасады.

d=2

Рис. 4. 2.

Жалпы жағ дайда n –ө лшемді кубта 2ⁿтө белері болады, кодтық қ ұ рылымның мү мкін болар жоғ ары мә ніне тең.

Мұ ндай модель қ арапайым геометриялық интерпретация жә не бө лек кодтық қ ұ рылымдағ ы кодтық қ ашық тық ты береді. Ол кубтың бірлік кбтың кіші қ абырғ аларының санына тең. Егер бұ зылғ ан қ ұ рылым алғ ашқ ысына ұ қ сас тү рде қ алса басқ а рұ қ сат етілген қ ұ рылымдарғ а қ арағ анда, онда қ ателік тек табылып қ ана қ оймас жө нделеді, яғ ни мынадай болу керек: немесе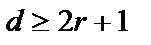

Жалпы, барлық қ ателік ұ стау ү шін жә не s еселікке дейін қ ателікті жө ндеу ү шін олдардық код арақ ашық тығ ы мынағ ан тең болу керек: d ³ r+s+1 (r³ s).

Бірлік тә уелсіз қ ателікті жө ндеудегі қ айта кодолау ә дісі келесідей тү сіндіріледі.

Кө п жағ дайда ә рбір рұ қ сат етілген қ ұ рылым ү шін барлық тө белері қ атысады, яғ ни (d-1)/2 радиусты жә не центрі тө беде. Егер қ орытындысында бө гет қ ұ рылымы сфера ішіндегі (d-1)/2 нү ктесіне ө тсе, онда ондай қ ателік жө нделеді.

Бақ ылау сұ рақ тары:

5. Максималды шынайылық тә сілі

6. Минималды кодалық ара қ ашық тық дегеніміз не?

7. Ара қ ашық тық матрицасы қ алай қ ұ рылады?

8. Жұ птық бақ ылауы неге негізделген?

⇐ Предыдущая 26 27 28 29 303132 33 34 35 Следующая ⇒