Тақырып №14 . Сызықты топтық кодтар. Туындау матрицасын құру

⇐ ПредыдущаяСтр 32 из 40Следующая ⇒

Тақ ырып №14. Сызық ты топтық кодтар. Туындау матрицасын қ ұ ру

Дә рістің мақ саты: Сызық ты топтық кодтар тү сінігін мең геру

Сұ рақ тар:

1. Желілік кодтар.

2. Желілік топтық кодтар қ алай қ ұ рылады?

3. Екілік желілік кодтар дегеніміз не?

4. Оларды қ алай қ ұ рады?

5. Жұ птық қ а тексеріс қ алай жү ргізіледі?

Сызық ты кодтар

Кодтар класының ішіндегі ең ү лкенін сызық ты кодтар қ ұ райды, олардың тексеру символдарының мә ндері анық талғ ан ақ параттық символдарғ а жасалғ ан операциялардың нә тижесінде анық талады. Екілік код жағ дайы ү шін ә рбір тексерілетін символ оның анық талғ ан ақ параттық символдардың суммасы 0-ге тең. Егер ақ параттық разрядтардың тексерілетін тең деуге кіретін бірлік саны тақ болса немесе 0-дер саны жұ п болса, тексерілетін позицияның мә ні 1-ге тең болады. Тең деулердің ә рқ айсысына кіретін тексерілетін тең деу саны жә не анық ақ параттық разрядтардың саны, берілген код қ андай жә не қ анша қ ателерді жө ндеп немесе табуына байланысты анық талады. Тексерілетін символдар кодтық комбинациялардың кез-келген жерінде орналасуы мү мкін. Декодтау кезінде тексерілетін тең деулердің ә ділдігі анық талады. Екілік код жағ дайында бұ л анық тау символдар арасындағ ы бірлік санының жұ птық қ а тексерілуіне негізделеді. Тексерістердің жиынтығ ы қ ай позицияларда символдар бұ рмалатыны туралы ақ парат алуғ а мү мкіндік береді.

Кез-келген екілік код топтық код болып табылады, себебі оғ ан енетін код комбинацияларының жиынтығ ы топты қ ұ райды. Сызық ты жә не топтық кодтар тү сінігін анық тау сызық ты алгебраның негізімен танысуды талап етеді.

Сызық ты кодтарғ а математикалық кіріспе

Сызық ты кодтарды математикалық бейнелеудің негізі сызық ты алгебра болып табылады (векторлық кең істік теориясы, матрицалар теориясы, топтар теориясы). Кодтық комбинацияларды кө бейткіштер элементтері ретінде қ арастырады, мысалы, екілік кодтың кодалық комбинациялары екілік оң дық сандар кө бейткіштеріне жатады.

Кейбір алгебралық операциялары анық талғ ан кө бейткіштерді алгебралық жү йелер деп атайды. Алгебралық жү йе деп анық талғ ан ережелермен екі элементті ү шінші элементпен салыстыру. Ә детте негізгі операцияны қ осу деп атайды (a+b=c кө рсетіледі) немесе кө бейту (a*b=c кө рсетіледі), ал оғ ан қ арсы – алу немесе бө лу, тіпті, егер осы операциялар сандармен орындалмаса жә не сә йкес арифметикалық операцияларғ а ұ қ самайтын болса да.

Тү зейтін кодтар теориясында кө п пайдаланылатын негізгі алгебралық жү йелер теориясын кысқ аша қ арастырамыз.

Элементтер жиынтық тобында Бір негізгі операция анық талғ ан жә не келесі аксиомалар орындалады:

1. Операцияларды топтың кез-келген екі элементіне қ олданса, онда сол топтың элементі пайда болады (тұ йық тар талабы).

2. a, b, c тобының кез-келген ү ш элементін мына тең дік қ анағ аттандырады (a+b)+c=a+(b+c), егер негізгі операция – қ осу, жә не a(bc)=(ab)c тең дігі, егер негізге операция - кө бейту.

3. Кез-келген G_nтобында G_n барлық а мә ндерінде а+0=0+а шартын, егер негізгі операция – қ осу, немесе а*1=1*а=а шартын, егер негізгі операция – кө бейтуді қ анағ аттандыратын анық талғ ан элемент болады. Бірінші жағ дайда ол элементті нө л деп атайды жә не 0 символымен белгілейді, ал екінші жағ дайда – бірлік жә не 1 символымен белгілейді.

4. а тобындағ ы кез-келген элемент а+(-а)=-а+а=0 тең дігімен анық талғ ан, егер негізгі операция – қ осу, егер негізгі операция – кө бейту, онда а*а^-1= а^-1*а=1 тең дігімен анық талатын элементі болады.

Бірінші жағ дайда ол элементті қ арама-қ арсы деп атайды жә не (-а) белгілейді, ал екінші жағ дайда – кері жә не а^-1белгілейді.

Егер топта анық талғ ан операция коммутативтік болса, онда a+b=b+a тең дігі дұ рыс (қ осу тобына) немесе a*b=b*a тең дігі (кө бейту тобына), онда топты коммутативтік деп атаймыз.

Соң ғ ы элементтер санынан тұ ратын топты топтың реті деп атайды.

Бізбен каралатын кө п n-разрядты кодалық комбинациялар соң ғ ы топ болуы ү шін, негізгі операцияны орындау кезінде нә тижелік кодалық комбинациялардағ ы разрядтар саны артпауы қ ажет. Бұ л шартты берілген модуль бойынша q (q – жә й сан) символдық разрядасты қ осу операциясы қ анағ аттандырғ андық тан, топ элементтерінің бірдей разрядты сандары жә й тү рде қ осылады, ал қ осындының нә тижесі болып алынғ ан санның q модуль бойынша бө лгендегі қ алдық саналады.

Екілік кодтарды қ арастырғ ан кезде модуль 2 бойынша қ осу операциясы қ олданылады. Егер ондағ ы бір сандарының қ осындысы жұ п болса берілген разряд цифрларының қ осындысының нә тижесі болып 0 табылады, егер 1 болса, онда бір сандарының қ осындысы тақ, мысалы,

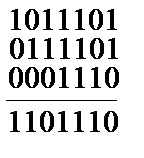
Бізбен таң далғ ан операция коммутативті, сондық тан қ аралатын топтар абелевті болады.

Нө лдерден тек тұ ратын комбинация нө лдік болады. 2 модуль бойынша қ осынды кезінде берілген элемент ө зі қ арама-қ арсы элемент болады. Демек, 2 модуль бойынша алу операциясы қ осу операциясына парапар.

24 мысал. Келесі берілген кодалық комбинациялар топтар ма екендігін анық тау:

1) 0001, 0110, 0111, 0011;

2) 0000, 1101, 1110, 0111;

3) 000, 001, 010, 011, 100, 101, 110, 111.

Шешімі: Бірінші кө пмү ше топ емес, себебі нө лдік элементі жоқ.

Екінші кө пмү ше де топ емес, себебі тұ йыталу шарты орындалмай тұ р, мысалы, 2 модул бойынша 1101 мен 1110 комбинацияларының соммасы алғ ашқ ы кө пмү шеге жатпайтын 0011 комбинациясын береді.

Ү шінші кө пмү ше барлық шарттарды қ анағ аттандырады жә не топ болып табылады.

Кө пмү шеасты топтар, операцияғ а қ атысты ө здері топ болып табылатын, топта анық талғ андарды – тобастылар деп атайды. Мысалы, ү шразрядты кодалық комбинациялар: 000, 001, 010, 011 кө рсетілген ү шразрядты кодалық комбинациялар тобы мысалында тобасты қ ұ райды.

G_n тобында белгілі бір А тобы берілсін. Егер В- А элементіндегі G_n –ғ а жатпайтын, онда В элементінің суммасы G_nтобындағ ы А тобын қ ұ рсын.

Кез келген топ нолдік элементті қ ұ райтындай, кө ршілес кластар В элемеентінен тұ рады. Қ ұ рылғ ан кө ршілес класқ а кірмейтін дә йекті тү рде В элементін алып, барлық топты А тобына ажыратуғ а болады.

B_jэлементі деп топ бойынша кө ршілес класты қ ұ райтын элементтерді атайды.

Топтық таблица деп аталатын ажырату таблицасында, қ ұ ратын элементтер бағ анның сол жағ ында орналасады, топтағ ы сол жақ элемент нолдік элемент болып табылады.

25 мысал: Ү ш разрядты екілік кодты комбинацияны, екі разрядты кодты комбинациялы топқ а ажырату.

Шешімі: Ажырату таблицағ а сай орындалады:

Таблица 4. 4.

A₁=0	A₂	A₃	A₄

B₁	A₂Å B₁	A₃Å B₁	A₄Å B₁

26 мысал: Тө рт разрядты екілік кодты комбинацияны, екі разрядты кодты комбинациялы топқ а ажырату.

Шешеімі: Кө птеген ажырату нұ сқ алары, кө ршілес кластардан тұ ратын элементтерді қ ұ райтынына тә уелді

Нұ сқ алардың бірі:

Таблица 4. 5.

A₁=0	A₂	A₃	A₄

B₁	A₂Å B₁	A₃Å B₁	A₄Å B₁
B₂	A₂Å B₂	A₃Å B₂	A₄Å B₂
B₃	A₂Å B₃	A₃Å B₃	A₄Å B₃

Сақ ина дегеніміз R-дің кө п элементтері, онда екі операция анық талғ ан (қ осу жә не кө бейту)олар:

1)қ атынас бойынша R элементінің топтық коммутациясы;

2)элементтер туындысы аÎ R жә не bÎ R, сосын R элементі бар(қ атынас жә не кө бейту бойынша тұ йық талуы);

3) R-ғ ы кез келген а, b, c ү ш элементі ү шін мына тең дік дұ рыс болады a(bc)=(ab)c (кө бейту ү шін ассоциациялық заң );

4) R-ғ ы кез келген а, b, c ү ш элементі ү шін мына қ атынас дұ рыс боладыa(b+c)=ab+ac и (b+c)a=ba+ca (дистрибутивті заң );

Егерде кез келген екі сақ ина ү шін мына тең дік дұ рыс болса, онда ол коммутативті деп аталады.

Сақ инада кө бейту жә не кері элементтер ү шін бірлік элемент болмау мү мкін.

Мысалы, сақ ина қ осу жә не кө бейту операцияларында кө птеген оң бү тін сандарғ а қ ызмет кө рсету мү мкін.

F аймағ ы дегеніміз-кө птеген, соның ішінде екі элемент арасында екі операция-қ осу жә не кө бейту, жә не келесі аксиомалар орындалады:

1)қ осу бойынша кө птеген элементтер коммутациялық топ қ ұ рады;

2)кө бейту бойынша кө птеген нө л емес элементтер коммутациялық топ қ ұ рады;

3)кез келген ү ш a, b, c элементі ү шін келесі қ атынас орындалады (b+c)=ab+ac (дистрибутивті заң ).

1) F аймағ ы, сә йкесінше, ә рбір нольдік емес элементте кері элементі бар болып келетін, кө бейту бойынша бірлік элементі бар коммутативті сақ ина болып табылады, Мысал аймағ ына кө птеген оң сандарды жатқ ызумызғ а болады.

2) GF(P) аймағ ы P элементтерден тұ ратын соң ғ ы сандарды соң ғ ы аймақ немесе Галуа аймағ ы деп аталады. Р сандарының ә рқ айсысына жай сандардың дең гейі болып келетін q аймағ ы бар, ол р элементтерін санайды.

3) Аймақ та екі элементтен кем емес болуы керек, Поле не может содержать менее двух элементов, ең болмағ анда оның қ ұ рамында қ осу операциясына(0) қ атысты бірлік элемент жә не алу операциясына қ атысты бірлік элемент болуы керек(1).. 0 жә не 1 қ амтитын аймақ ты GF(2) деп белгілейміз. Екі элемент аймағ ында орындалатын қ осу жә не алу ережелері мынадай:

+				×

5) 4. 5 сурет Екі элемент аймағ ында орындалатын қ осу жә не алу ережесі

7) Екілік кодтау комбинациясы GF(2), аймағ ындағ ы n элементтердің біркелкілік дә йектілігі болып табылады, олар жеке оқ иғ ағ а байланысты GF(P) аймағ ындаn элементтердің кодтай теориясында қ арастыралыды. Жай сандарды бірдей дең гейде ұ стап, Мұ ндай тә сіл кодтарды негізге ала отырып қ ұ руғ а жә не сараптауғ а болады. Жалпы жағ дайда A_jжә не A_iкодтық комбинациясының қ осындысын A_f= A_i+ A_j деп атайды, A_k(k=1, 2, …, n) символының қ осындысы k-х символдар комбинацисын ұ сынады. жә не де қ осындыны іске асыру GF(P) аймағ ынын ережесімен орындалады.

8) Жеке жағ дайда, код негізгісі q жай сан болып келсе, GF(q) аймағ ындағ ы қ осу ережесі q модуліне сә йкес келетін қ осу ережесімен тұ спа-тұ с келеді

Сызық тық векторлық кең істіктегі сызық тық код

Кө рсетілген алгебралық жү йелерге (топ, шар, ө ріс) операциялар математикалық объектілердің бір класына жатты. Мұ ндай операцияларды элементтер композициясының ішкі заң дары деп атайды.

Кодалау теориясында математикалық объектілердің (мысалы, L жә не W) екі класын біріктіретін модельдер кең інен қ олданылады. Композицияның ішкі заң дарында элементтер композициясының сыртқ ы заң дары ең гізіледі, wÎ W жә не аÎ L бойынша сÎ L болуы керек.

F элементі ө рісіндегі сызық тық векторлық кең істік деп (скалярлі) кө птеген элементтерді айтады V (векторлар), егер келесі аксиомалар орындалса:

1) кө птеген V бірігу операциялары жө ніндегі коммутативті топ болып саналады;

2) кез-келген вектор ү шін v -V-дан жә не кез-келген с -F-тан V –да тіркелген cv кө бейтіндісі болып табылады;

3) егер u жә не v -V векторынан, ал с жә не d -F скалярынан, онда

с(с+v)=cu+cv; (c+d)v=cv+dv (дистрибутивті заң дар);

4) егер v-вектор, ал с жә не d-скалярлар, онда (cd)v=c(dv) жә не 1*v=v

(скалярлар ү щін кө бейтілген ассоциативті заң ).

Жоғ арыда кө рсетілген кодалық комбинациялардың разрядты кө бейту ережелері анық талғ ан болатын. Енді n тізбегінен GF(P) ө рісіндегі элементтің a_i GF(P) тұ ратын кө бейтіндінің операциясын анық таймыз, ол келесідей кө бейтіледі: a_i(a₁, a₂, …, a_n)= (a_ia₁, a_ia₂, …, a_ia_n)

(элементтер кө бейтіндісі GF(P) ө рісінің ережелері бойынша анық талады).

Берілген операциялар бойынша дистрибутивті заң дар жә не ассоциативті заң дар (п. п. 3. 4) орындалады, n-разрядті кодалық комбинациялардағ ы барлық біріктірулерді GF(2)ө рісіндегі векторлық сызық тық кең істік деп қ арастыруымызғ а болады (т. е. 0 и 1). Біріктірулер разряд бойынша 2 модуль арқ ылы ө рнектеледі. Векторларды ө рістегі (1) бір элементке кө бейту барысында, ол ө згермейді, ал басқ асына кө бейту (0) 0=(0 0…0) символымен аталатын векторлық кең істіктегі бірлік элементке айналдырылады.

Егер сызық ты кең істікте n элементтің қ айталануынан GF(P) алаң ы анық талғ ан шартты қ анағ аттандыратын(қ ауымдастық, тұ йық талғ ан бейсызық тының скаляр кобейтіндіге қ атынасы)векторлық кө бейтіндінің қ осыша операциясын береді, онда n-разрядты кодалық комбинацияның барлық қ осындысы GF(P) коэффициентінің алаң ындағ ы сызық ты коммутативтік алгебрағ а айналады.

Векторлық кең істіктегі аксиоманы қ анағ аттандыратын векторлық кең істіктегі кө птеген элементтер кең істікішілік деп аталады.

GF(P) алаң ындағ ы барлық n-разрядты кодалық комбинациялар векторлық кең істіктегі кең істікішілік тудырушы кө птеген векторлар сызық тық кода деп аталады.

Екілік кодалық жағ дайда мұ ндай кең істікішілік комбинациялар GF(2) алаң ында барлық n-разрядты екілік кодалық комбинациялар топтарының топішілігі болып табылатын екілік кодалық комбинацияның кез келген қ осындысын тудырады.

Екілік топтық коданы қ ұ растыру

Таза тү зетілген коданы қ ұ растыру талап етілген Q кода кө лемінен асатын, яғ ни берілетін сандардың керекті командасы немесе ө лшенетін шаманың дискретті мә ні жә не байланыс арналарында қ олданылатын мү мкін векторлық қ ателіктің статикалық басқ аруды туғ ызады.

Векторлық қ ателік деп разряд бірліктеріне ие болатын, қ ателікке ә келетін n-разрядты екілік қ айталануды айтамыз. Кез келген қ ате кодалық комбинацияны енді қ осынды( немесе айырма) деп қ арастыруғ а болады.

2^к-1≥ Q тең сіздігінен шығ а отырып(0-дік комбинация байланыс арнасы кү йін ө згертпейтіндіктен жиі қ олданылмайды) қ арапайым екілік кодалық команданың берілісіне қ ажетті берілген сан, яғ ни к ақ параттық разрядты санын анық таймыз.

k –разрядты қ алдық сыз кодтың ә р 2^k - 1 нө лдік емес комбинациялары ү шін сә йкес п символдар комбинациясын қ ою керек. Тү ртіндінің мағ ыналарының ара п - k мынадай ә рекеттің тексерістің дә режелерінің арада нә тижеде жинақ та- ша 2 мағ ынаның модулю тү ртінді тағ айынды ақ параттық дә режелерде бекиді.

Ақ параттық тү ртіндінің (нө лдік емес қ оса) 2k ә рекетінің кө пшілігін дә режелі ә рекеттің барлық n- тобының топшасын тә рбиелейді, сол жә не кө рсетілген ережеге алғ ан дә режелі ә рекеттің 2k n- кө пшілігі де дә режелі кодтық ә рекеттің n- топ топша болып табылады. Рұ қ сат етідген кодтық ә рекеттің сол кө пшілігі топтық код болады.

Бізге тексерістің дә режесінің жә не абатшылық тардан тү ртіндінің ұ йғ арымі ү шін тексерістің дә режелерінде бас-басығ а деген кіріс ақ параттық дә реженің нө мірінің санын анық тау қ ажет.

2n топты дә режелі ә рекеттің барлық n- шектес сыныптарғ а 2k рұ қ сат етілген топшағ а дә режелі n- разрядты кодтық ә рекеттің тексеріс дә режелері мұ нда тағ ы толтырылмағ ан. Басқ а кода ө зінің топшасының бө лінуінде 2n - k - 1 шектес сыныптар саналады. Бас-басы сыныптың элементтері ө здігінен сомаларды кода жә не айтылмыш сыныптың тә рбиеле- элементінің 2 ә рекетінің модулю ұ сынады. Егер бас-басы сыныптың қ ұ рушы элементтерін қ абылдау ү шін тапсырынды арна ү шін қ атенің векторын, нешінші жө ндеулі болуғ а керек ең ық тимал байланыстарын, сол ара бас-басы шектес сыныпта, арада нә тижеде ә сердің тағ айынды векторғ а барлық адал ә рекеттеріне қ ате кодты ә рекет топталады. Кодты ә рекеттің кө рінген байланысын тү зетуі ү шін арнаның шығ а берісінде енді анық тау баршылық, қ анаттастық тың қ андай сыныбына ол қ арайды. Оны кейін(модуль 2 б/а) осы шектес сыныптың қ ұ рушы элементімен қ аттап сала, кода ақ иқ аттық ә рекетін аламыз.

Ортақ саннан 2n - 1 ық тимал қ ателердің топты код небә рі 2n - k - 1 қ атенің айырмашылығ ы б/а шектес сыныптың санына жө ндеу білетіні анық.

Қ андай шектес сыныпқ а алынғ ан ә рекет қ арайтынын туралы ақ паратты алу мү мкіндігі болу ү шің ә р шектес сыныпқ а сә йкес бір символдар бақ ылау тізбегі опознаватель(синдром) деп аталатын қ ойылу керек.

Егер тек қ ана барлық бірлік қ ателіктер емес, сонымен қ атар, екілік тә уелсіз қ ателіктерді ө ң деу керек болса, онда тең сіздіктің тү рі мынадай болады:

2^n-k-l +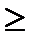

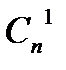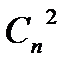
Жалпы жағ дайда барлық тә уелсіз қ ателіктерді s дә режесіне дейін ө ң деп қ оысмша тең сіздік аламыз:

2^n-k-l + +…+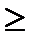

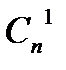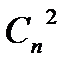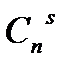
Айта кету керек, барлық жағ дайда практика жү зінде орындалмайтын жоғ арыда келтірілген қ атынастарда тексерілетін символдардың теориялық минималды мү мкін болатын сандар шегі кқ рсетілген. Сә йкес келетін тең деулерге қ арағ анда жиі тексерілетін символдарды кө п қ ажет етеді.

Ә рбір бастауыш қ ателікті ө ң деудің анық таушысын салыстыру процесін қ арастырғ анда бір себебі анық талады.

Бақ ылау сұ рақ тары:

1. Желілік кодтар.

2. Желілік топтық кодтар қ алай қ ұ рылады?

3. Екілік желілік кодтар дегеніміз не?

4. Оларды қ алай қ ұ рады?

5. Жұ птық қ а тексеріс қ алай жү ргізіледі?

⇐ Предыдущая 27 28 29 30 313233 34 35 36 Следующая ⇒