3-СҰРАҚ– 20 % Ұзын таңбалар тізбегін кодтаудың абзалдығын түсіндірңіз

3-СҰ РАҚ – 20 % Ұ зын таң балар тізбегін кодтаудың абзалдығ ын тү сіндірң із

БЧХ кодтары қ алағ анша ұ зындық ты жә не жылдамдық ты кодтардың ү лкен класын қ ұ рады.

Ұ зын таң балар тізбегін кодтаудың абзалдығ ы олардың параметрлерін оң ай жә не иілгіш тү рде екендігінде ғ ана емес, сонымен бірге, жиынтық тың ұ зындығ ы бірнеше жү зеге жеткенде, сол параметрлердегі ( жылдамдық пен ұ зындық ) кодтардың арасында олардың кө пшілігі тиімді болады. b ұ зындық ты қ ателер жиынтығ ын шеткі разрядтардың арасындағ ы бө геттермен бұ зылғ ан b-2 разряды бар бө гет комбинациясының тү рін тү сінеді. Мысалы, b=5 кезінде бө геттер комбинациясы, яғ ни қ ателер жиыны келесі тү рде болуы мү мкін: 10001 (тек шеткі екі символдар ғ ана бұ зылғ ан), 11111 (барлық символдар бұ зылғ ан ), 10111, 11101, 11011 (тек бір ғ ана символ бұ зылмағ ан), 10011, 11001, 10101 (ү ш символ бұ зылғ ан). Файра кодтары b ұ зындық ты қ ателер жиынын тү зете алады жә не b ұ зындық ты қ ателер жиынын таба алады.

4-СҰ РАҚ Есеп: - 40 %

200 детальдің ішінде 4 жарамсыз болу ық тималдығ ын табу керек. 1 элементтің жарамсыз болу ық тималдығ ы 0, 01 тең. P_n (k)=? P₂₀₀ (4)=?

Шешімі: n ө те ү лкен, ал p нің мә ні ө те кіші; сондық тан Пуассон тең деуін қ олданамыз: λ = 200 ● 0, 01=2;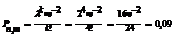

№2


C	C	C	A	E	C	B	A	A	D

1-сұ рақ 1. Ақ парат- бұ л беретін, сақ тайтын жә не ө ң дейтін жаң а мағ лұ мат.

Берілгендер- бұ л ЭЕМ ө ң дейтін сандық ақ парат.

Берілгендерді беру жү йесі ә р-тү рлі ақ параттық жү йені (АЖ) қ ұ руғ а қ ажет, мысалы: Таратушы есептеу жү йе режимінде жұ мыс істейтін АЖ. ЭЕМ желісі ұ йымдар пайдалана алатын ә р-тү рлі машина санынан тұ рады. Есептеу желісі кафедра, институт, қ ала, мемлекет жә не дү ние жү зі кө лемінде болуы мү мкін. Бұ л жағ дайда локальды есептеу жү йе шегіндегі ЭЕМ араларындағ ы сияқ ты берілгендерді беру жү йесінен тұ рады.

АҚ ПАРАТТАРДЫ БЕРУ ЖҮ ЙЕСІ. Ақ паратты берудің бір каналды жү йесінің қ ұ рылымдық сұ лбасы 3. 2. 1. 4. 1 суретте кө рсетілген. Ақ парат жү йеге хабарлама тү рінде келіп тү седі. Хабарлама деп, ақ параттан тұ ратын біріншілік сигналдар немесе таң балар жиынтығ ын айтады. Хабарлама кө зі жалпы жағ дайда ақ параттың кө з жиынтығ ын (зерттелетін немесе бақ ыланылатын нысанның ) жә не оның жағ дайы жө ніндегі немесе ө тіп жатқ ан процесс жө нінде ақ паратты қ абылдайтын бірінші ретті тү рлендіргішті (датчик, адам-оператор) қ ұ райды. Хабарлама дискретті жә не ү зіліссіз болып екіге бө лінеді. Дискретті хабарлама жекелеген элементтер мен таң баларды кө зін тізбектей жіберу нә тижесінде қ алыптасады. Кө птеген ә р-тү рлі таң баларды хабарлама кө зінің алфавиті деп атайды. Толығ ырақ айтсақ, ө зара байланысты ережени қ анағ аттандыратын табиғ и немесе жасанды тілдегі ә ріптер таң балар бола алады. Дискретті хабарламаның кең тарағ ан тү рі берілгендер болып табылады. Ү зіліссіз хабарламалар элементтерге бө лінбейді. Олар кө птеген шамаларды ү зіліссіз қ абылдйтын уақ ыт функциясымен тү сіндіріледі. Оғ ан мысал ретінде теледидар бейнесін, сө йлеуді алуғ а болады. Байланыс жү йесінде ү зіліссіз хабарламаларды беру сапасын жақ сарту ү шін дискреттіге тү рлендіреді. Байланыс каналы бойынша хабарламаны беру ү шін оғ ан белгілі бір сигналды сә йкес қ ою қ ажет. Ақ параттық жү йеде сигнал деп хабарламаны бейнелейтін (тасымалдайтын) физикалық процесті айтады. Хабарламаны сигналғ а тү рлендіру берілген байланыс каналы бойынша беруге ың ғ айлы, яғ ни кең мағ ынада кодттау деп атайды. Қ абылданғ ан сигнал бойынша хабарламаны қ алпына келтіру операциясы декодттау деп аталады. Ү лгілік сигналдардың қ арапайымдылығ ы мен айырып танудың (распознавания) біліктілігін қ амтамасыз ету ү шін олардың санын минимумғ а дейін қ ысқ арту қ ажет. Сондық тан, ереже бойынша бастапқ ы таң баларды басқ а символдар деп аталатын, аз таң ба мө лшеріндегі алфавитке келтіру керек. Бұ л операцияны белгілеу кезінде, тар мағ ынада қ арастырылатын, кодттау термині паидаланылады. Мұ ндай операцияны орындайтын қ ұ рылғ ы кодттаушы немесе кодер деп аталады. Символдар алфавиті таң балар алфавитінен аз болғ андық тан ә р таң бағ а, кодттық комбинация деп атайтын символдардың кейбір тізбегі сә йкес келеді. Кодттық комбинациядағ ы символдар саны оның маң ыздысы (значностью) ал, ноль емес символдар саны – салмақ деп аталады.

2-CҰ РАҚ – 20% Қ андай кодтардын кедергіге шыдамды деп атайды? Хэмминг коды - кедергіге қ алыпты қ арсы тұ ратын код. Шулы дискретті арнаның басты теоремасы бойынша, ақ парат жасаудың жылдамдығ ы арнаның ө ткізу қ абілетіне тең немесе одан кем болса, онда ақ параттық арна бойынша аз қ ателікпен жіберуге мү мкіндік беретін коды болады. Хэмминг коды хабарлауды максималды жылдамдық пен жә не минималды қ ателікпен кодалау мә селесін шешеді, яғ ни кедергіге тө зімді кодтау мә селесін шешеді. Бұ л мә селені шешудің арнайы ә дістері бар. Кең қ олданысқ а ие: алгебралық ә діс, оның кө мегімен топтық кодтар класы зерттелді, жә не геометриялық кодтар.

Кодтық аяның қ ұ рылысын біркелкі кодағ а қ олданып қ араймыз, дербес жағ дайда блоктық, кодтық комбинациялар бір біріне тә уелсіз кодтады жә не декодталады. Шығ у алфавиті В біркелкі n-ретті коды, Г m символдан қ ұ ралады; mсаны кодтын негізі деп аталады. Осындай кодтың кодалық комбинациясының тү рі мынадай ai a2... an, мұ нда ai мағ ынасы i-ші разрядты коды, i = 1, 2, ... , n, ai ϵ B алфавит символын реттейміз жә не m модулі бойынша есептеудің ә ртү рлі символды классы екенін тү сінеміз. Индекс классын m санын қ алдық ө кіліне бө лгенде қ оямыз.

3-СҰ РАҚ – 20% Неліктен кедергіге шыдамды кодтар қ ателіктерді анық тайды жә не тү зетеді?

Хэмминг коды - кедергіге қ алыпты қ арсы тұ ратын кодтар тек қ ана қ ателерды анық тауды ғ ана жү зеге асырмай сонымен қ атар оларды тү зетеді. Qm нан аспайтын еселіктердың қ ателеіктерін тү зетудің жалпы идеясы келесіде. М кедергіге қ алыпты қ арсы тұ ратын қ одтардың мү мкін болатын кодалық комбинациялары N класына бө лінеді. Бұ л бө ліну ә р классқ а бір рұ қ сат етілген жә не оғ ан жақ ын рұ қ сат етілмеген кодалық комбинация кіру керек. Қ айта кодтау кезінде қ абылданғ ан кодтық комбинация кай классқ а жататынын анық талады. Егер де кодтық комбинаия қ атеиен қ абылданса, яғ ни рұ қ сат етілмеген, онда ол ол классқ а жататын рұ қ сат етілгенге ө ң деледі. Кодтау теориясында Qm нан аспайтын еселіктердың қ ателеіктерін тү зету мү мкіндіктерін жү зеге асыру ү шін кодтық ара-қ ашық тық 2qm нан кө п болу керек екені дә лелденген. Кө біне ол d=2qn+1 формуласымен анық талады. n разрядты екілік кодты N кодтық комбинациясының ең ү лкен санын d қ ашық тық пен табу ерекше болып саналады.

4-СҰ РАҚ Есеп: - 40 %

Қ ұ рылғ ы 2000 элементтен қ ұ рылғ ан. Т уақ ытта элементтің істен шығ у ық тималдығ ы 0, 001 тең. Т уақ ытта 4 элементтің істен шығ у ық тималдығ ын табың ыз?

Шешімі: n ө те ү лкен, ал p нің мә ні ө те кіші; сондық тан Пуассон тең деуін қ олданамыз: λ = 200 ● 0, 01=2;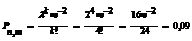

№3


A	E	D	E	A	C	D	B	D	B

1-сұ рақ 1. Сигнал кең істікпен уақ ытта ақ паратты тасу қ ұ ралы. Сигналдың материалдың негізін ақ парат тасығ ыш деп аталатын қ андай да бір физикалық объект немесе ү рдіс болып табылады. Тасығ ыш модуляция кезінде сигнал бола алады. Сигналдар моделдері Ақ парат тасығ ыш ретінде табиғ аттағ ы тү рлі тербеліс болады кө бінесе ол гармоникалық, тұ рақ ты жағ дай. Тербелістер детерминерленген жә не кездейсоқ болып бө лінеді. Жоғ арыда атап кө рсетілгендей, «сигнал» ұ ғ ымы кең мағ ынанны береді, яғ ни ол ақ паратты материалды тасығ ыш. Сигналдарғ а табиғ и сигналдар жә не арнайы бір мақ сат ү шін жасалғ ан сигналдар болып бө лінеді. Табиғ и сигналдарғ а жарық тық сигналдар, космостық сигналдар жатады. Арнай мақ сат ү шін жасалғ ан сигналдарғ а ү рдістегі немесе нысандағ ы ө згеріс жө ніндегі ақ паратты алу мақ сатында қ ұ рылғ ан сигналдар (эталлонды сигналдар). Сигнал ақ параттық жү йеде хабарламаны беруге арналғ ан арнайы қ ұ рылғ ы. Сигналдың материалды негізін, ақ паратты (хабарламаны) тасығ ыш деп аталатын физикалық нысан немесе ү рдіс қ ұ райды. Тасығ ыш модуляция процесінде сигнал болады. Жіберетін хабарламағ а сә йкес уақ ытқ а ө згеретін, тасығ ыш параметрлері, ақ параттық деп аталады. Ақ паратты тасығ ыш ретінде ә ртү рлі табиғ и тербелістер пайдаланылады, кө бінесе гармоникалық. Техникалық ақ параттық жү йелерде тасығ ыш электрлік кернеу немесе тоқ тү рінде ең кө п тарағ ан.

Тасығ ышта u(t) = const тек бір ғ ана ақ параттық параметр болады – дең гей (мысалы, кернеу дең гейі). Гармоникалық электрлік тербелісті пайдалану кезінде амплитуда, жиілік, фаза сияқ ты параметрлер ақ параттық болуы мү мкін. Тербелісті детерминирленген жә не кездейсоқ деп екіге бө леді.

2-CҰ РАҚ – 20%

Жиынтық ты жә не ү здіксіз, ажыралатын жә не ажыралмайтын кедергіге шыдамды кодтарды сипаттаң ыз

Алгебралық кодтарды екі ү лкен кластарғ а бө лсе болады: жиынтық ты жә не ү здіксіз кодтар. Жиынтық ты кодтауда кодталатын ә рбір хабар ә рпіне k таң балар тізбегі сә йкес қ ойылады. Мұ нда тү рлендіру амалдарында тек қ ана k таң балары қ атысып, ал шығ у тізбегі жіберілетін хабардағ ы басқ а таң баларғ а байланысты болмайды. Жиынтық ты кодтар ажыралатын жә не ажыралмайтын деп бө лінеді. Ажыралатын кодтарда ақ параттық таң балар арна кодеріне келіп тү сетін ақ параттың таң балар тізбегі болып, ал артық ша немесе тексеруші таң баларды берілген тізбекке арна кодері қ ұ рып, ендіреді, бұ л қ ателікті анық тау жә не тү зету ү шін қ ызмететеді. Ажырамайтын кодтарда шығ у тізбегіндегі таң баларды ақ параттық жә не тексеруші деп ажыратып болмайды. Ү здіксіз кодтарда кодталатын ақ параттық таң баларды ендіру ү здіксіз орындалады жә не олар тә уелсіз жиынтық тарғ а ажыратылмайды.

3-СҰ РАҚ – 20%

Қ ателіктің дә режесі деп нені тү сінеміз?

Қ ателіктің дә режесі деп берілген ақ паратан кеткен қ ателік кө рсеткіші, оны анық тау Хэмминг кодымен анық тап жә не тү зетуге болады. Ал қ ателік дә режесі жоғ ары болғ анда оларды тү зету ү шін сызық ты кодтарды қ олдану тиімді болмайды, осындай болғ анда мажоритар қ ағ идада қ ұ рылғ ан декодтау қ ұ рылымдары анағ ұ рлым қ арапайым болады. Осы кезде мажоритарлық сұ лбада декодтаушы кө птеген кодтар бар, осындай кодтарды қ ұ рудың жаң а жолдары да жаратылғ ан.

4-СҰ РАҚ Есеп: - 40 %

300 детальдің ішінде 3 жарамсыз болу ық тималдығ ын табу керек?

1 элементтің жарамсыз болу ық тималдығ ы 0, 02 тең. P_n (k) =? P₃₀₀ (3) =?

Шешімі: n ө те ү лкен, ал p нің мә ні ө те кіші; сондық тан Пуассон тең деуін қ олданамыз: λ = 300 ● 0, 02=6;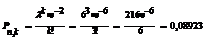

№4


D	E	B	B	B	E	A	A	C	A

1-сұ рақ Ақ параттық параметрлердің қ ұ рылымына байланысты сигналдар дискретті, ү зіліссіз жә не дискретті-ү зіліссіз болып бө лінеді

Детерминирленген сигнал бірлік шамағ а тең болатын уақ ыттың кез келген моментінде белгілі болжап білетін параметрлер мағ ынасы кездейсок тү рде берілген сигнал тү рі. Сигналды дискретті деп санайды егер осы параметр қ абылдайтын шама саны соң ғ ы болса (немесе саналғ ан). Егер параметрдің кө птеген мү мкін шамалары континуумды қ ұ рса, онда сигналды берілген параметр бойынша ү зіліссіз деп санайды. Сигнал, бір параметр бойынша дискретті ал келесі параметр бойыеша ү зіліссіз болса онда дискретті-ү зіліссіз деп аталады.

Қ арастырылып отырғ ан сигналдардың уақ ыттық функция тү ріндегі моделі сигнал формасының анализіне арналғ ан. Кү рделі сигналдар элементар сигналдардың жиынтығ ынан тұ рады. Зерттеуші жү йенің кең ауқ ымды класы – ол уақ ытқ а инвориантты сызық ты жү йелер. Детерминерленген сигналдың математикалық кө рсетілуі:

1. ү зіліссіз аргументтің ү зіліссіз функциясы. Мысалы: уақ ыттық ү зіліссі функциясы

2. дискретті аргументтің ү зіліссіз фнукциясы. Мысалы: уақ ыттың мә ні белгілі бір анық талғ ан моментінде ғ ана есептелген функция

3. ү зіліссіз аргументтің дискретті функциясы. Мысалы: дең гей бойынша кванттаудың уақ ыттық функциясы

4. дискретті аргументтің дискретті функциясы. Мысалы: белгілі бір моментінде мү мкін болатын кө п мә н қ абылдайтын функция.

2-CҰ РАҚ – 20%Минималды код қ ашық тығ ы қ алай табылады? Минималды код қ ашық тығ ы - бұ л кез-келген кодтық комбинация басқ асынан ажыратылатын элементтердің минималды саны. Мысалы, код мынандай комбинациялардан тұ рады: 1011, 1101, 1000 жә не 1100. Бірінші екі комбинацияны салыстыра отырып dmin=2 табамыз. Ең ү лкен шама dmin=3 бірінші жә не тө ртінші комбинацияларын салыстырғ анда табылады, ал ең кішісі dmin=1 екінші жә не тө ртінші, ү шінші жә не тө ртінші комбинацияларды салыстырғ анда табылады. Яғ ни минимал код қ ашық тығ ы дегеніміз барлық код қ исындастыруларының барлық жұ п бойынша қ осып шық қ анда олардың ішіндегі ең кемі. Минимал код қ ашық тығ ын табуда қ ателіктердің байланысты болмағ ан жағ дайына арналғ ан минимал қ ашық тық ты табу тең деуі сигналғ а байланысты қ ателіктерге қ арағ анда артық ғ ырақ мә ндер береді.

3-СҰ РАҚ – 20%Анық талатын жә не тү зетілетін қ ателіктер саны мен минималды код қ ашық тығ ы арасындағ ы қ атысты жазың ыз.

Екі код қ исындастыруының бірінен бірінің айырмашылығ ы Хэмминг мағ ынасындағ ы олардың арасындағ ы қ ашық тық пен немесе код қ ашық тығ ымен сипатталады. Ол код қ исындастыруларының бірінен бірінің айырмашылығ ы олардың ерекше таң балар санымен ө лшенеді жә не d белгіленеді. Минимал орынды код қ ұ ру ү шін (n, k) - кодта j бірінші ақ параттық таң баларды нө лдермен алмастырып жә не оларды код қ исындастыруынан шығ арып тастау керек болады. Бірақ мұ нда код циклдік болмайды, себебі мұ нда бір рұ қ сат етілген код қ исындастыруын циклдік жылжытқ анда сол кодтың басқ а рұ қ сат етілген код қ исындастыруы келіп шығ а бермейді.

4-СҰ РАҚ Есеп: - 40 %

Ү здіксіз хабарды дискереттегенде оның ә рбір дискреті 1 байтқ а жазылады; ө лшемдердің анық тығ ын 2 есе арттыру ү шін неше дә реже қ осу керек?

Шешімі: Ө лшемдердің анық тығ ын 2 есе арттыру ү шін 1 бит қ осу керек, яғ ни 9 бит болуы керек.

№5


A	D	C	D	D	B	A	D	A	A

1-сұ рақ Сигналдардың уақ ыттық формасы

Сигналдың уақ ыттық крсетілуі деп, базистік функция ретінде бірлікимпільстік функция немесе Δ функция қ оланылатын, уақ ыттық сигналғ атаратылуын айтады. Мұ ндай функцияның математикалық сипаттамасы: Мұ ндағ ы δ (t)-Δ функция

Δ функция кө мегімен тұ рақ ты немесе ө згермелі дең гейлі периодты тізбектіимпульс кө рсеткіштері болады. t=kΔ t нү ктелерінде уақ ыт функциясы U(kΔ t) тең жә не қ алғ а барлық жағ дайда нө лге тең. Осығ ан байланысты периодты уақ ыттың функциясы

4)Мұ ндағ ы Δ t- импульс жү ру қ адамы Сигнал ұ зақ тығ ы оның спектр ені соң ғ ы интервалмен шектелмейді. Егер сигнал

ұ зақ тығ ы шектелген болса, онда оның спектрі шектелмейді. Ал шектелгенспекртлі сигнал болса, керісінше оның ұ зақ тығ ы шексіз созылады. ∆ t∆ f=c Мұ ндағ ы ∆ t-импульс ұ зақ тығ ы ∆ f-импульс спектрінің ені С-импульс формасына тә уелді тұ рақ ты шама

t0 = 0 уақ ыт моментінде басталғ ан сигнал ү шін∫ | U(t) | 2 dt= η ∫ | U(t) | 2 dt (12)

η -(0. 9: 0. 99) ө згеретін коэффициен Парсеваль тепе-тең дік кө мегімен (10) сигнал спектр ені алынады:

1/π ∫ |S(ω )|2 dω = η /π ∫ |S(ω )|2 dω (13)

Орташа қ уат Рорт =lim 1/2π уақ ыт бойынша шектелген сигнал қ уаттың

спектрінің тығ ыздығ ыPkT(ω )= |S(ω )|2 /2π T (14

2-CҰ РАҚ – 20%Тү зетуші кодтың негізгі сипатты кө рсеткіштерін атаң ыз

Тү зету кодтары деп кодалық комбинациялардағ ы қ ателерді тү зете алатын жә не қ ателерді таба алатын кодтарды атайды. Олар екі топқ а бө лінеді: 1) табылғ ан қ ателер кодтары; 2) табылғ ан жә не тү зетілген қ ателер кодтары.

Табылғ ан қ ателер кодтарының ерекшелігі болып оның қ ұ рамындағ ы кодалық комбинциялардың бір-бірінен кем дегенде d=2–ге ажыратылатынында. Оларды шартты тү рде екі топқ а бө луге болады:

а) қ олданылатын комбинациялардың санын кеміту арқ ылы қ ұ рылғ ан кодтар.

Комбинациялардағ ы бірліктер жә не нө лдердің тұ рақ ты саны бар код.

б) барлық комбинациялар қ олданылатын, бірақ олардың ә р біреуіне белгіленген ереже бойынша бақ ылау символдары қ осылатын кодтар, m - символдар. Жұ птық қ а тексеретін кодтар. Бұ ндай тү р (неизбыточного) кодтың ақ параттық символдардан тұ ратын жіберіліп жатқ ан комбинацияғ а m (0 немесе 1) бақ ылау символын қ осу арқ ылы жү зеге асады. Жіберіліп жатқ ан комбинацияның бірліктерінің жалпы саны жұ п болу ү шін жасалады.

3-СҰ РАҚ – 20%Топтар, кіші топтар жә не жанасқ ан класстарғ а анық тама берің із

Топтар олар элементтер жиынынан қ ұ ралғ ан болып, онда бір негізгі операция анық талғ ан болады жә не де аксиомалар орындалады. Топтың кіші жиындары кіші топтар деп аталып, топта анық талғ ан амалдарғ а салыстырғ анда топтар болады. Мысалы, ү ш орынды код қ исындастыруының кіші жиыны: 000, 001, 010, 011 мысалда кө рсетілген ү ш орынды код қ исындастыруының кіші тобын қ ұ райды.

4-СҰ РАҚ Есеп: - 40 % Ү здіксіз хабарды дискреттегенде оның ә рбір дискреті 2 байтқ а жазылады; ө лшемдерді 1 байтқ а жазғ андағ ығ а қ арағ анда неще есе анық тық артады?

Шешімі: Q₂ = 2¹⁶= 65536 bit, Q₂ = 2⁸= 256 bit; Q₂/Q₁ = 65536/256= 256 есе артады. Демек ақ парат кө лемі 2 есе артқ анда, анық тық 256 есе артады.

№6


A	D	C	E	D	D	E	B	C	A

⇐ Предыдущая 123 4 5 6 7 Следующая ⇒