Результирующая A1 амплитуда вектора A1 плоской световой волны линии на Э экране посередине геометрической тени Щ щели с величиной d = d1 полуширины в непрозрачной 4 страница

изменении длины световой волны на δ λ величину, которая определяется из следующего соотношения: D_у = δ υ /δ λ . (10. 189) Элементарное δ (hsinυ _imax) приращение с использованием левой части (10. 149) при изменении υ _imax угла отклонения к главной оптической OZ оси Л линзы главного дифракционного максимума на элементарную δ υ величину имеет следующий вид:

δ (hsinυ _imax) = h(dsinυ /dυ )|_{υ =} _υ_i_maxδ υ = (hcosυ _imax)δ υ . (10. 190) Элементарное δ (hsinυ _imax) приращение с использованием правой части (10. 149) при изменении длины λ световой волны, распространяющейся (рис. 10. 37) от каждой из N щелей под υ _imax углом к главной оптической OZ оси Л линзы, на элементарную δ λ величину без учёта отрицательного знака в этой правой части имеет следующий вид: δ (hsinυ _imax) = δ (mλ ) = m(dλ /dλ )δ λ = mδ λ . (10. 191) Приравниваем (10. 190) и (10. 191) и получаем с учётом (1. 189) зависимость угловой D_у дисперсии ДР дифракционной решётки с учётом малых υ _imax углов отклонений к главной оптической OZ оси Л линзы главных дифракционных максимумов, поэтому cosυ _imax≈ 1, от номера порядка m =1, 2, 3, … дифракционных максимумов и h расстояния между щелями дифракционной решётки, которая имеет следующий вид:

(hcosυ _imax)δ υ = mδ λ ↔ δ υ /δ λ = m/(hcosυ _imax) ↔ D_у = m/(hcosυ _imax) ≈ m/h. (10. 192)

Линейная D_л дисперсия - это отношение приращения (рис. 10. 45) линейного δ l отклонения к главной оптической OZ оси Л линзы главного дифракционного максимума m - го порядка при изменении длины световой волны на δ λ величину, которая определяется из следующего соотношения: D_л = δ l/δ λ . (10. 193) C учётом (рис. 10. 45) малых υ _imax углов отклонений к главной оптической OZ оси Ллинзы главных дифракционных максимумов линейное δ l отклонение относительно этой главной оптической OZ оси Л линзы главного дифракционного максимума m - го порядка при изменении длины световой волны на δ λ величину определяется из следующего соотношения: δ l ≈ fδ υ . (10. 194) Подставляем (10. 194) в (10. 193) и получаем следующую зависимость D_л линейной дисперсии от f фокусного расстояния Л линзы, которое равно расстоянию от этой Л линзы до Э экрана, а также в зависимости от (10. 189) угловой D_у дисперсии ДР дифракционной решётки: D_л≈ fδ υ /δ λ ↔ D_л≈ fD_у. (10. 195) Подставляем (10. 192) выражение угловой D_у дисперсии ДР дифракционной решётки в (10. 197) и получаем следующую зависимость линейной D_л дисперсии от f фокусного расстояния Л линзы, которое равно расстоянию от этой Л линзы до Э экрана, а также в зависимости от номера порядка m =1, 2, 3, … дифракционных максимумов и h расстояниямежду щелями ДР дифракционной решётки: D_л≈ fm/h. (10. 196)

Угловая ширина главного дифракционного максимума нулевого порядка плоской монохроматической световой волны

От ДРдифракционной решётки (рис. 10. 37) вторичнаясферическая волна, имеющая световую волну с длиной λ , гдеλ = λ ₀ /n–длинасветовой волны в однородной изотропной среде с n показателем преломления, поэтому оптическаяλ = λ ₀ /nдлинаэтой световой волны совпадает с геометрическими размерами на рис. 10. 35, распространяется от каждой из N щелей, находящихся на h расстояниидруг от друга, под υ _min углом к главной оптическойOZ осиЛ линзы. Если υ _min ≈ ±λ /Nh, то с учётом малости υ _min угла к главной оптическойOZ оси Л линзы при дифракции имеет место следующее соотношение: sin ± υ _min = sin ± λ /Nh ≈ ± λ /Nh. (10. 197)

Подставляем (10. 197)в (10. 158) и получаем следующую I_{υ minN} интенсивность световой волны при распространении от ДР дифракционной решётки вторичной сферической волна под υ _min ≈ ±λ /Nh углом к главной оптической OZ оси Л линзы:

I_υ_minN ≈ I_d[sin²(π d/Nh)]/(π d/Nh)²][sin²π ]/[sin²(π /N)] = 0. (10. 198)

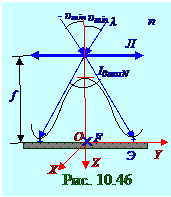
Согласно (10. 198) световая волна (рис. 10. 46)λ длиной, которая распространяется от каждой из N щелей, находящихся на h расстояниидруг от друга, под υ _min ≈ ±λ /Nh угломк главной оптической

OZ оси Л линзыобразует при (10. 163)значении m = 0 порядка главного дифракционного максимума слева и справа от него главные дифракционные минимумы. Угол Δ υ ₀_max между лучами

(рис. 10. 46) световой волны, направленными на главные дифракционные минимумы, является угловой шириной главного дифракционного максимума нулевого порядка с I₀_maxN интенсивность ю световой волны при (10. 161)значении m = 0 порядка главного дифракционного максимума, и эта Δ υ ₀_max угловая ширина главного дифракционного максимума нулевого порядка имеет следующее значение: Δ υ ₀_max = 2υ _min = 2λ /Nh. (10. 199)

Разрешающая способность дифракционной решёткипо критерию Релея

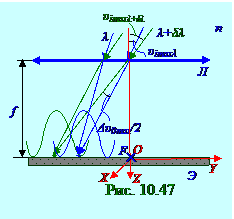
От ДР дифракционной решётки (рис. 10. 37) вторичная сферическая волна, имеющая световые волны с длинами λ и λ +δ λ , гдеλ = λ ₀ /n – длина световой волны в однородной изотропной среде с n показателем преломления, поэтому оптическая λ = λ ₀ /n длина этой световой волны совпадает с геометрическими размерами на рис. 10. 2. 0. 47, распространяется от каждой из N щелей, находящихся на h расстояниидруг от друга, под υ _imaxλ и υ _{imaxλ +δ λ} углами к главной оптической OZ оси

Л линзы.

Каждая световая волна с длинами λ и λ +δ λ образует на Э экране главные дифракционные максимумы c i - ыми значениями, под которыми производят наблюдение главных дифракционных максимумов m - ого порядка, имеющее одинаковое значение для этих λ и λ +δ λ длин световых волн.

Вследствие малости υ _imaxλ и υ _{imaxλ +δ λ}углов, под которыми наблюдаются на Э экране главные дифракционные максимумы m - ого порядка, справедливы следующие соотношения:

sinυ _imaxλ ≈ υ _imaxλ и sin υ _{maxλ +δ λ}≈ υ _{maxλ +δ λ}. (10. 200) По критерию Релея главные дифракционные максимумы m - ого порядка будут различимы, если центр этого главного дифракционного максимума m - ого порядка от световой волны с

λ длиной, имеющий υ _imaxλ угол к главной оптической OZ оси Л линзы, будет отстоять от главного дифракционного максимума того жеm - ого порядка световой волны с λ +δ λ длиной на угол, не

меньший, чем(10. 201) половина Δ υ ₀_max/2 = λ /Nh угловой ширины ( рис. 10. 35) главного дифракционного максимума нулевого порядка с I₀_maxN интенсивность ю световой волны.

Поэтому по критерию Релея главные дифракционные максимумы m - го порядка будут различимы, если υ _imaxλ и υ _{imaxλ +δ λ}углы, под которыми наблюдают главные дифракционные максимумы m - го порядка удовлетворяют соотношению:

υ _imaxλ_{+δ λ} - υ _imaxλ ≥ Δ υ _0max/2 ↔ υ _imaxλ_{+δ λ} - υ _imaxλ ≥ λ /Nh. (10. 201) где (10. 163) υ _imax, υ _{imaxλ +δ λ}- i - ое значение угла (рис. 10. 2. 0. 47) к главной оптической оси Л линзы, под которым при данных λ и λ +δ λ длинах световых волн наблюдаются главные дифракционные максимумы m - ого порядка, имеющее одинаковое значение для этих λ и λ +δ λ длин световых волн.

Для υ _imax, υ _{imaxλ +δ λ}углов согласно (10. 161) выполняются следующие условия: hsinυ _imax = ± mλ ; hsinυ _{imaxλ +δ λ} = ± m(λ +δ λ ). (10. 202) С учётом малости υ _maxλ и υ _maxλ_{+δ λ} углов, под которыми наблюдаются на Э экране главные дифракционные максимумы m - ого порядка, т. е. при условии выполнения условия (10. 202), положительныезначения этих υ _imaxλ и υ _imaxλ_{+δ λ} углов определятся из (10. 202) выражения: hsinυ _imaxλ = mλ ↔ υ _imaxλ ≈ mλ /h; hsinυ _imaxλ_{+δ λ} = m(λ +δ λ ) ↔ υ _imaxλ_{+δ λ} ≈ m(λ +δ λ )/h. (10. 203) Подставляем (10. 203) в (10. 201) и для определения минимальногоδ λ отклоненияот λ длины световойволны, при котором главные дифракционные максимумыm - ых порядков световыхволн с λ и λ +δ λ длинами будут по критериюРелея

различимы, заменяем неравенство в (10. 201) равенством и получаем следующее выражение R разрешающей способности дифракционной решётки:

[m(λ +δ λ )/h] - [mλ /h] = λ /Nh ↔ λ /δ λ = mN ↔ δ λ = λ /mN ↔ δ λ = λ /R, (10. 204) где δ λ - минимальная разность двух длин волн или двух спектральных линий, при которой после их прохождения дифракционной решётки образуются различимые по критерию Релея главные дифракционные максимумы; R = mN - разрешающая способность дифракционной решётки.

Согласно (10. 204) с увеличением порядка m - ого дифракционного максимума и количества N щелей в ДР дифракционной решётке уменьшается минимальная δ λ разность двух длин волн, которые по дифракционной картине воспринимаются по критерию Релея раздельно.

Дифракция рентгеновских лучей на линейных цепочках структурных элементов. Формулы Лауэ

На кристаллах, у которых b расстояниемежду структурными элементами, т. е. атомами, ионами, порядка 10^{-10 м}, условия дифракции выполняются для (10. 7) из раздела 10. 1 " Волновые свойства света " рентгеновских лучей с длинами волн 10^{-14 м <} λ < 10^{-7 м}. Линейная (рис. 10. 48)цепочка по OY оси структурных элементов, находящихся друг от друга на фиксированном h_y расстоянии или имеющих h_y период, при падении на неё параллельного пучка рентгеновских лучей под β ₀углом, возбуждает согласно принципу Гюйгенса - Френеля

(рис. 10. 15) из раздела 10. 1 " Волновые свойства света " вторичную сферическую волновую поверхность рентгеновских лучей, которые распространяются в верхнюю полусферу под разными углами и в том числе под β углом к OY оси.

Оптическая (рис. 10. 48) разность Δ _до хода лучей 1 и 2 в составе параллельного пучка рентгеновских лучей с плоским волновым фронтом в нижней полусфере до рассеяния на структурных элементах по аналогии с оптической(рис. 10. 37) Δ разностью хода между соседними световыми лучами на ДР дифракционной решётке имеетследующую величину, равную катету в прямоугольном треугольнике с h_y гипотенузой и β ₀ углом между ними: Δ _до= h_ycosβ ₀. (10. 205)

При этом 2 луч отстаёт по фазе от 1 луча.

После рассеяния параллельные 1′ и 2′ лучи, идущие под β углом к OY оси, имеют следующую оптическую разность Δ _послехода, равнуюповеличине катету в прямоугольном треугольнике с

h_y гипотенузой и β углом между ними: Δ _после = h_ycosβ . (10. 206)

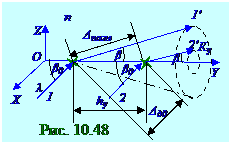
При этом 2′ луч опережает по фазе 1′ луч. Общая Δ ₀оптическая разность хода лучей 1′ и 2′ , находящихся на К_yбоковойповерхности (рис. 10. 37) конусас учётом Δ _дооптической разностей хода 1 и 2 лучейдо (10. 205) рассеяния и оптической Δ _после разностей хода 1′ и 2′ лучей после(10. 206) рассеяния, имеет следующий вид: Δ ₀= Δ _после- Δ _до = h_y(cosβ - cosβ ₀). (10. 207) Если Δ ₀общая (10. 209) оптическая разность хода 1′ и 2′ лучей,

находящихся на К_y боковой поверхности (рис. 10. 48) конуса, кратна λ длине волны рентгеновских лучей, то на этой К_y боковой поверхности конуса, будет наблюдаться их дифракционный максимум.

Таким образом, условием возникновения дифракционного максимума рентгеновских лучей с λ длиной волны на (рис. 10. 48) К_y боковой поверхности конуса является следующее выражение: Δ ₀= h_y(cosβ - cosβ ₀) = ±m_yλ , (10. 208) где m_y= ± 0, 1, 2, … - порядок дифракционного максимума на К_y боковой поверхности конуса, ось которого направлена по OY оси координат, соответствующий линейной цепочке структурных элементов по этой OY оси координат с h_y расстояниями между ними и дискретным значениям β ₀, β углов соответственно падения и рассеяниярентгеновских лучей с λ длиной волны, распространяющихся в однородной изотропной среде с n показателем преломления, поэтому оптическая λ = λ ₀ /n длина этой световой волны совпадает с геометрическими размерами на

рис. 10. 48. Знак " -" в номере m_y порядке дифракционного максимума соответствует случаю, когда (cosβ - cosβ ₀) разность в (10. 208) отрицательна.

Линейные (рис. 10. 49)цепочки по OX и OZ осям структурных элементов, находящихся друг от друга на фиксированных соответственно h_x и h_z расстояниях, при падении на них параллельных пучков рентгеновских лучей с λ длиной волны под α ₀ и γ ₀ углами образуют на К_x и К_z боковых поверхностях конусов c α и γ углами при вершине дифракционные максимумы по аналогии с

(рис. 10. 48) К_y боковой поверхности конуса.

Таким образом, условием возникновения дифракционных максимумов рентгеновских лучей с λ длиной волны на К_x и К_z боковых поверхностях конусов являются следующие выражения:

h_x(cosα - cosα ₀) = ± m_xλ ; h_z(cosγ - cosγ ₀) = ± m_zλ . (10. 209) где m_x; m_z = ± 0, 1, 2, … - порядки дифракционных максимумов на К_x и К_z боковых поверхностях конусов, оси которых направлены по соответственно осям OX и OZ осям координат; λ - длина волны рентгеновских лучей, распространяющихся в однородной изотропной среде с n показателем преломления, поэтому оптическая λ = λ ₀ /n длина этой световой волны совпадает с геометрическими размерами на рис. 10. 48.

Понятие о рентгеноструктурном анализе

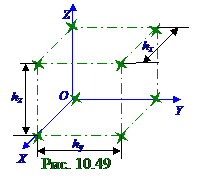
На поверхностях К_x, К_y и К_z конусовc α , β и γ углами при вершине (рис. 10. 49) рассеянныерентгеновские лучи с λ длиной волны образуют дифракционные максимумы на структурных элементах, которые представляют собой линейные цепочки по OX, OY и OZ осямс соответственно h_x, h_y и h_z периодами. Углы α , β и γ при вершине К_x, К_y и К_z боковыхповерхностях конусовсдифракционными максимумамирассчитываютсяпо формулам (10. 208), (10. 209) Лауэ при задании α ₀, β ₀ и γ ₀ углов падения параллельныхпучков рентгеновских лучей с λ длиной волны на структурные

элементы, которые представляют собой линейные цепочки по OX, OY и OZ осямс соответственно h_x, h_y и h_z периодами, и при задании m_x, m_y и m_z порядков дифракционных максимумов на этих К_x, К_y и К_z боковых поверхностях конусов.

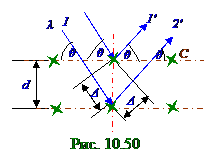
Рентгеновские лучи(рис. 10. 50)с λ длиной волны движутся под θ углом скольженияк C поверхности кристалла, в котором для простоты атомныеплоскости, т. е. плоскости, проведённые через узлы кристаллической решётки, совпадают и параллельныэтой Cповерхности кристалла. Расстояние между соседними атомнымиплоскостями равно d. Рентгеновские2 лучи(рис. 10. 50)с λ длиной волны падают

Дифракция рентгеновских лучей на совершенном кристалле, условие Брэгга – Вульфа

под θ углом скольжения от узла кристаллической решётки, который находится на C поверхности кристалла, и отражается от него под тем же θ углом скольжения. Рентгеновские 1 лучипадают на узел кристаллической решётки, находящегося на второй атомной плоскости, и отражаются от него под тем же, что и рентгеновские 2 лучи θ углом скольжения.

Оптическая разность хода между отражёнными 1' - ым и 2' - ым рентгеновскими лучами равняется следующим двум 2Δ катетам в прямоугольном треугольнике с гипотенузой, равной

d расстоянию между соседними атомными плоскостями: 2Δ = 2dsinθ . (10. 210) Если оптическая разность хода в (10. 210) между отражёнными 1' - ым и 2' - ым рентгеновскими лучами кратна целому числу λ длин волн, то по аналогии с дифракционными максимумами (10. 163) у световых волн в направлении θ угла скольжения этих отражённых рентгеновских лучей возникает дифракционный максимум. С учётом (10. 210) условие

Брэгга - Вульфа существования дифракционных максимумов у отражённых рентгеновских лучей, имеющих λ длину волны, в направлении θ угла скольжения от атомных плоскостей с d расстоянием между ними имеет следующий вид: 2dsinθ = mλ . (10. 211)

где m - целое число, принимающее значения 1, 2, 3, …, называемое порядком отражения.

⇐ Предыдущая 1 2 3 4 56