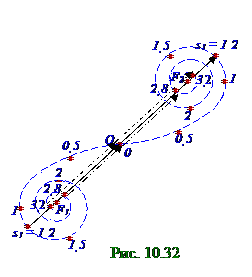
Результирующая A1 амплитуда вектора A1 плоской световой волны линии на Э экране посередине геометрической тени Щ щели с величиной d = d1 полуширины в непрозрачной 1 страница

Пл плоскости с y₀ координатой определится (рис. 10. 32) на спирали Корню суммой длины вектора A _1лев, направленного из точки с s₁ параметром в левой частиспирали Корню в O центр, и длины вектора A _1пр, направленного из O центра в точку с s₁ параметром в правой частиспирали Корню.

Таким образом, результирующая A₁амплитуда вектора A ₁ плоской световой волны линии на Э экране посередине геометрической тени Щ щели с величиной d полуширины в непрозрачной

Пл плоскости с y₀ координатой определится (рис. 10. 32) на спирали Корню длиной вектора

A ₁, направленного из точки с s₁= 1_,2 параметром в левой частиспирали Корню в точку с

s₁= 1_,2 параметром в правой частиспирали Корню.

Согласно (рис. 10. 32) амплитуда A₁ вектора A ₁ плоской световой волны линии на Э экране посередине геометрической тени Щ щели в непрозрачной Пл плоскости с y₀ координатой будет максимальна, т. е. при значении d = d₁ полуширины Щ щели, соответствующей (10. 114) равенству параметра s₁ спирали Корню величине 1_,2, т. е. s₁= 1_,2, на Э экране напротив середины Щ щели I_y₀₁интенсивность монохроматической плоской световой волны будет максимальна.

При (рис. 10. 31) увеличении d полуширины Щ щели до значения d = d₂, соответствующей (10. 114) равенству параметра s₂ спирали Корню(рис. 10. 32)величине 2_,8, т. е. s₂= 2_,8, на Э экране напротив середины Щ щели I_y₀₂интенсивность монохроматической плоской световой волны будет уменьшена по сравнению с I_y₀₁интенсивностью монохроматической плоской световой волны при значении d = d₁ полуширины Щ щели, соответствующей равенству параметра s₁ спирали Корню величине 1_,2, т. е. s₁= 1_,2.

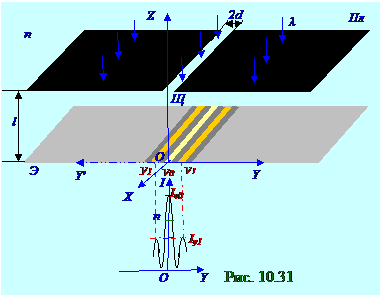
При (рис. 10. 31) увеличении d полуширины Щ щели до значения d = d₃, соответствующей (10. 114) равенству параметра s₃ спирали Корню(рис. 10. 32)величине 3_,2, т. е. s₃= 3_,2, на Э экране напротив середины Щ щели I_y₀₃интенсивность монохроматической плоской световой волны будет увеличена по сравнению с I_y₀₂интенсивностью монохроматической плоской световой волны при значении d = d₂ полуширины Щ щели, соответствующей равенству параметра s₂ спирали Корню величине 2_,8, т. е. s₁= 2_,8.

При (рис. 10. 31) увеличении d полуширины Щ щели до бесконечного значения, т. е. при удалении на пути монохроматической плоской световой волны бесконечной непрозрачной Пл плоскости, на Э экране будет существовать I₀интенсивность монохроматической плоской световой волны, которая падает нормально на этот Э экран. Интенсивность I₀ монохроматической плоской световой волны, которая падает нормально на Э экран, определяют по измерению длины вектора (рис. 10. 32), направленного из левого F₁фокуса спирали Корню в правый F₂фокус этой спирали Корню.

Таким образом, при дифракции Френеля (рис. 10. 31) на Э экране посередине геометрической тени Щ щели в непрозрачной Пл плоскости образуетсядифракционный максимум 0max (m = 0) нулевого порядка при определённых линейных размерах l расстояния Э экрана до непрозрачной Пл плоскости, длины λ нормально падающей на непрозрачную Пл плоскость световой волныи d полуширины Щ щели с уменьшающейсяинтенсивностьюсветовой волны по мере расширения этой d полуширины Щ щели.

Симметрично (рис. 10. 31) с двух сторон дифракционного максимума 0 max (m = 0) нулевого порядка при этих определённых линейных размерах l расстояния Э экрана до непрозрачной Пл плоскости, длины λ нормально падающей на непрозрачную Пл плоскость световой волныи d полуширины Щ щели образуются дифракционные максимумы 1max (m = 1) первого порядка при y₁ координате, 2 max (m = 2) второго порядка при y₂координате и т. д. с уменьшающейсяинтенсивностьюсветовой волны по мере увеличения расстояния от этих дифракционные максимумов до центра Щ щели.

Дифракция Фраунгофера световых волн от круглого отверстия

Монохроматическая плоская световая волна в однородной изотропной среде с

за единицу, и с величиной ø D диаметра примерно равного следующему значению: D ≈ f υ ₁_min, (10. 125) где f - фокусное расстояние Л линзы. Вокруг (рис. 10. 33) центрального светлогопятна с величиной ø D диаметра располагаются чередующиеся тёмные и светлые кольца. Первый дифракционный минимум образуется под υ ₁углом к OZ главнойоптической оси Л линзы, величина которого рассчитывается из следующего выражения: υ ₁_min= 1, 22λ /d. (10. 126) Выражение (10. 126) υ ₁_min угла первого дифракционного минимума при дифракции Фраунгофера монохроматической плоской световой волны от круглого отверстия применяется дляследующей оценки дифракционной δ θ расходимостипучка света в результате прохождения световой волной с λ длиной волнычерезДФдиафрагмусвеличиной ø d диаметра: δ θ ~ λ /d. (10. 127) Согласно выражению (10. 127)монохроматическая плоская световая волна с λ длиной волны после прохождения через ДФдиафрагмусвеличиной ø d диаметра перестаёт быть плоской, а лучи световой волны после прохождения через

n показателем преломления, поэтому оптическая λ = λ ₀ /n длина этой световой волны совпадает с геометрическими размерами на рис. 10. 33, падает нормально на ДФ диафрагму, в котором существует отверстие ø d диаметром, намного большим λ длины световой волны, т. е. ø d> > λ , а Э экран находится на большом удалении от этого отверстия. В этом случае на Э экране возникает дифракционная картина Фраунгофера, имеющая вид (рис. 10. 33) центрального светлогопятна I интенсивности, принятой за

υ ₂_max = =0, 004

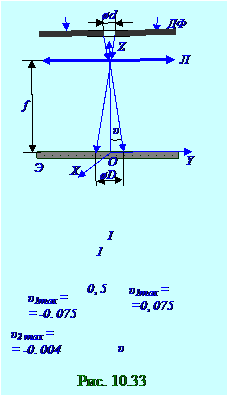
ДФ диафрагму распространяютсяв пределах конической поверхности с δ θ углом при вершине этого конуса. Величина (10. 127) дифракционной δ θ расходимости пучка света в результате прохождения световой волной с λ длиной волнычерезДФ диафрагму свеличиной ø d диаметра тем больше, чем меньше этот ø d диаметр ДФ диафрагмы.

Дифракция Фраунгофера световых волн от щели в плоскости

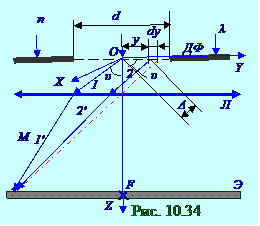
После прохожденияв однородной изотропной среде с n показателем преломления параллельным пучком световой волны с λ длиной ДФ диафрагмы, имеющей форму (рис. 10. 34) щели бесконечной длины по перпендикулярной плоскости чертежа OX осии d шириной по OY оси, возникает дифракция Фраунгофера. Каждый элементарный участок dy длиной плоской световой волны, находящийся на расстоянии y от центра O щели, согласно принципу Гюйгенса - Френеля

(рис. 10. 34), является источником вторичной сферической волны.

От элементарного (рис. 10. 34)участка длиной dy, находящегося в центре щели по OY оси, в котором находится O начало декартовой OXYZ системы координат, световые лучи распространяютсяв полупространство ниже OY оси под всевозможными углами к OZ главной оптической оси Л линзы и в том числе распространяется 1 луч под υ углом. От элементарного участка dy длиной, находящегося на расстоянии y от O центра щели, световой 2 луч тоже распространяетсяпод υ углом, но имеетследующую оптическую Δ разность хода относительно 1 луча: Δ = ysinυ . (10. 128)

Направим r радиус - вектор из (10. 8) выражения связи A проекции A светового вектора с

r модулем этого r радиус - вектора из O центра щ ели (рис. 10. 34) по световому 1 лучу. Каждый из лучей, параллельный световому 1 лучу, от элементарных участков dy длиной на всей ширине

d щели слеваи справа от её O центра на y расстоянии будут иметь следующую Ф_υ фазу (10. 18)

колебаний d A_υ светового вектора световой волны в произвольный момент t времени в M точке на

Э экране: Ф_υ = ω t - k(r₀+ Δ ) + φ , (10. 129) где r₀ - оптический путь, проходимый световой волной от элементарного участка dy длиной, находящегося в O центре щели, до M точки на Э экране; k = 2π /λ - волновое число, где

λ = λ ₀ /n – длина световой волны в однородной изотропной среде с n показателем преломления, поэтому оптическая λ = λ ₀ /n длина этой световой волны совпадает с геометрическими размерами

на рис. 10. 34. Положим начальную Ф_{υ 0} фазу(10. 126) световой волны в M точке на Э экране в момент t₀ = 0 времениот элементарного участка dy длиной, находящегося в O центре щели, равной нулю, поэтомус учётом (10. 130) равенства нулюоптической Δ ₀ разности ходапри y = 0, т. е. Δ ₀= 0 выражение φ начальной фазыколебанийA светового вектора монохроматическойплоской световой волны с λ длиной волны после прохождения (рис. 10. 34) черезДФдиафрагму принимает следующий вид: Ф_{υ 0} = ω t₀- k(r₀+ Δ ₀) + φ = 0 ↔ φ = kr₀. (10. 130) Подставляем (10. 128), (10. 130) в (10. 129) и получаем

следующую зависимость Ф_υ фазы колебаний d A_υ светового вектора световой волны в произвольный момент t времени в M точке на Э экране от любого из элементарных участков dy длиной на всей

d ширинещели слеваи справа от её O центра на y расстоянии с учётомk = 2π /λ волнового числа: Ф_υ = ω t - (2π /λ )ysinυ . (10. 131)

Угол υ , под которым падают световые лучи на Э экран от любого из элементарных участков dy длиной на всей d ширине щели, мал, поэтому A_dy амплитуда световой волны на Э экране не будет зависеть от направления падения световых лучей на этот Э экран, т. е. не будет зависеть от υ угла, а будет зависеть только от dy длины элементарного участка, вследствие чего эта A_dy амплитуда световой волны на Э экране имеет следующий вид: A_dy = (A_d/d)dy, (10. 132) где A_d - амплитуда вектора A светового вектора световой волны на Э экране от всей щели

d шириной; A_d/d - амплитуда A светового вектора световой волны на Э экране от единицы длины щели.

С учётом выражения (10. 8) связи Aпроекции A светового вектора с r модулемэтого r радиус - вектора в произвольный момент t времени в M точке на Э экране, т. е. под υ углом (рис. 10. 34)

к OZ главной оптической оси Л линзы, от элементарного участка щели dy длиной, а также с учётом (10. 132) A_dy амплитуды и (10. 133) Ф_υ фазы dA_υ модуль d A_υ светового вектора световой волны имеет следующий вид: dA_υ = (A_d/d)dycos[ω t - (2π /λ )ysinυ ], (10. 133) Модуль A_υ результирующего A светового вектора световой волны в произвольный момент

t времени в M точке на Э экране, т. е. под υ углом (рис. 10. 34) к OZ главной оптической оси

Л линзы, от всех элементарных участков щели dy длиной с предельными значениями y координат, изменяющихся от -d/2 до d/2 величин, имеет следующий вид: d/2

A_υ=∫ (A_d/d)cos[ω t -(2π /λ )ysinυ ]dy =

d/2 d/2 -d/2

=(A_d/d){ ∫ (cosω t)[cos(2π /λ )ysinυ ]dy+∫ (sinω t)[sin(2π /λ )ysinυ ]dy}=[A_dsin(π dsinυ /λ )cosω t]/(π dsinυ /λ ). (10. 134)

-d/2 -d/2

Амплитуда A_υ_m результирующего A светового вектора световой волны (рис. 10. 34) в

M точке на Э экране, т. е. под υ углом к OZ главной оптической оси Л линзы, с учётом (10. 136) выражения имеет следующий вид: A_υ = [A_dsin(π dsinυ /λ )]/(π dsinυ /λ ). (10. 135) В (рис. 10. 34) направлении OZ главной оптической оси Л линзы, т. е. когда угол υ → 0 и выражен в радианах, с учётом значения предела lim sin(π dsinυ /λ )cosω t/(π dsinυ /λ ) = 1 выражение (10. 135) принимает следующий вид: A|_{υ → 0} = A_d. (10. 136) Согласно (10. 136) в направлении OZ главной оптической оси Л линзы A|_{υ → 0} амплитуда результирующего A_υ светового вектора световой волны в центре Э экрана равна A_d амплитуде

A светового вектора световой волны на Э экране от всей щели d шириной.

Интенсивность(10. 17) I_υсветовойволны, пропорциональнаквадрату A_υ²амплитуды результирующего A_υ светового вектора световой волны (рис. 10. 34) в M точке на Э экране, т. е. под υ углом к OZ главной оптической осиЛ линзы, поэтому с учётом (10. 137) эта интенсивность I_υсветовойволны имеет следующий вид: I_υ = I_dsin²[(π dsinυ )/λ ]/[(π dsinυ )/λ ]², (10. 138) где I_d - интенсивность(рис. 10. 1. 0. 35)световойволны в центреЭ экрана. Дифракционные минимумы1min, т. е. 1-гопорядка, образуются при υ ₁_min углах отклонений (рис. 10. 34) плоской световой волны от OZ главной оптической осиЛ линзысогласно (10. 137) при m = 1,

При значениях υ угла к главной оптической оси Л линзы, удовлетворяющих следующему условию: π dsinυ /λ = ± mπ ↔ dsinυ = ± mλ , (10. 137) где m = 1, 2, 3, … амплитуда A_υ результирующего A светового вектора световой волны согласно (11. 137) обращается в нуль. Следовательно, в (рис. 10. 34) направлениях к OZ главной оптической оси Л линзы, где υ угол удовлетворяет условию (10. 139), световые волны от щели образуют дифракционные минимумы.

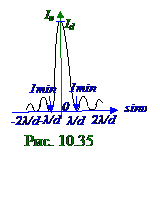
поэтому для этих дифракционных минимумов 1min, т. е. 1-го порядка, выражение(10. 139) принимает следующий вид: dsinυ ₁_min = ± λ ↔ δ υ = 2arcsin(λ /d), (10. 139) где δ υ - угловая ширина центрального дифракционного максимума, т. е. угол δ υ , выраженный в радианах, между двумя (рис. 10. 34) световыми лучами, симметричными относительно

OZ главной оптической оси Л линзы и направленными на дифракционные минимумы

(рис. 10. 35) 1min, т. е. 1-го порядка. Учтём в (10. 137) свойство тригонометрической функции sinυ ≤ 1 для её положительных значений, вследствие чего получим следующее выражение: dsinυ ≤ d ↔ mλ ≤ d ↔ d ≥ kλ , (10. 140) где m = 1, 2, 3, …. Согласно (10. 140) дифракционные максимумы и минимумы образуются, когда d ширина щели больше длины λ волны. В противном случае дифракционные максимумы и минимумы не возникают, а интенсивность I светамонотонно убывает от середины дифракционной картины к её краям. В случае d > > λ , т. е. λ /d < < 1 значение arcsin(λ /d) ≈ λ /d, поэтому угловую ширину δ υ центрального дифракционного максимума с учётом (10. 139) определяют согласно следующему выражению: δ υ = 2λ /d. (10. 141)

Предельный переход от волновой оптики к геометрической

При дифракции Френеля после прохождения(рис. 10. 36) параллельным пучком световой волны в однородной изотропной среде с n показателем преломления ДФ диафрагмы, имеющей форму щели бесконечной длины по перпендикулярной плоскости чертежа OX осии d шириной по OY оси, эта ДФ диафрагма открывает для M точки на Э экранеm количество зонФренеля, последний

m номер которых определяется из следующего выражения для прямоугольного OMK треугольника: (b + mλ /2)² = b² + (d/2)² ↔ (mλ /2)² + 2b(mλ /2) = d²/4. (10. 142) где d/2 - радиус последнейоткрытой для M точки на Э экранезоныФренеля, т. е. имеющей наибольший m номер открытой зоныФренеля, которая на рис. 10. 17 обозначена r_m радиусом; λ = λ ₀/n – - длина световой волны в однородной изотропной среде с n показателем преломления, поэтому оптическая λ = λ ₀/n длина этой световой волны совпадает с геометрическими размерами на рис. 10. 34.

По аналогии с (10. 94), ограничившись рассмотрением не слишком больших m номеров зонФренеля, можно ввиду малости λ длины световой волны пренебречь в (10. 130) слагаемым, содержащим λ ², вследствие чего получается следующее выражение для m номеров зонФренеля: 2b(mλ /2) ≈ d²/4 ↔ m ≈ d²/4λ b ↔ m ~ d/(λ b)^1/2. (10. 143) При количестве m < < 1 зонФренеля, что приводит в (10. 143) к d < < (λ b)^1/2выражению, щель настолько узкая, что открывает малую долю (рис. 10. 16) 1 - ой зоныФренеля с r₁радиусом. Поэтому дифракция Френеля отсутствует, т. к. каждый из световых лучей приходит на Э экран

с различием оптических путей намного меньших половины λ /2 длины волны. При: m < < 1 ↔ d/(λ b)^1/2 < < 1 ↔ d < < (λ b)^1/2(10. 144) наблюдается дифракция Фраунгофера на (рис. 10. 34), (рис. 10. 1. 0. 36) щели бесконечной длины по перпендикулярной плоскости чертежа OX осии d шириной по OY оси с (рис. 10. 1. 35) ярким центральным максимумом и бледными максимумами высших порядков.

⇐ Предыдущая 1 234 5 6 Следующая ⇒