Результирующая A1 амплитуда вектора A1 плоской световой волны линии на Э экране посередине геометрической тени Щ щели с величиной d = d1 полуширины в непрозрачной 2 страница

Если m = 1…5, что приводит в (10. 143) к d ≈ (1…5)(λ b)^1/2выражению, т. е. щель открывает небольшое

количество (рис. 10. 16) зонФренеля с r₁, …, r₅радиусами, то на Э экране существует (рис. 10. 19), (рис. 10. 20) дифракцияФренеляс изображением щели, обрамлённой по краям отчётливо видимыми светлымии тёмнымиполосами. При: m = 1…5 ↔ d/(λ b)^{1/ 2}≈ 1…5 ↔ d ≈ (1…5)(λ b)^1/2(10. 145) наблюдаетсяна Э экране (рис. 10. 17), (рис. 10. 18) дифракцияФренеляпосередине геометрической тени щели в ДФдиафрагме, обрамлённой по краям отчётливо видимыми светлымии тёмнымиполосами.

Если m > > 1, что приводит в (10. 143) к d > > (λ b)^1/2выражению, то щель открывает большое количество (рис. 10. 16) зонФренеля с r₁, r₂, r₃, …радиусами. На Э экране из-за большого

m количества зонФренеляА_m амплитуда световой волныот последней зоны с m номером, будет намного меньше, чем А₁амплитуда световой волныот 1 - ой зоныФренеля с r₁ радиусом из-за того, что расстояние от последней зоныФренеля с m номером будет намного больше расстояния от

1 - ой зоныФренеля с r₁радиусом. Поэтому в (10. 91) слагаемым А_m/2 можно пренебречь по сравнению с А₁/2, что является признаком отсутствия дифракции Френеля. На Э экране в этом случае получается равномерно освещённое изображение щели, которое строится по законам геометрической оптики.

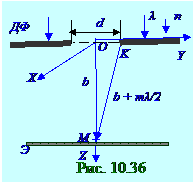
При: m > > 1 ↔ d/(λ b)^{1/ 2}> > 1 ↔ d > > (λ b)^1/2(10. 146) на Э экране получается равномерно освещённое изображение щели, которое строится по законам геометрической оптики. Из (10. 144), (10. 145) и (10. 146) критерием применимости либо законов геометрической оптики, либо дифракции Френеля, либо дифракции Фраунгофераявляется не малость λ длины световой волны в однородной изотропной среде с n показателем преломления по сравнению с характерным размером преграды, например, (рис. 10. 36) d шириной щели, а значение (10. 143)

m параметра, т. е. количества зонФренеля, открываемых этой преградой на Э экране.

Формирование дифракционной картины при нормальном падении на дифракционную решётку плоской монохроматической проходящей световой волны

Для осуществления многолучевой интерференции световых волн с близкими или равными

A амплитудами A световых векторов применяют специальные интерференционные приборы, например, дифракционную решётку.

После прохождения параллельным пучком световой волныв однородной изотропной среде с

n показателем преломления нормально поверхности ДР дифракционной решётки, имеющей форму (рис. 10. 34) щелей бесконечной длины по перпендикулярной плоскости чертежа OX оси, d шириной по OY оси и h расстоянием между щелями, I_υ интенсивность световой волныв произвольный момент t времени в M точке на Э экране, т. е. под υ углом к главной оптической оси Л линзы, определяется из (10. 138) выражения дифракции Фраунгоферанащелиdшириной.

Дифракционная решётка ДР имеет N щелей, поэтому вторичная сферическая волна, распространяющаяся параллельным пучком от каждой из этих N щелей под υ углом к главной оптической OZ оси Л линзы фокусируется этой Л линзойв её фокальной плоскости в M точке на

Э экране.

По аналогии (рис. 10. 34) с выражением (10. 128) из раздела 10. 1 " Волновые свойства света " оптической Δ разности хода двух параллельных лучей, отстоящихдруг от другана h расстоянии и имеющих υ угол между направлением лучей и оптической OZ осью

Л линзы, оптическая(рис. 10. 37) Δ разность хода между соседними из N световых лучей на Э экране имеет следующий вид: Δ = hsinυ , (10. 147) где h - расстояние между щелями, т. е. постоянная ДР дифракционной решётки.

Разность δ фаз между соседними из N световых лучей на Э экране с учётом их оптической (10. 147) Δ разности хода в однородной изотропной среде с

n показателем преломления имеет следующий вид: δ = 2π Δ /λ = (2π /λ )hsinυ . (10. 148)

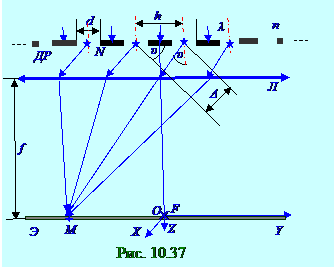
где λ - длинасветовой волны в изотропной среде с n показателем преломления, поэтому оптическаяλ = λ ₀ /nдлинаэтой световой волны совпадает с геометрическими размерами на рис. 10. 37. Векторы A_υ амплитуды световых векторов от соседних световых волн имеют равные A_υ модули, т. к. их оптические путираспространенияот каждой из N щелейдоM точки на Э экране, т. е. под υ углом к главной оптической осиЛ линзы, одинаковы. Разность(10. 148) Ф_υ_k+1- Ф_υ_k = δ фазмеждувекторами A_υ амплитудсветовых векторов от k+1-ой исоседнейk-ой щелями ДРдифракционной(рис. 10. 37) решёткиу

световых лучей, распространяющихся параллельным пучком от каждой из N щелей под υ углом к главной оптической OY оси Л линзы, одинакова и равна следующей постоянной величине: Ф_υ_k+1- Ф_υ_k = δ = const. (10. 149)

Согласно представлению гармонических колебаний на векторной диаграмме (рис. 2. 3)из раздела 2. 0 " Колебания и волны " результирующий вектор A_υ_рсветовых векторов от всех N щелей будет равен сумме векторов A_υ амплитуды светового вектора от каждой из N щелей до M точки на Э экране, т. е. под υ углом к главной оптической оси Л линзы.

Если количество (рис. 10. 37) щелей N₁, то результирующий вектор A_{υ N}₁амплитуды световых векторов от всех N₁ щелей будет равен сумме векторов A_υ амплитуды светового вектора от каждой из N₁ щелей доM точки на Э экране, т. е. под υ углом к главной оптической оси Л линзы.

Графически (рис. 10. 38) этот результирующий вектор A_{υ N}₁ определится суммой, например, 3 - х векторов A_υ, направленных под δ углом друг к другу и являющихся основаниями равнобедренных треугольников с δ углами между равными OO₁сторонами.

В равнобедренном треугольнике с основанием, равным модулю A_υ вектора A_υ амплитуды светового вектора от (рис. 10. 37) каждой из N₁ щелей, и δ углом при вершинеэтого равнобедренного треугольника, равным (рис. 10. 38) разности (10. 148)δ фаз между векторами A_υ амплитуд светового вектора от соседних щелей ДР дифракционной решётки, длина OO₁стороны имеет следующий вид: OO₁=(A_υ/2)/|sin(δ /2)|. (10. 150) Модуль A_{υ N}₁ результирующего вектора A_{υ N}₁амплитуды световых векторов от всех

N₁ щелей определится из равнобедренного треугольника, основанием которого является этот результирующий вектор A_{υ N}₁, а α ₁ уголпри вершине этого равнобедренного треугольника имеет следующий вид: α ₁ = N₁δ . (10. 151)

Для случая (рис. 10. 38) N₁= 3, т. е. 3 - х щелей у ДР дифракционной решётки, A_{υ N}₁ модуль

A_{υ N}₁ результирующего вектора с учётом (10. 151) имеет следующий вид:

A_{υ N}₁ = 2OO₁|sin(α ₁/2)| = 2OO₁ |sin(N₁δ /2)|. (10. 152)

Подставляем (10. 150) в (10. 152) и получаем следующее значение A_{υ N}₁ модуля результирующего вектора A_{υ N}₁амплитуды световых векторов от всех N₁ щелей в M точке (рис. 10. 37) на Э экране, т. е. под υ углом к главной оптической оси Л линзы:

A_{υ N}₁ = A_υ|[sin(N₁δ /2)]/[sin(δ /2)]|, (10. 153) где (10. 135) A_υ - амплитуда A светового вектора световой волны от одной щели (рис. 10. 35) в M точке на Э экране, т. е. под υ углом к главной оптической оси Л линзы.

под этим υ углом к главной оптической осиЛ линзыи этого числа N₂щелейу ДРдифракционнойрешётки. При увеличении числа Nщелей (рис. 10. 38) до величины N₃, например, до 6 -ти модуль A_{υ N}₃результирующего вектора A_υ_N3амплитуды световых векторов от всех N₃ щелейв M точке (рис. 10. 37) на Э экране, т. е. под υ углом к главной оптической осиЛ линзы, с учётом (10. 152) принимает следующий вид: A_{υ N}₃ = 2OO₁| sin(α ₂/2)| = 2OO₁|sin[π - (N₃δ /2)]| = = 2OO₁|sin(N₃δ /2)| = A_υ|[sin(N₃δ /2)]/[sin(δ /2)]|. (10. 154) По сравнению с A_{υ max}модулем при числе N₂щелей, например (рис. 10. 38), равным 4 -ём, модульA_{υ N}₃ результирующего вектора A_υ_N3амплитуды световых векторов от всех N₃ щелейв M точке (рис. 10. 37) на Э экране, т. е. под υ углом к главной оптической оси Л линзы, стал меньше.

Согласно (рис. 10. 38) при увеличении числа N щелей, например, до 4 -х угол α ₁/2 = (N₁δ /2) становится равным π /2 и модульA_{υ max} результирующего вектора A_{υ N}₂амплитуды световых векторов от всех N₂ щелей в M точке (рис. 10. 37) на Э экране, т. е. под υ углом к главной оптической оси Л линзы, становится максимальным, что означает существование дифракционного максимума на Э экране

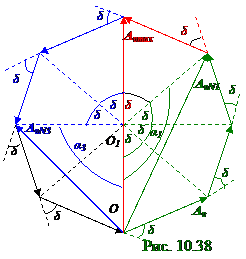
При числе N щелей, например (рис. 10. 38), равным 8 - ми, модуль A_{υ min} результирующего вектора A ₂_min амплитуды световых векторов от всех N щелей в M точке (рис. 10. 37) на Э экране, т. е. под υ углом к главной оптической оси Л линзы, становится равным нулю, что означает существование дифракционного минимума на Э экране под этим υ углом к главной оптической оси Л линзыи этого числа N щелей у ДР дифракционной решётки.

Из сравнения (10. 155) и (10. 156) при произвольном значении числа N щелей A_{υ N} модуль результирующего вектора A_{υ N} амплитуды световых векторов от всех N щелей в M точке

(рис. 10. 37) на Э экране, т. е. под υ углом к главной оптической оси Л линзы, имеет следующий вид: A_{υ N} = A_υ|[sin(Nδ /2)]/[sin(δ /2)]|. (10. 155) По аналогии с (10. 138) I_{υ N} интенсивность световой волны после прохождения параллельным пучком ДР дифракционной решётки с N щелямипропорциональна квадрату A_{υ N} ² амплитуды результирующего вектора A_{υ N} амплитуды световых векторов в M точке (рис. 10. 37) на Э экране, т. е. под υ углом к главной оптической оси Л линзы, и эта I_{υ N} интенсивность световой волны с учётом (10. 155) имеет следующий вид: I_{υ N} = I_υ [sin²(Nδ /2)]/ [sin²(δ /2)], (10. 156) где I_υ - интенсивность световой волны от одной щели (рис. 10. 35) в M точке (рис. 10. 37) на Э экране, т. е. под υ углом к главной оптической оси Л линзы.

Подставляем (10. 138) интенсивность световой волны от одной щели (рис. 10. 32) в M точке на Э экране, т. е. под υ углом к главной оптической оси Л линзы, в (10. 156) и получаем следующее выражениеI_{υ N} интенсивности световой волны после прохождения параллельным пучком ДР дифракционной решётки с N щелями:

I_{υ N} = I_dsin²[(π dsinυ )/λ ]/[(π dsinυ )/λ ]²[sin²(Nδ /2)]/ [sin²(δ /2)], (10. 157) где I_d - интенсивность (рис. 10. 37) световой волны после прохождения параллельным пучком одной щели d шириной в центре Э экрана. Подставляем (10. 148) разность δ фаз между соседними световыми лучами с λ длиной волны в (10. 157) и получаем следующее выражение I_{υ N} интенсивности световой волны после прохождения параллельным пучком дифракционной ДР решётки с N щелями d шириной, расстояние между которыми равно h, под (рис. 10. 37) υ углом к главной оптической оси Л линзы: I_{υ N} = I_d[ sin²(π dsinυ /λ )]/(π dsinυ /λ )²] [sin²(Nπ hsinυ /λ )]/[sin²(π hsinυ /λ )]. (10. 158) Второй сомножитель в (10. 158) имеет следующий предел: lim[sin²(Nπ hsinυ /λ )/sin²(π hsinυ /λ )] = N². (10. 159) |hsinυ | → mλ, где m = 0, 1, 2, … Согласно (10. 158) интенсивность I_{υ maxN} световой волны после прохождения параллельным пучком ДР дифракционной решётки с N щелями d шириной, расстояние между которыми равно h, под (рис. 10. 37) υ _max углом к главной оптической оси Л линзыимеет следующий вид: I_{υ maxN} = I_d[ sin²(π dsinυ _max /λ )]/(π dsinυ _max /λ )²] N²_,(10. 160) если υ _max угол к главной оптической оси Л линзы, под которым производят наблюдение дифракционной картины (рис. 10. 37) на Э экране удовлетворяет следующему условию:

hsinυ _imax = ± mλ , (10. 161) где υ _imax- i - ое значение угла (рис. 10. 37) к главной оптической оси Л линзы, под которым при данной λ длине волны производят наблюдение главного дифракционного максимума m - ого порядка.

На Э экране (рис. 10. 37) после прохождения параллельным пучком ДР дифракционной решётки с N щелями d шириной, расстояние между которыми равно h, под υ _max углом (10. 161) к главной оптической оси Л линзы колебания A световых векторов световой волны от отдельных щелей взаимно усиливают друг друга. Поэтому m число в условии (10. 161) определяет порядок главных дифракционных максимумов.

При (10. 161) m = 0 и следовательно при υ ₀_max = 0 наблюдают (рис. 10. 37) дифракционный максимум нулевого порядка на Э экране в 0 начале координат. Дифракционных максимумов

1-го, 2-го, 3-го и т. д. порядков имеется по два при (10. 161) соответственно m = 1 и m = -1, m = 2

и m = -2, m = 3 и m = -3 и т. д.

Согласно (10. 161)для дифракционных максимумов 1-го, 2-го и т. д. порядков, которые наблюдаются на Э экране под υ _i_max углами к главной оптической оси Л линзы справедливо следующее соотношение: |sinυ _imax| = mλ /h. (10. 162) По свойствам тригонометрической функции справедливо следующее соотношение:

|sinυ _imax| ≤ 1. (10. 163) Подставляем (10. 162) в (10. 163) и получаем следующиезначения m_в порядков главных дифракционных максимумов, которые возможно наблюдать в дифракционной картине:

m_вλ /h ≤ 1 ↔ m_в ≤ h/λ . (10. 164)

Формирование дифракционной картины при наклонном падении на дифракционную решётку плоской монохроматической проходящей световой волны

После прохождения параллельным пучком световой волныв однородной изотропной среде с

n показателем преломления (рис. 10. 39) под +θ углом падения на поверхность

ДР дифракционной решётки, имеющей форму щелей бесконечной длины по перпендикулярной плоскости чертежа OX оси, d шириной по OY оси и h расстоянием между щелями, оптическая Δ _{+υ -}_m разность хода двух параллельных лучей, отстоящихдруг от друга на h расстоянии и имеющих

+υ _-_m угол между направлением лучей и нормалью к поверхности ДР дифракционной решётки имеет с учётом (10. 147) следующий вид: Δ _{+υ -}_m= hsin+υ _-_m, (10. 165)

где знак " +" плюс означает, что υ _-_m угол отсчитывается от нормали к поверхности

ДР дифракционной решётки по " часовой стрелке" .

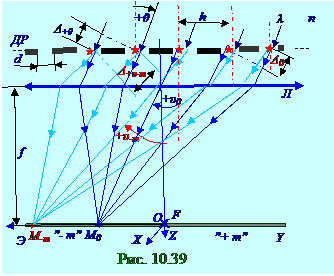
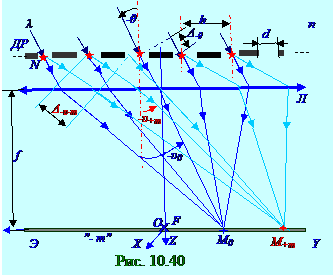
Оптическая Δ _+θразность хода двух параллельных лучей, падающих (рис. 10. 39) под

+θ угломотносительно нормали к поверхности ДР дифракционной решётки, отстоящимидруг от друга на h расстоянии, имеет с учётом (10. 147) следующий вид: Δ _+θ = hsin(+θ ). (10. 166) Общая оптическая Δ _o+θразность хода двух параллельных лучей, падающих (рис. 10. 39) под

+θ угломотносительно нормали к поверхности ДР дифракционной решётки, и выходящих из

N щелей в виде вторичной сферическая волна под +υ _-_m углом, имеет с учётом (10. 165), (10. 166) следующий вид: Δ _o+θ = Δ _+θ - Δ _{+υ -}_m = hsin(+θ ) - hsin(+υ _-_m), (10. 167) где знак " -" минус присутствует, потому что верхний из падающих (рис. 10. 39) под

+θ угломотносительно нормали к поверхности ДР дифракционной решётки световых лучей на величину Δ _+θ имеет бό льшую оптическую длину по сравнению с нижним световым лучом, а верхний из выходящих из N щелей в виде вторичной сферической волны под +υ _-_m углом световых лучей на величину Δ _{+υ -}_m имеет меньшую оптическую длину по сравнению с нижним световым лучом.

Условие наблюдение главного дифракционного максимума m - ого порядка (рис. 10. 39) на

Э экране от прохождения параллельным пучком световой волныв однородной изотропной среде с

n показателем преломления под +θ углом падения на поверхность ДР дифракционной решётки, имеет с учётом (10. 167) следующий вид: Δ _o+θ = hsin(+θ ) - hsinυ _imax= ± mλ , (10. 168)

где υ _imax- i - ое значение угла к главной оптической оси Л линзы, под которым при данной λ длине волны производят наблюдение главного дифракционного максимума m - ого порядка.

Условие наблюдение главного дифракционного максимума 0 - ого порядка (рис. 10. 39) на

Э экране от прохождения параллельным пучком световой волныв однородной изотропной среде с

n показателем преломления под +θ углом падения на поверхность ДР дифракционной решётки, имеет с учётом (10. 168) следующий вид: Δ _o+θ = hsin(+θ ) - hsin(+υ ₀) = 0 ↔ +θ =+υ ₀, (10. 169)

где+υ ₀ - значение угла к главной оптической оси Л линзы, под которым при данной λ длине волны производят наблюдение главного дифракционного максимума 0 - ого порядка, которое равно +θ углу падения на поверхность ДР дифракционной решётки параллельного пучка световой волныв однородной изотропной среде с n показателем преломления.

⇐ Предыдущая 1 2 345 6 Следующая ⇒