
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
2. Түйін арқылы түйінді ауыстыру қосымша түрлендірулерсіз-ақ жүзеге
2. Тү йін арқ ылы тү йінді ауыстыру қ осымша тү рлендірулерсіз-ақ жү зеге
асырылады.
3. Сумматорды ауыстыру. Егер сумматорды сигналдың берілісбағ ытына қ арсы беріліс функциясы ( ) 1 W s буын арқ ылы ауыстырсақ, сумматор менсыртқ ы ә сердің ортасына қ осымша буын қ осылады. Берілісфункциясы 1/ W1(s) тең болады (23 сурет). беріліс функциясы W1(s) буынның кірісіндегі сыртқ ы ә серді f шығ ысына ауыстыруғ а болады, буынның кірісі мен ә серарасына берілісфункциясы W1(s) қ осымша буынды қ осуғ а болады.
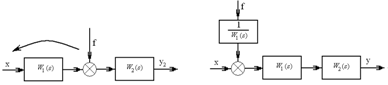
23 сурет – Сигнал бағ ытына қ арсы сумматорды ауыстыру
W1 (s) беріліс функциялы буынның кірісіне кіретін сыртқ ы ә серді f буынның шығ ысы мен кірісі арасына дә л сондай беріліс функциялы қ осымшабуындыорналастыра отырып, оның шығ ысына ауыстыруғ а болады.
Сигналдың таралу бағ ыты бойынша W1 (s) беріліс функциялы буынарқ ылы сумматорды ауыстыру кезінде байланыс тү зуінде сыртқ ы ә сер менсумматор арасына буынның беріліс функциялы қ осымша буынды қ осу керек(24 сурет).
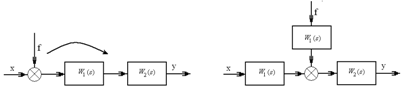
24 сурет – Сигнал бағ ыты бойынша сумматорды ауыстыру
4. Сумматор арқ ылы сумматорды ауыстыру қ осымша тү рлендірулерсіз- ақ жү зеге асырылады. Сигнал бойынша сумматор жә не тү йінді ауыстыруғ атү рлендірілген бө ліктің жанында қ осымша буын пайда болады –суммалаушынемесе салыстырушы.
24. Автоматты басқ ару жү йелерінің қ ұ рылымдық сұ лбаларының тағ айындалуы
Қ ұ рылымдық сұ лбалар жә не элементтерді қ осу
Басқ ару жү йлерінің математикалық моделінің сызбалық суреті АБТ-да қ ұ рылымдық сұ лба деп аталады. Қ ұ рылымдық сұ лбалардың элементтеріне тбуындар, тү йіндер, сумматор жә не салыстырмалы элементтер жатады. Буындар ішіне буынның беріліс функциясы жазылатын кіріс жә не шығ ыс шамалардың кө рсетулерімен тікбұ рышты тү рінде суреттеледі. Байланыс сызығ ындағ ы тармақ талу болатын нү ктелер тү йін деп аталады. Қ ұ рылымдық сұ лба элементтері 18- суретте кө рсетілген.

18 сурет – Қ ұ рылымдық сұ лбалардың элементтері
Сұ лба қ аншалық ты кү рделі болса да, онда ү ш типті байланыстар орын
алады:
- тізбектей;
- параллель;
- кері байланысты тізбектей.
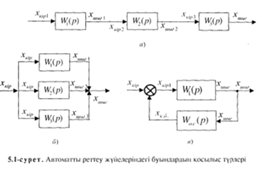
Буындарды тізбектей қ осу. Буындарды тізбектейқ осқ анда (5. 1, а-сурет) алдың ғ ы буынның шығ ыстық шамасы келесінің кірістік шамасы болады. Солсебептен тізбектей қ осылғ ан буындар жү йесінің берілісфункциясы жеке буындардың беріліс функцияларының кө бейтіндісіне тең: 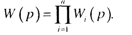
Буындарды параллель қ осу. Параллель қ осылғ анбуындардан тұ ратын жү йенің кірістік шамасы (5. 1, б-сурет) барлық буындардың кірісіне бір мезгілдеберіледі, ал оның шығ ыстық шамасы ә рбір жекебуындардың шығ ыстық шамаларының қ осындысына тең. Сондық тан параллель қ осылғ ан буындарданқ ұ ралғ ан жү йенің беріліс функциясы осы буындардың беріліс функцияларының қ осындысына тең: 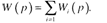
Буындарды қ арсы-параллель қ осу не кері байланысты қ осылыс. Қ арсы-параллель қ осылғ ан буындардың кірісіне жү йенің кірістік шамасымен бірғ е W2(p) кері байланыс буыны арқ ылы ө ткен оның шығ ыстық шамасы да беріледі.
Қ осылыстың беріліс функциясы тө мендегі ө рнекпенанық талады: 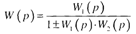
Бө ліміндегі «+» таң басы 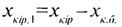 , болғ андағ ы теріс кері байланыста алынады.
, болғ андағ ы теріс кері байланыста алынады.
Ал « - » таң басы Хкір1=Хкір+Хкбболғ андағ ы оң кері байланыста алынады.
Реттеу жү йелерінде олардың жү мысының орнық тылығ ын қ амтамасыз ету ү шін ә детте теріс керібайланыс қ олданылады, ендеше 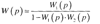
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|