
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ”
„ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ”
Тема: Невизначений інтеграл.
Означення. Функція F(х) називається первісною функції 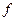 (х) на відрізку [a,b], якщо в усіх точках цього відрізка виконується рівність F¢(x) =
(х) на відрізку [a,b], якщо в усіх точках цього відрізка виконується рівність F¢(x) = 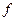 (x).
(x).
Якщо F(х) будь-яка первісна 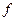 (х), то будь-яка інша первісна для
(х), то будь-яка інша первісна для 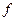 (х) має вигляд F(х) + С, де С – сonst.
(х) має вигляд F(х) + С, де С – сonst.
Означення. Сукупність усіх первісних функцій 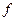 (х) називається невизначеним інтегралом функції
(х) називається невизначеним інтегралом функції 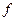 (х) і позначається
(х) і позначається
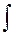
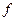 (х)dx = F(x) + C,
(х)dx = F(x) + C,
де F(x) – деяка первісна функції 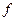 (х), а С – довільна стала.
(х), а С – довільна стала.
Символ 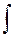 називається знаком інтеграла,
називається знаком інтеграла, 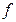 (х) – підінтегральна функція,
(х) – підінтегральна функція, 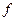 (х)dx – підінтегральний вираз, х – змінна інтегрування.
(х)dx – підінтегральний вираз, х – змінна інтегрування.
Операцію знаходження невизначеного інтеграла називають інтегруванням.
 Властивості невизначеного інтеграла:
Властивості невизначеного інтеграла:
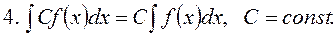
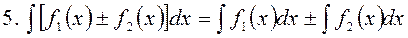
Таблиця основних інтегралів
1. 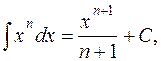
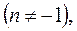
2. 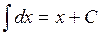 .
.
3. 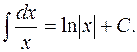
4. 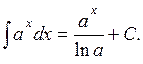
5. 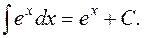
6. 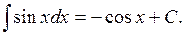
7. 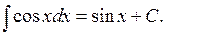
8. 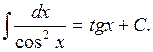
9. 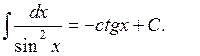
10. 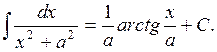
11. 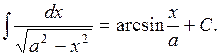
12. 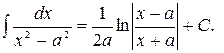
13. 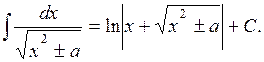
Основними методами інтегрування є безпосереднє інтегрування, заміна змінної або підстановка та інтегрування частинами.
Метод безпосереднього інтегрування ґрунтується на загальних властивостях невизначеного інтеграла, таблиці інтегралів і тотожних перетвореннях підінтегральної функції.
Приклад . Знайти інтеграл: 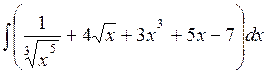 .
.
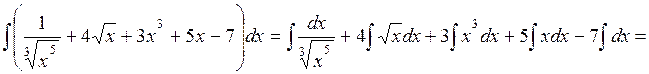
= 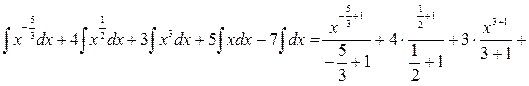
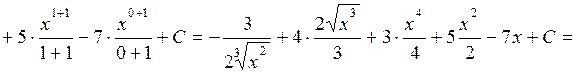
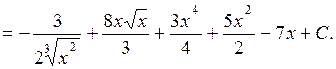
Метод заміни змінної або підстановки ґрунтується на введенні під знак інтеграла такої змінної, після підстановки якої та заміни диференціала заданої змінної на диференціал нової змінної, одержимо табличний інтеграл.
Приклад . Знайти інтеграл: 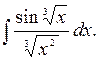
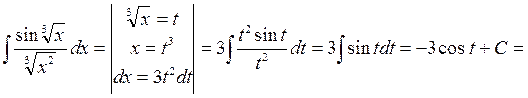
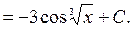 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|