
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Заняття №4
Заняття №4
Тема:Центр ваги. Геометричні характеристики плоских перерізів.
Мета:Сформувати у студентів поняття про центр ваги. Навчити визначати по-лярний та осьовий моменти інерції. Розвивати пізнавальні здібності студен-тів.
Тип заняття:Лекція з елементами контролю знань.
Тривалість заняття:2 год.
Хід заняття:
1. Організаційна частина.
2. Повідомлення теми, мети заняття.
3. Актуалізація опорних знань студентів:
3.1. Сформулюйте умови рівноваги системи пар.
3.2. Теорема Варіньона.
3.3. Сформулюйте умови рівноваги плоскої системи сил.
4. Вивчення нового теоретичного матеріалу:
4.1. Геометричні характеристики плоских перерізів.
4.2. Центр паралельних сил.
4.3. Центр ваги.
4.4. Координати центра ваги плоских фігур та прокатних профілів.
4.5. Статичний момент площини.
4.6. Полярний та осьовий момент інерції перерізів.
4.7. Момент опору перерізу.
5. Закріплення вивченого матеріалу:
5.1. Задача 1, 2 стор. 47.
5.2. Задача 2, 3 стор.5 3.
6. Підведення підсумків заняття.
7. Домашнє завдання:
7.1. Опрацювати §§ 23-27.
7.2. Задача 6, 7 стор. 53.
Короткі теоретичні відомості:
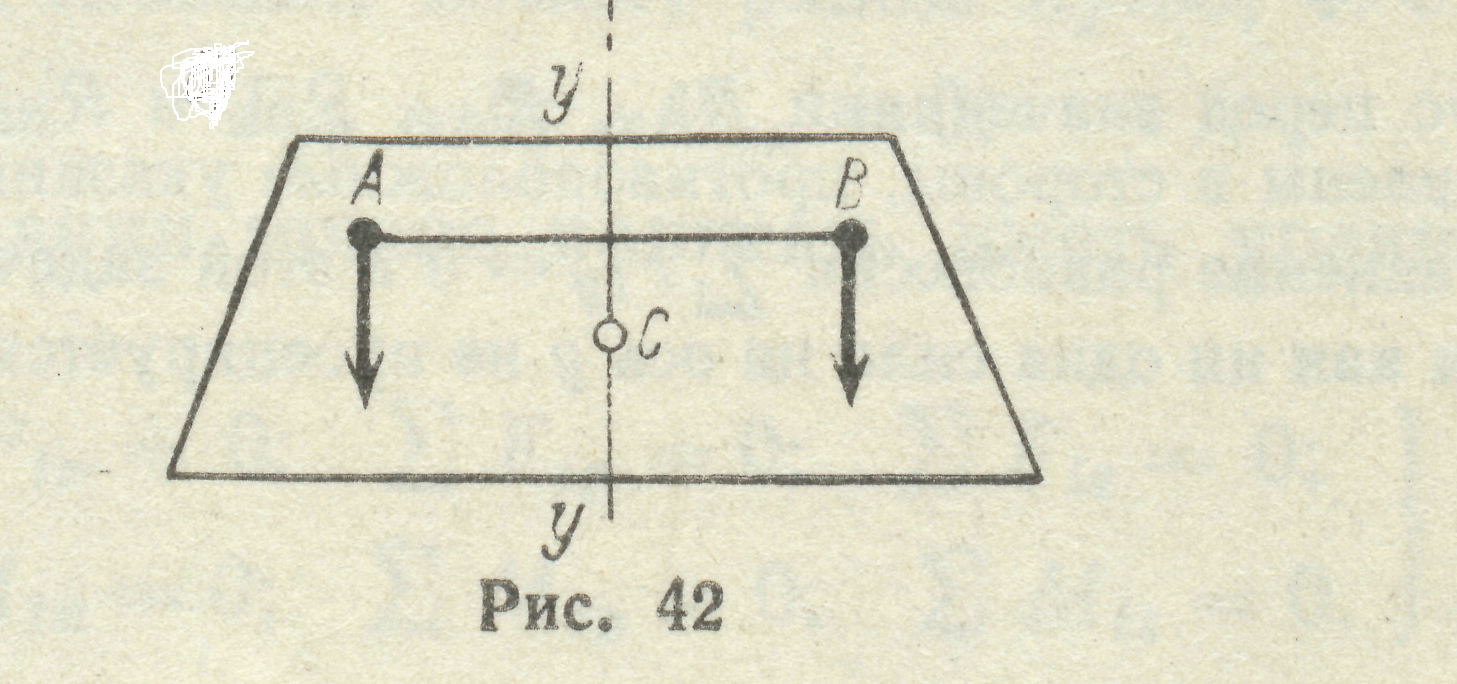 1.Якщо на тіло діють дві паралельні сили, то рівнодіюча цих сил дорівнює їх сумі, паралельна до них, напрямлена в ту ж сторону, а її лінія дії ділить плече на частини обернено пропорційні цим силам (рис. 13).
1.Якщо на тіло діють дві паралельні сили, то рівнодіюча цих сил дорівнює їх сумі, паралельна до них, напрямлена в ту ж сторону, а її лінія дії ділить плече на частини обернено пропорційні цим силам (рис. 13).
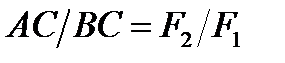 .
.
Точка С називається центром паралельних сил, її по-ложення не залежить від напрямку сил, які додаються. Будь-яке тло можна розглядати, як складене з великої кількості малих частинок, на які діють сили тяжіння.
Рис. 13 Рівнодіючу цих сил називають силою тяжіння.
2. Центр паралельних сил тяжіння, діючих на всі частинки тіла, називають цент-ром тяжіння тіла. Центр тяжіння тіла не змінює свого розташування при повороті тіла
3.Положення (координати) центра просторової системи паралельних сил визнача-ють за формулами:
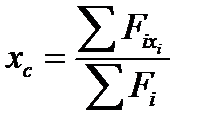 ;
; 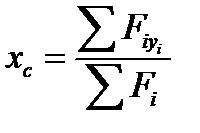 ;
; 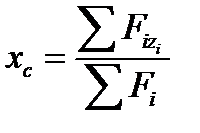 .
.
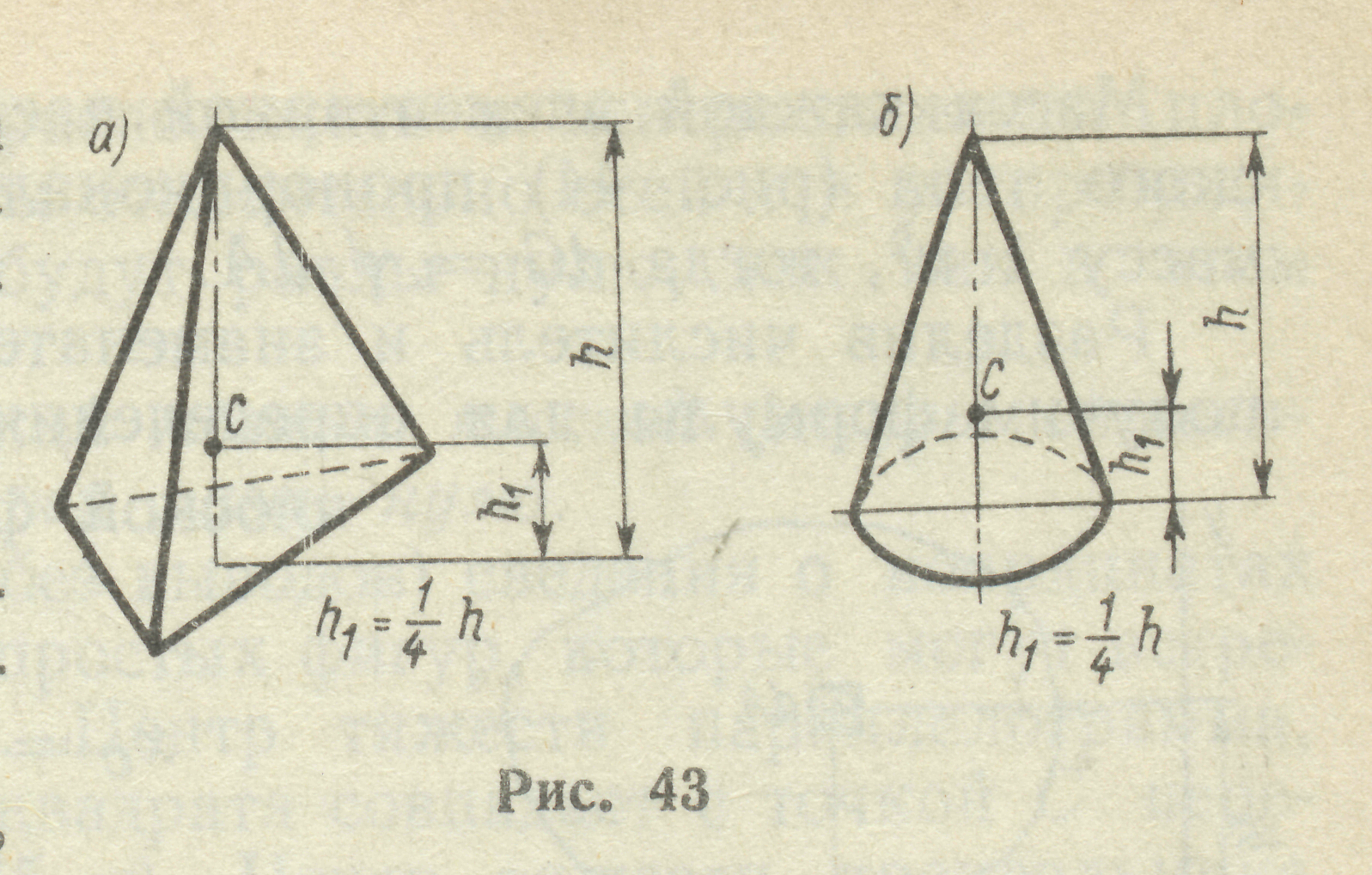 4.Центр ваги симетричного тіла завжди лежить в площі симетрії. Площа симетрії поділяє тіло таким чином, що кожній матеріальній точці, яка знаходиться по одну сторону площини, відповідає однакова за масою точка по іншу сторону площини, причому лінія, яка з’єднує ці точки, перпендикулярна до площини симетрії та ділиться нею пополам. Центр ваги плоскої симетричної фігури лежить на вісі симетрії (рис. 14).
4.Центр ваги симетричного тіла завжди лежить в площі симетрії. Площа симетрії поділяє тіло таким чином, що кожній матеріальній точці, яка знаходиться по одну сторону площини, відповідає однакова за масою точка по іншу сторону площини, причому лінія, яка з’єднує ці точки, перпендикулярна до площини симетрії та ділиться нею пополам. Центр ваги плоскої симетричної фігури лежить на вісі симетрії (рис. 14).
Для плоских тіл центр тяжіння визначають Рис. 14 тільки двома координатами, а об’ємних - трьома:
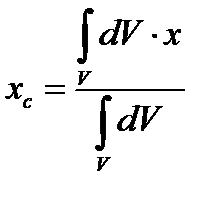 ;
; 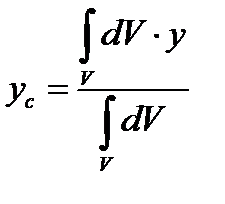 ;
; 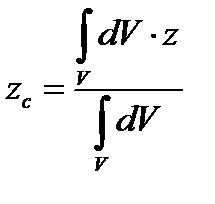 ;
;
де, 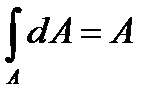 - повна площа фігури.
- повна площа фігури.
5. Для визначення центра тяжіння плоского тіла складної форми, тіло ділять на елементарні площі. Маса однорідного тіла пропорційна його елементарній площі.
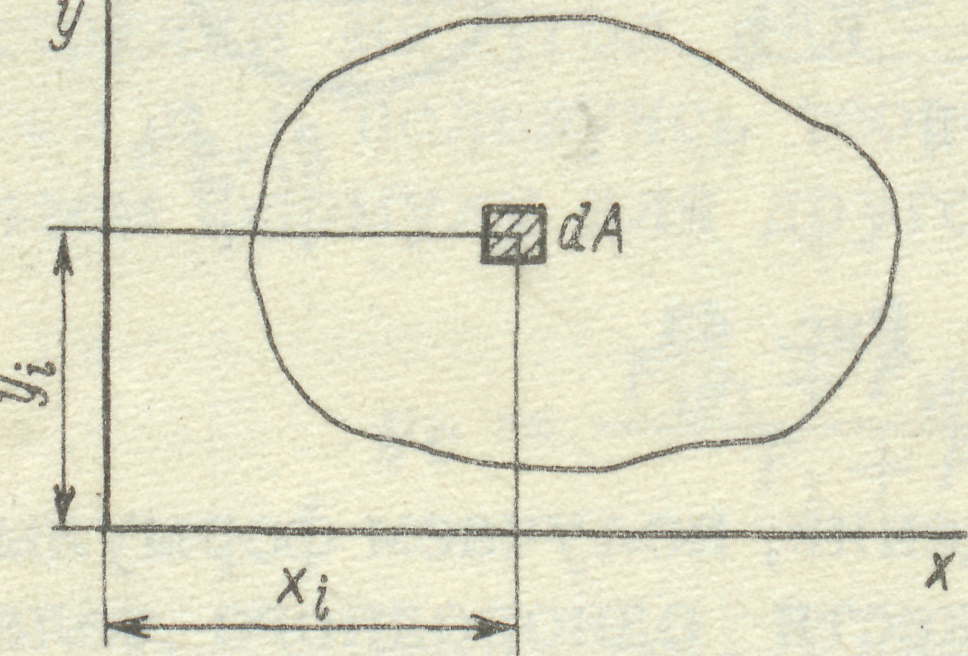 Добуток елементарної площі фігури на відстань від її центра ваги до будь-якої вісі називається статичним моментом ваги (рис.15).
Добуток елементарної площі фігури на відстань від її центра ваги до будь-якої вісі називається статичним моментом ваги (рис.15).
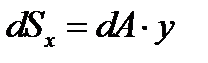 ;
;
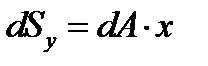 .
.
Сума статичних моментів всіх частин фігури називається статичним моментом площі фігури відносно даної вісі.
Рис. 15 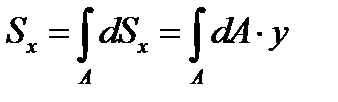 ;
;
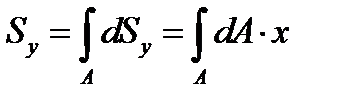 .
.
Статичний момент площі визначається одиницями довжини в третьому ступені ( 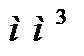 ,
, 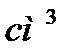 ,
, 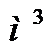 ).
).
Якщо початок координат розмістити в центрі тяжіння площини, то статичні мо-менти відносно осей 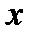 та
та 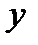 , які проходять через центр тяжіння, будуть дорівнювати нулю. Відповідно статичний момент плоскої фігури відносно будь-якої центральної вісі дорівнює нулю.
, які проходять через центр тяжіння, будуть дорівнювати нулю. Відповідно статичний момент плоскої фігури відносно будь-якої центральної вісі дорівнює нулю.
6.Полярним моментом інерції перерізу називається взята по всьому перерізу сума добутків або інтеграл елементарних площ на квадрати їх відстаней від деякої точки О до перерізу (рис. 16а).
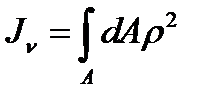 .
.
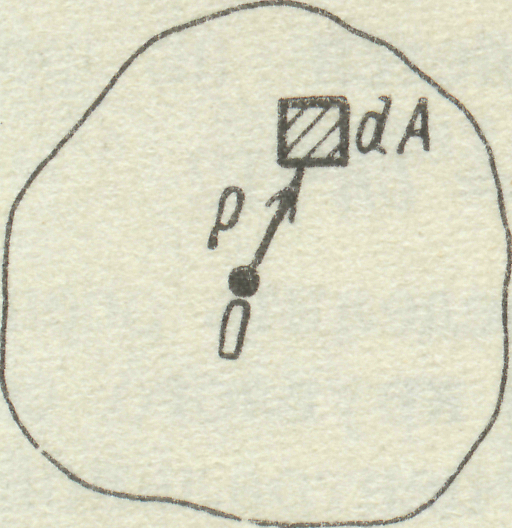
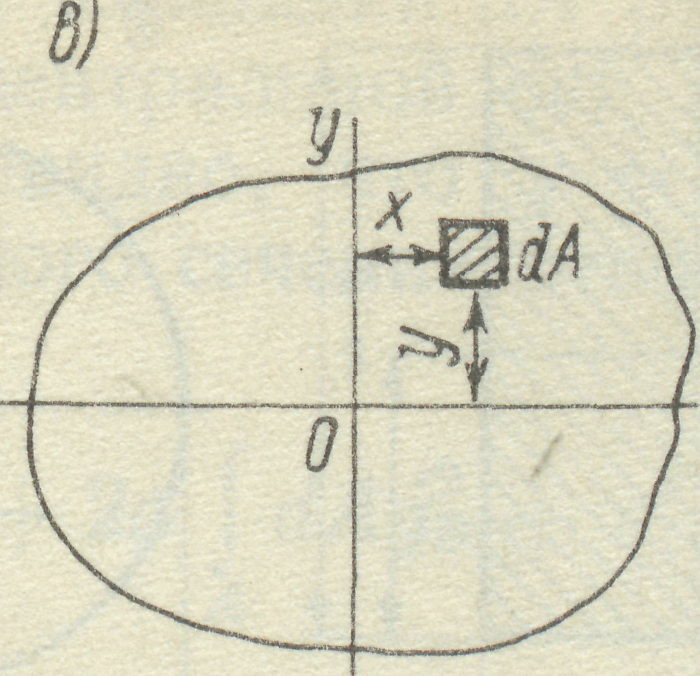
а б
Рис. 16
Осьовим моментом інерції перерізу називається взята по всьому перерізу сума добутків або інтеграл елементарних площ на квадрати їх відстаней до деякої вісі, яка лежить в площині перерізу, який розглядається (рис. 16б).
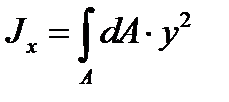 ;
;
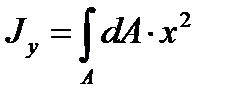 .
.
Значення осьового моменту служить характеристикою здатності балки опиратись згину.
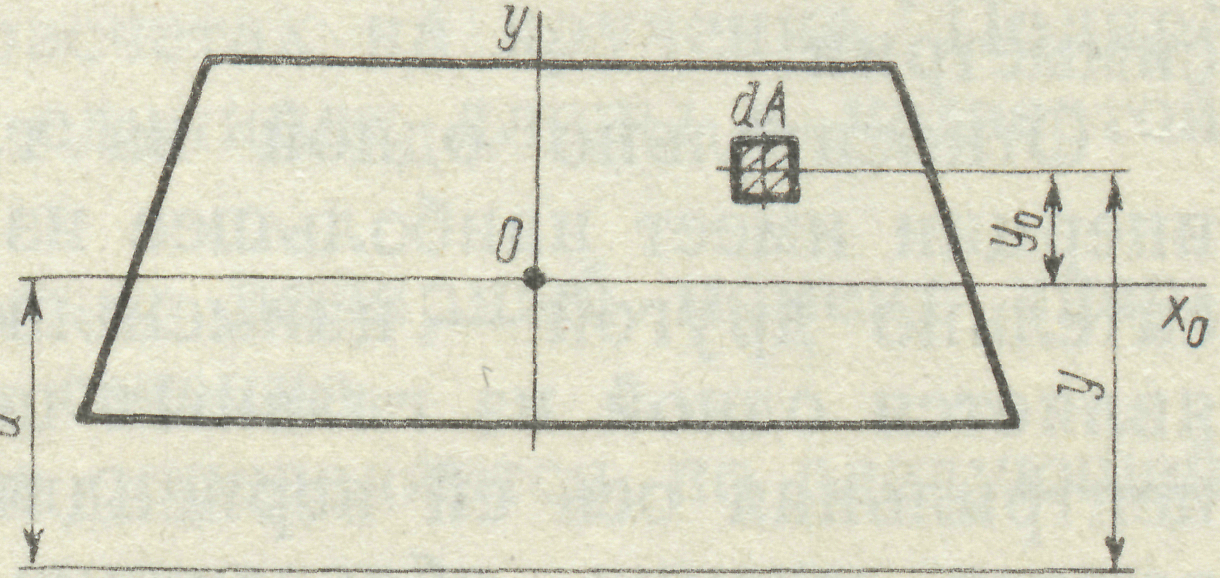 7. Для обчислення осьових моментів інерції складних перерізів користуються тео-ремою про моменти інерції відносно паралельних осей. Момент інерції перерізу відносно вісі, яка не проходить через його центр ваги, дорівнює сумі моментів інерції перерізу відносно його централь-ної вісі, яка паралельна даній вісі, та добутку площі перерізу на квадрат відстані між осями (рис. 17).
7. Для обчислення осьових моментів інерції складних перерізів користуються тео-ремою про моменти інерції відносно паралельних осей. Момент інерції перерізу відносно вісі, яка не проходить через його центр ваги, дорівнює сумі моментів інерції перерізу відносно його централь-ної вісі, яка паралельна даній вісі, та добутку площі перерізу на квадрат відстані між осями (рис. 17).
Рис. 17 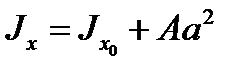 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|