Заняття №2

Заняття №2

Тема:Плоска система збіжних сил.

Мета:Сформувати у студентів поняття про плоску систему збіжних сил; навчити будувати силовий багатокутник, розв`язувати задачі на рівновагу плоскої системи збіжних сил; розвивати пізнавальні здібності студентів.

Тип заняття:Лекція з елементами контролю знань.

Тривалість заняття:2 год.

Хід заняття:

1. Організаційна частина.

2. Повідомлення теми, мети заняття.

3. Актуалізація опорних знань студентів:

3.1. Що називається абсолютно твердим тілом?

3.2. Що називається системою сил?

3.3. Сформулюйте аксіоми статики.

4. Вивчення нового теоретичного матеріалу:

4.1. Система збіжних сил.

4.2. Визначення рівнодіючої плоскої системи збіжних сил.

4.3. Силовий багатокутник.

4.4. Проекція сили на вісь.

4.5. Рівняння рівноваги плоскої системи збіжних сил.

5. Закріплення вивченого матеріалу.

5.1. Вправа 4 (стор. 17).

5.2. Вправа 5 (стор. 20).

6. Підведення підсумків заняття.

7. Домашнє завдання:

7.1. Опрацювати главу2 (стор. 12-21).

7.2. Задача 2 (стор. 21).

Короткі теоретичні відомості:

1.Сили називають збіжними, якщо їх лінії дії перетинаються в одній точці. Розріз-няють плоску та просторову систему збіжних сил.

2. За третьою аксіомою статики силу можна перенести вздовж лінії її дії, тому збіжні сили можна завжди перенести в одну точку та побудувати силовий багато-кутник (рис. 5).

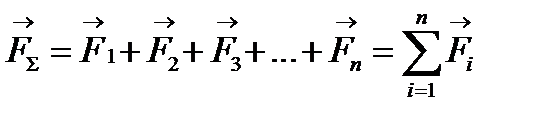
Рис. 5

Якщо при побудові силового багатокутника кінець останньої сили співпаде з по-чатком першої, то рівнодіюча системи дорівнює нулю. Така система збіжних сил знаходиться в стані рівноваги.

3.Віссю називають пряму лінію, для якої визначено відповідний напрям.

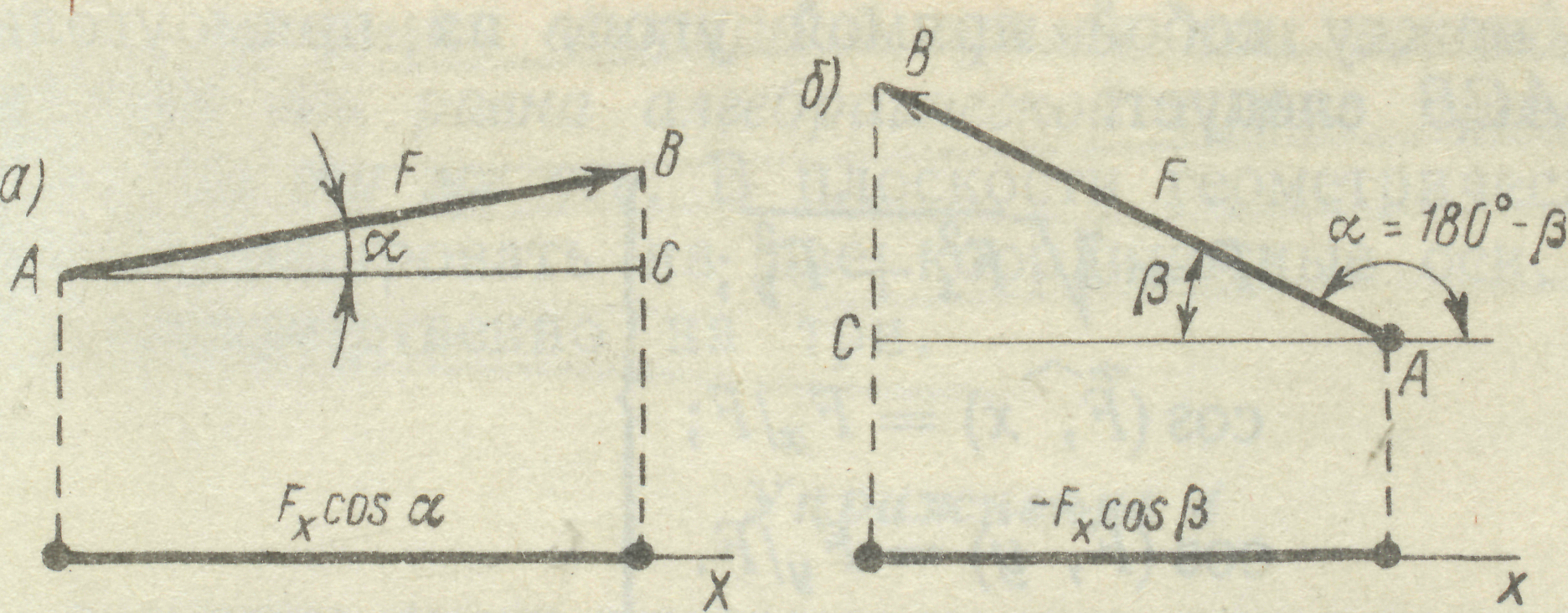Проекція вектора на вісь є скалярною величиною, яка обмежена відрізком вісі утвореним перпендикулярами, опу-щеними на неї з кінців вектора.

Проекція вважається додатною, якщо напрямок від початку проекції до її кінця співпадає з позитивним напрямком вісі. Проекція вважається від`ємною, якщо напрямок від почат-ку проекції до її кінця протилежний Рис. 6 додатному напрямку вісі.

3.1. У випадку, коли вектор сили 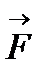становить з додатним напрямом вісі 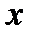гострий кут 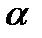(рис. 6 а), щоб знайти проекцію необхідно з початку та кінця вектора сили опустити перпендикуляри на вісь 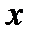; отримаємо:

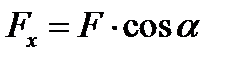Проекція в даному випадку додатна.

3.2. Якщо сила 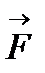складає з позитивним напрямом вісі 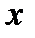тупий кут 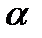(рис.6 б), то 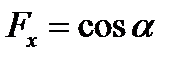, але оскільки ;

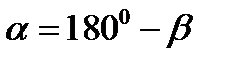отримаємо:

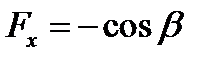Проекція в даному випадку від’ємна.

3.3. У випадку, коли сила 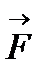перпендикулярна до осі 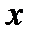, проекція сили 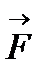на вісь 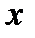дорівнює нулю:

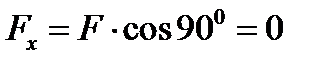Проекція сили на вісь координат дорівнює добутку модуля сили на косинус кута між вектором сили та позитивним напрямком вісі/

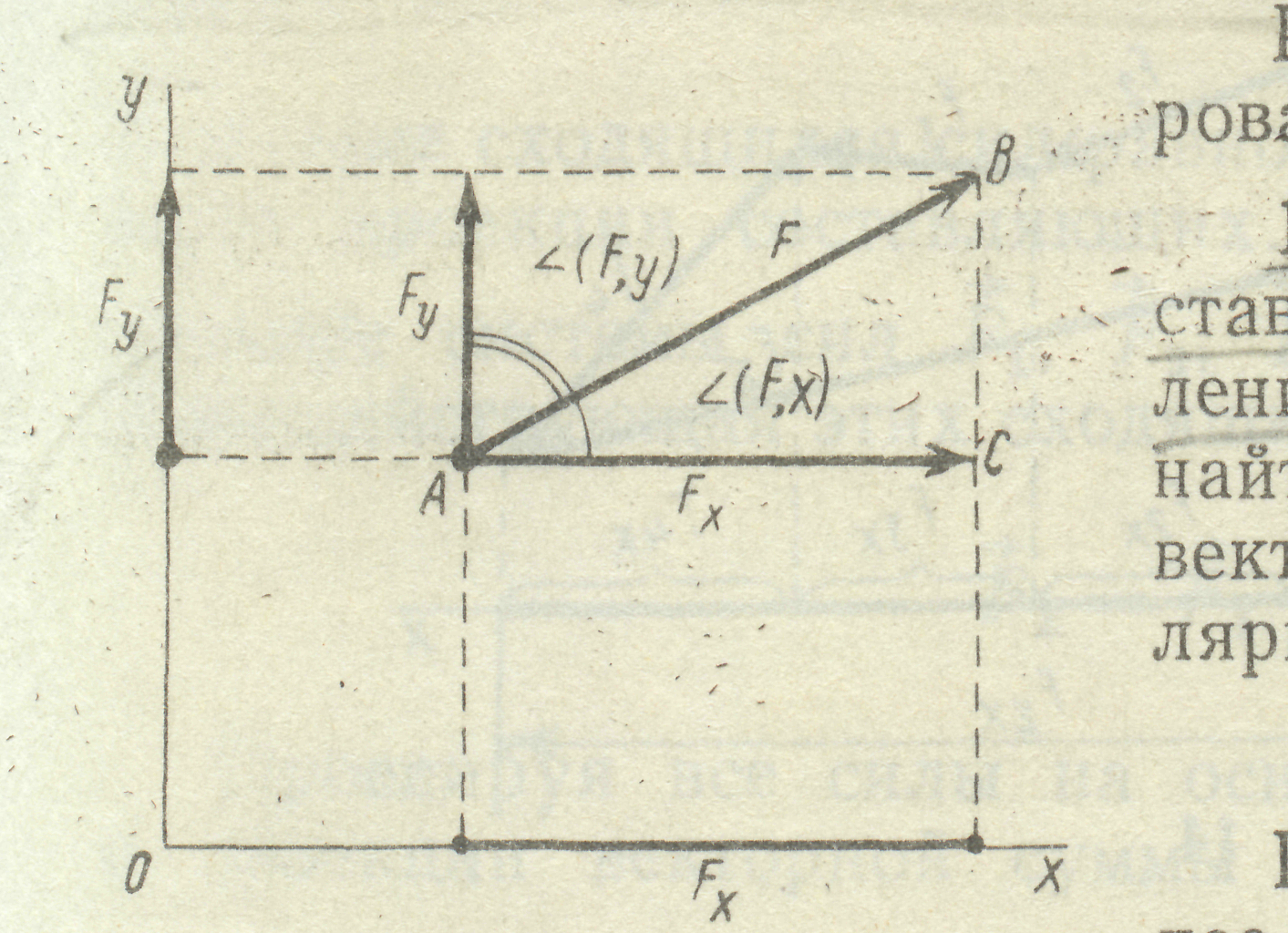4.Силу, розміщену на площині 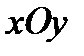можна спроектувати на дві координатні вісі 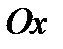та 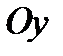(рис.7). Оскільки проекції утворюють між собою прямий кут, з прямокутного трикутника АВС маємо:

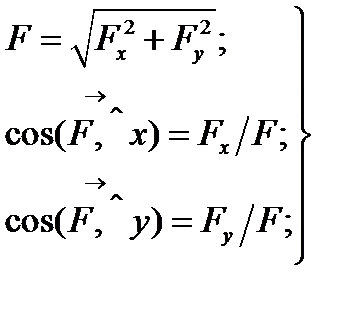
Даними формулами користуються для визначе-ння модуля та напрямку сили, якщо відомі її про-

Рис. 7 екції на вісі координат.

5. Проекція векторної суми або рівнодіючої на будь-яку вісь дорівнює алгебраїч-ній сумі проекцій векторів, які додаються, на ту саму вісь (рис. 8).

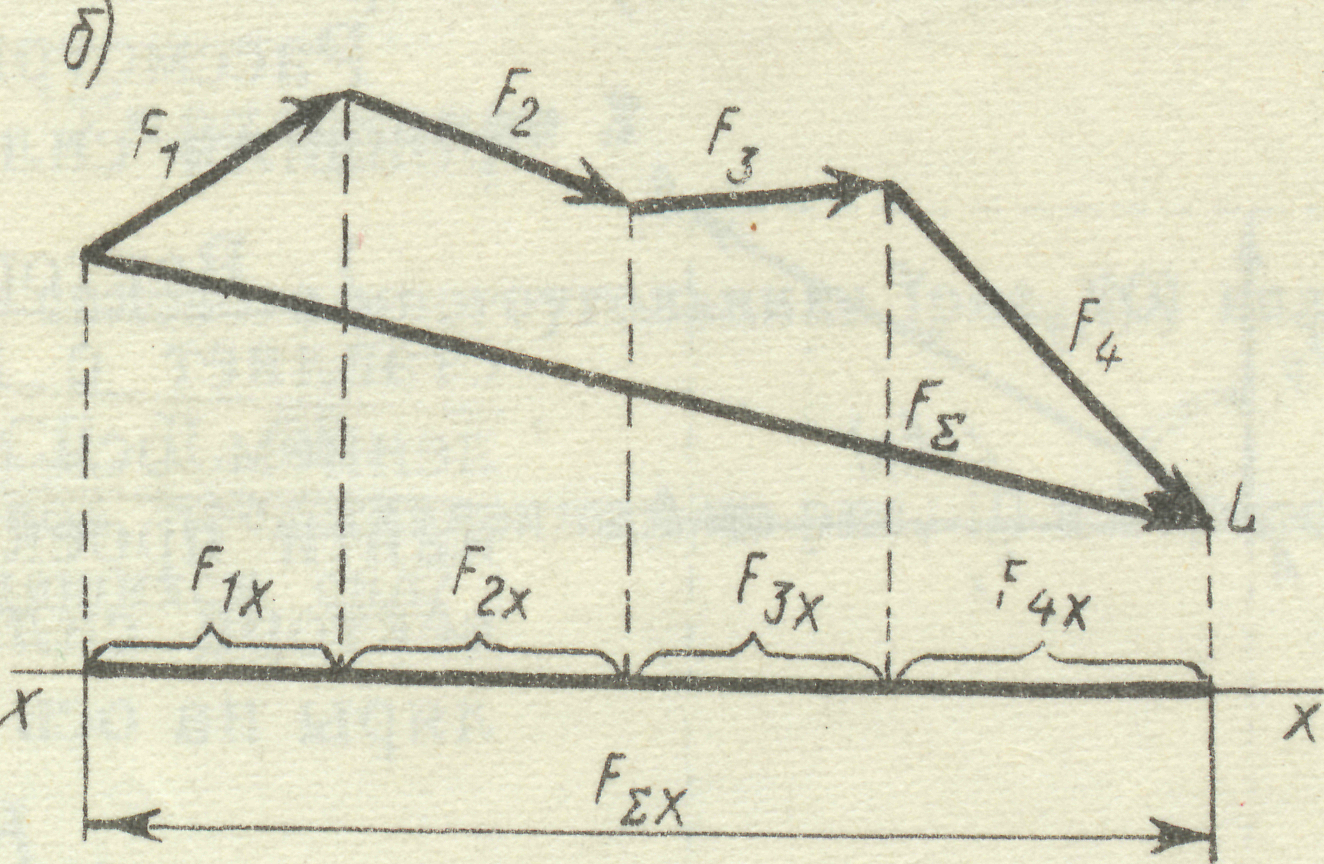
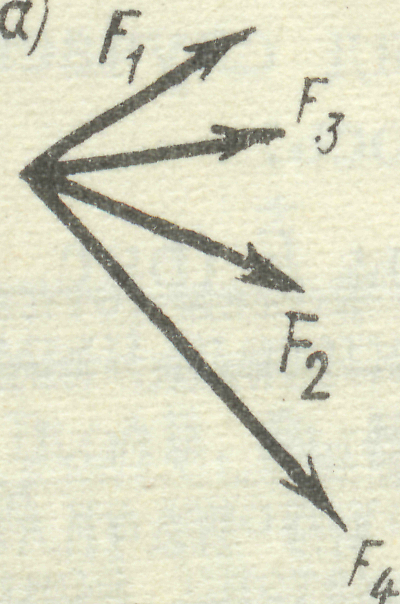
Рис. 8

5.Система збіжних сил знаходиться в стані рівноваги, якщо алгебраїчна сума проекцій її доданків на кожну з двох координатних осей дорівнюють нулю.

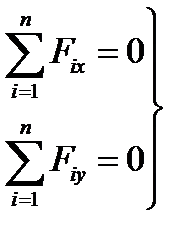Рівняння рівноваги плоскої системи збіжних сил.

Для спрощення запису рівнянь можна опускати індекси та суми.

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒