Заняття №3

Заняття №3

Тема:Довільно плоска система сил.

Мета:Сформувати у студентів поняття про довільно плоску систему сил, вивчити теорему Варіньона, навчити розв`язувати задачі на рівновагу плоскої системи сил.

Тип заняття:Лекція з елементами контролю знань.

Тривалість заняття:2 год.

Хід заняття:

1. Організаційна частина.

2. Повідомлення теми, мети заняття.

3. Актуалізація опорних знань студентів:

3.1. Умови рівноваги плоскої системи.

3.2. Що називається моментом сили?

3.3. Що називається центром моменту, плечем моменту.

4. Вивчення нового теоретичного матеріалу:

4.1. Момент сили.

4.2. Паралельний перенос сили.

4.3. Приведення плоскої системи сил до центру зведення.

4.4. Головний вектор і головний момент системи.

4.5. Теорема Варіньона.

4.6. Рівняння рівноваги.

4.7. Балочні системи, види навантажень, та визначення напрямів опорних реак-цій балок.

5. Закріплення вивченого матеріалу.

5.1. Вправа 10 (стор. 32).

5.2. Вправа 11 (стор. 39).

6. Підведення підсумків заняття.

7. Домашнє завдання:

7.1. Опрацювати §§16-22.

7.2 Задача 9 (стор. 40).

Короткі теоретичні відомості:

1 Момент сили 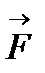відносно точки О визначається добутком модуля сили на дов-жину перпендикуляра, опущеного з точки на лінію дії сили.

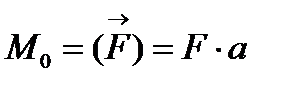
При закріпленні тіла в точці О сила 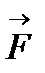намагається повернути тіло навколо цієї точки. Точка О, відносно якої береться момент, називається центром моменту, а довжина перпендикуляра 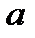- плечем моменту.

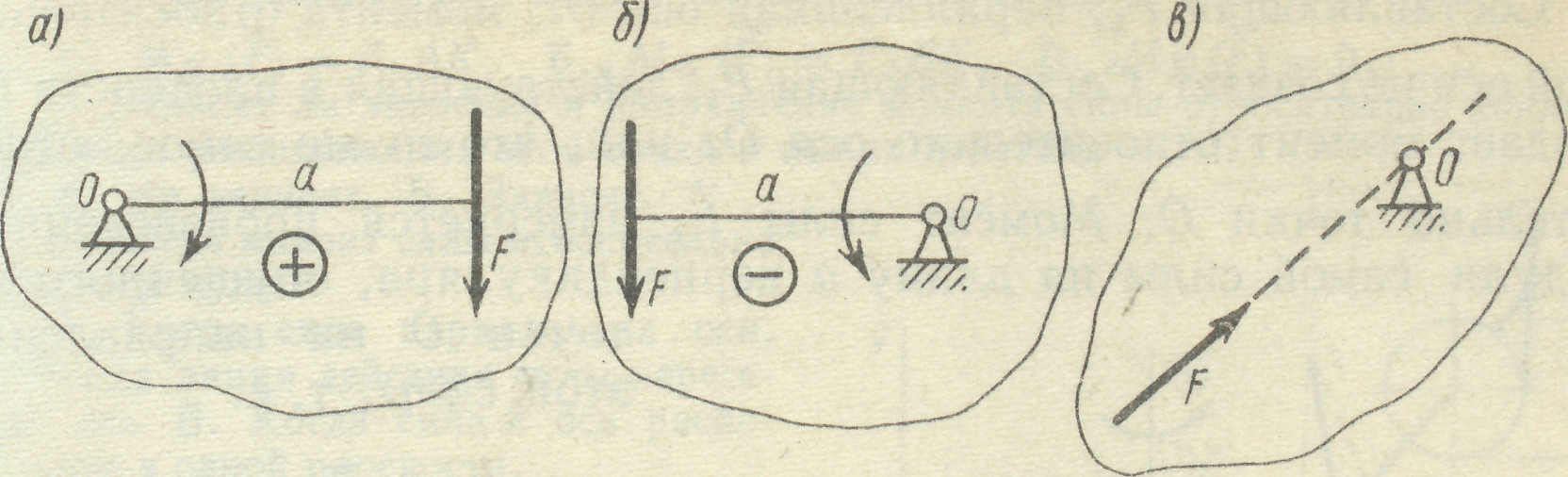
Рис 9

Момент прийнято вважати додатним, якщо сила намагається обертати тіло за годинниковою стрілкою (рис. 9а), а від’ємним, якщо проти годинникової стрілки (рис. 9 б). У випадку коли лінія дії сили проходить через дану точку, момент сили дорівнює нулю (рис. 9в).

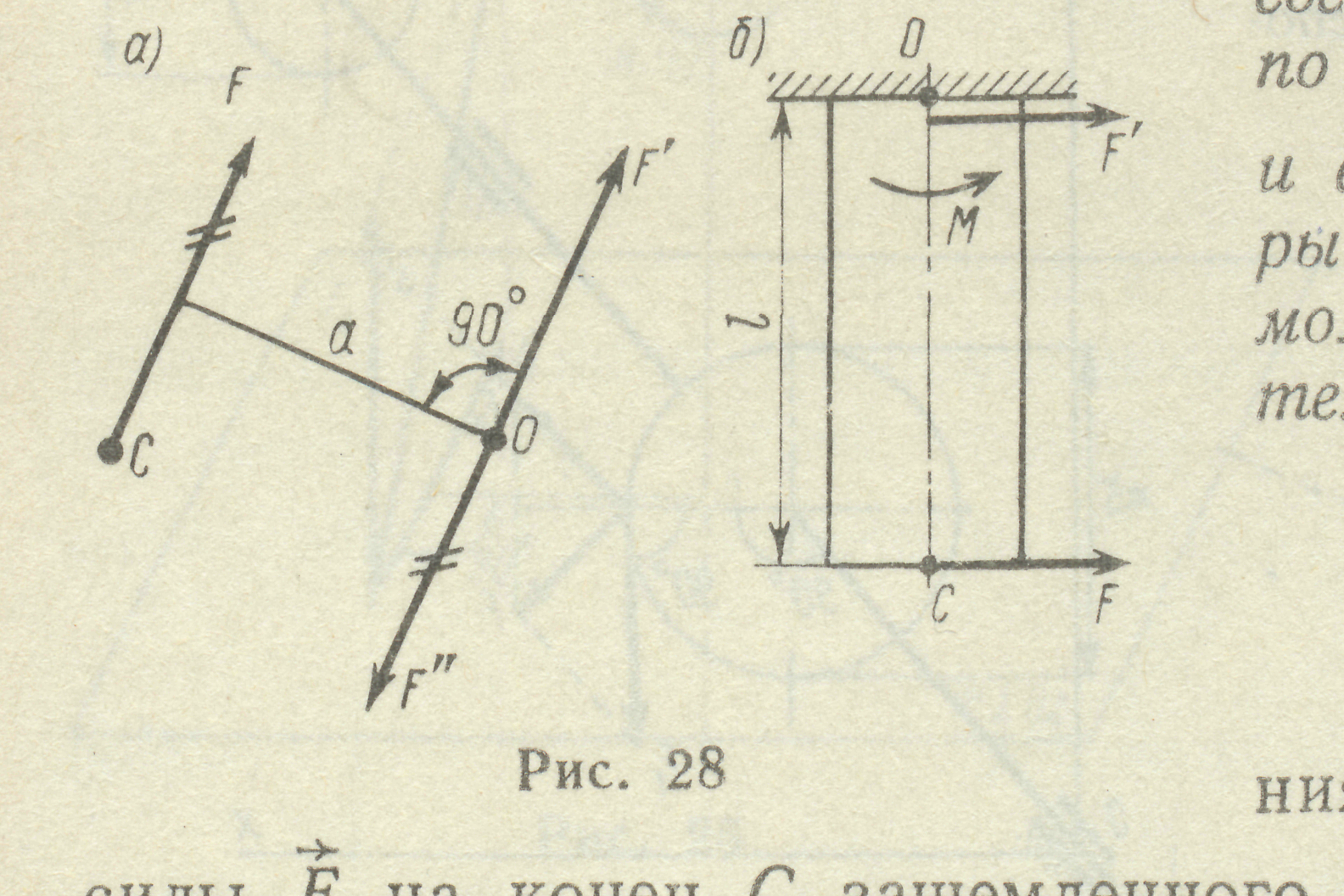2. При приведенні сили 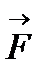до довільної точки, яка не ле-жить на лінії дії сили, отримується еквівалентна система, яка складається з сили, такої самої за модулем та напрям-ком, як і сила 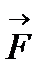, та приєднаної пари сил, момент якої дорівнює моменту даної сили відносно точки приведення (рис. 10):

Рис. 10 .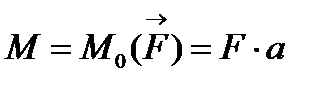

3. Плоска система сил в результаті приведення до даної точки О (рис. 11) заміню-ється еквівалентною їй системою, яка складається з однієї сили (головного вектора) та однієї пари (головного моменту).

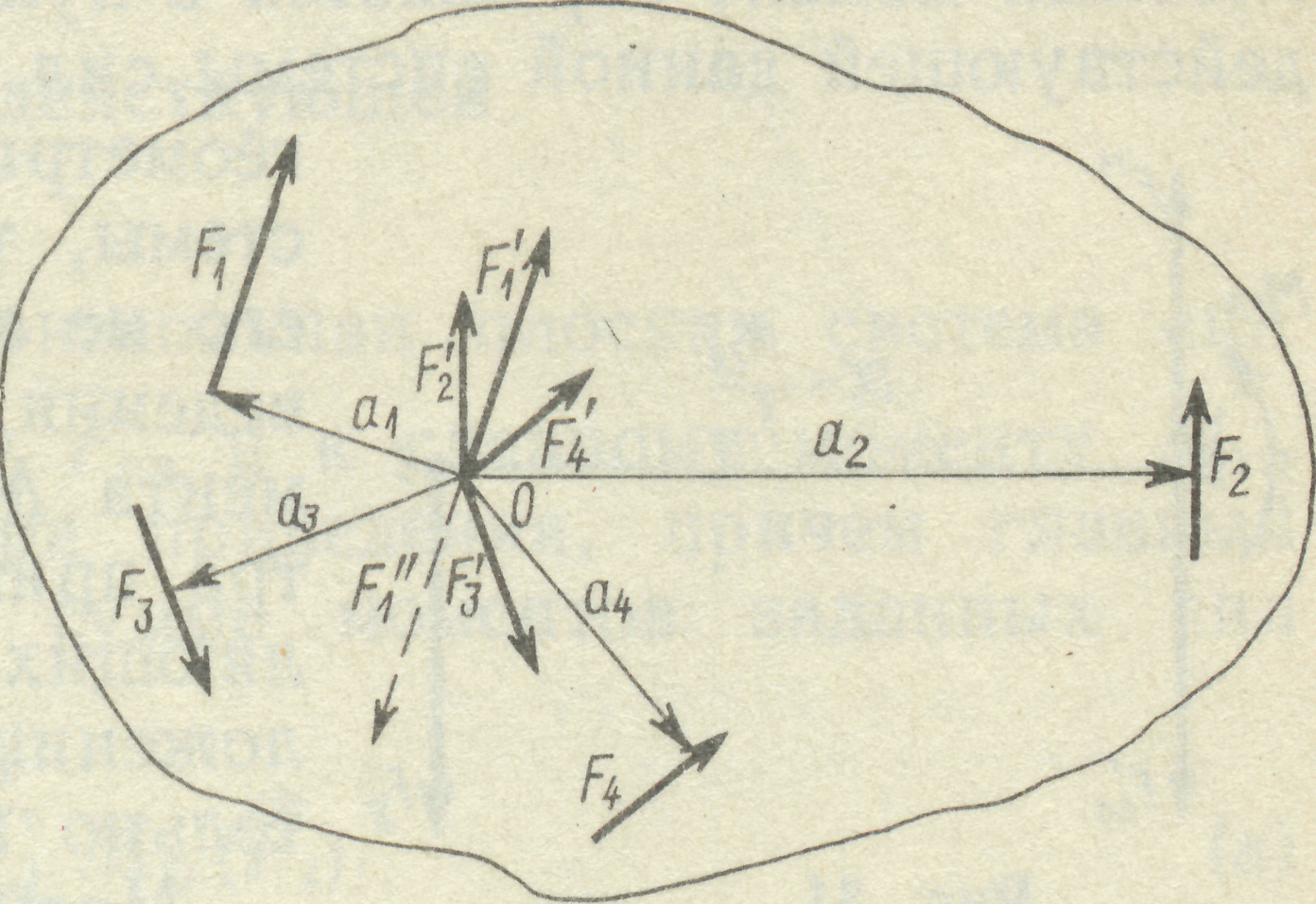
Рис. 11

; ;

; .

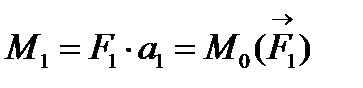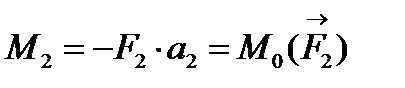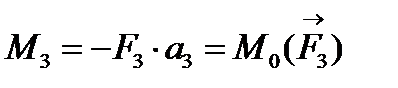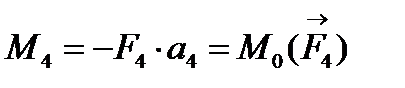4. Сили, що збігаються в точці О можна замінити однією силою 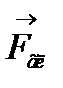, яка дорівнює геометричній сумі складових:

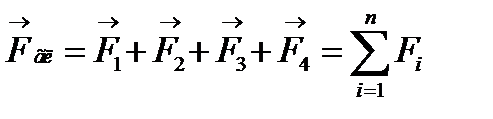Силу , яка дорівнює геометричній сумі заданих сил, називають головним вектором системи.

Момент, який дорівнює алгебраїчній сумі моментів заданих сил відносно точки О називається головним моментом:

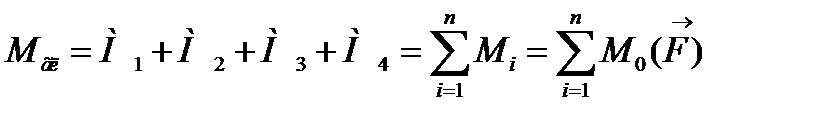
5. Теорема Варіньона: Момент рівнодіючої плоскої системи сил відносно довільно взятої точки дорівнює алгебраїчній сумі моментів складових сил відносно тієї ж точки:

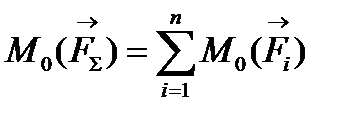6. Для рівноваги системи сил, довільно розміщених на площині, необхідно і доста-тньо, щоб головний вектор та головний момент цих сил відносно будь-якого центра кожний дорівнював нулю:

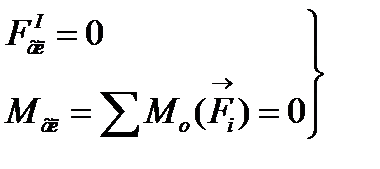
7. Балки (балочні системи) тіла видовженої форми призначені для сприйняття поперечних навантажень.

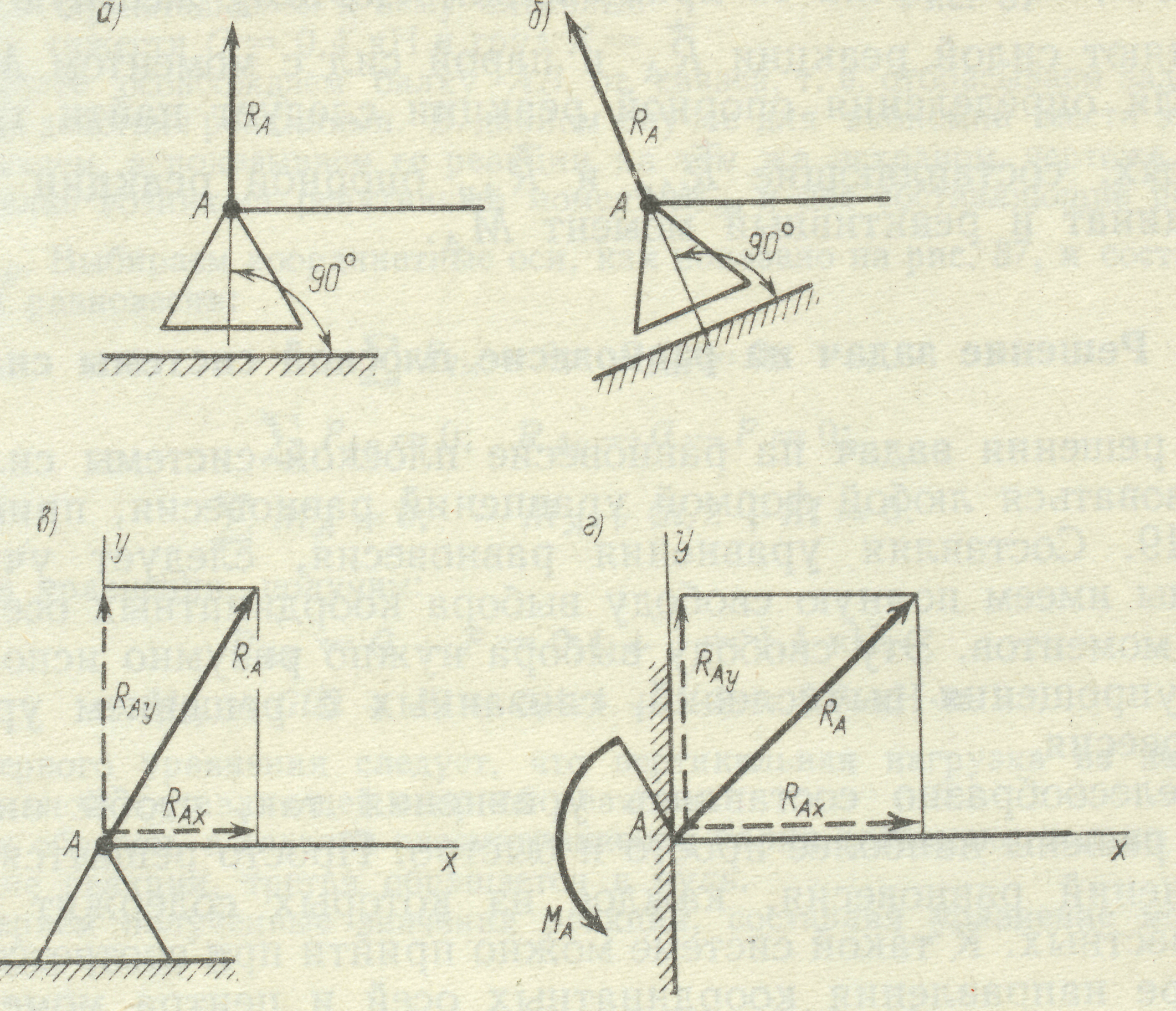
Рис. 12

Шарнірно-рухома опора (рис. 12а, б) (допускає поворот навколо вісі шарніра та лінійне переміщення паралельно опорної площини).

Шарнірно нерухома опора (рис. 12в) (допускає поворот тільки навколо вісі шарніра).

Жорстке защемлення (рис. 12г) (не допускає ніяких лінійних переміщень та поворотів).

Для рішення задач на рівновагу плоскої системи сил можна користуватись будь-якою формулою рівноваги. В якості моментів рекомендують вибирати точку, де перетинаються дві невідомі сили; рівняння моментів відносно цієї точки матиме одне невідоме. Напрямок координатних осей 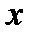та 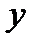необхідно вибирати таким чином, щоб вісі були перпендикулярні деяким невідомим силам (при складанні рів-нянь проекцій невідомі, перпендикулярні відповідній вісі, в ці рівняння не ввійдуть.

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒