Лекция 17

Агрегатные состояния вещества. Условия равновесия фаз: отношение масс вещества, находящемся в равновесном двухфазном состоянии. Анализ равновесного двухфазного состояния вещества с помощью термодинамического потенциала Гиббса. Фазовые переходы первого рода в двухфазной термодинамической системе: уравнение Клапейрона - Клаузиуса. Диаграммы состояний при фазовых переходах в термодинамической системе. Фазовые переходы второго рода в двухфазной термодинамической системе. Критические явления при фазовых переходах в термодинамической системе. Отличительные черты кристаллического состояния твёрдых тел. Классификация кристаллов твёрдых тел. Физические типы кристаллических решёток твёрдых тел. Дефекты в кристаллах твёрдых тел. Теплоёмкость кристаллов твёрдых тел.

Основные представления о строении жидкостей. Поверхностное натяжение и свободная поверхностная энергия. Равновесие смачивающей и несмачивающей капель жидкости на поверхности твердого тела. Капиллярный эффект. Формула Лапласа для поверхностного натяжения, дополнительное давление, создаваемое сферической поверхностью жидкости. Анализ равновесного состояния границы раздела между фазами вещества с помощью термодинамического потенциала Гельмгольца. Анализ равновесного состояния границы раздела жидкость - газ с помощью термодинамического потенциала Гельмгольца. Применение термодинамического потенциала Гельмгольца для определения температурной зависимости коэффициента поверхностного натяжения жидкости

Агрегатные состояния вещества. Условие равновесия фаз: отношение масс вещества, находящемся в равновесном двухфазном состоянии

Термодинамическийметод применим для описания не только однородныхпо физику - химическому составу сред, но и систем, состоящих из нескольких пространственно разнесённых частей, между которыми существует граница раздела. Проще всего описывать термодинамические системы, у которых составные части находятся в равновесныхсостояниях, а через границы раздела не происходит перенос вещества, энергии и импульса. Такая термодинамическая система является равновесной и для неё применимы методы равновесной термодинамики.

Если составные части термодинамической системы не находятся между собой в равновесии, то возникают термодинамическиепотоки через границы их раздела. Считая происходящие в системе процессы квазистатическими, а потоки малыми, можно использовать методы равновесной термодинамики и для неравновесной системы.

При описании пространственно неоднородныхсред применимо разбиение их на некоторое число однородныхпо своему составу частей, разделённых границами раздела. Макроскопическая часть среды, т.е. вещества, имеющая однородный физико - химический состав, называется фазой. Далее рассматриваются термодинамические системы, для описания состояния фаз которых применимы методы равновесной термодинамики.

Если среда однородна по всему своему объёму, то такая термодинамическая система будет однофазной, а если система состоит из двухили болееграничащих между собой однородных сред, то это двухфазнаяили многофазная термодинамическая система. Примером двухфазнойсистемы может служить стеклянный сосуд с налитой в него водой. В этом случае в системе имеются жидкаяи твёрдая фазы, которыми являются соответственно вода и стекло. Если в состав системы включить окружающий сосуд воздух, то она станет трёхфазнойсистемой. Смесь газов является однофазной системой, т.к. в этой смеси нет границы раздела.

Для равновесия фазнеобходимо, чтобы между ними наблюдалось тепловоеи механическоеравновесие. Первое из этих условий означает равенство T₁ и T₂ температур с разных сторон границы раздела фаз, т.е. T₁ = T₂ = T. Второе условие не обязательно соответствует равенству(4.1) из раздела

4. 1 "Физическая термодинамика" P₁ и P₂давлений с разных сторон границы раздела, т.к. сама граница, если она не является плоской, может создавать дополнительное межфазноедавление.Поэтому в общемслучае условие механическогоравновесия имеет следующий вид:

P₂= P₁+ ΔP₁₂, (4. 413)

где ΔP₁₂- дополнительное давление на первуюфазу, создаваемое границей её раздела со второй. Если считать границуфаз плоской, то(4.413) условие будет эквивалентнопредположению о равенстве давлений по обе стороны от неё, т.е. P₁= P₂= P.

При фазовыхпревращениях процессына границе раздела носят согласно параграфу "Статистическое обоснование второго начала термодинамики: формула Больцмана для статистической энтропии" из раздела 4.2 "Физическая термодинамика" статистическийхарактер.

На (рис.44)границе раздела водаи пар, происходит постоянный процесс перехода молекул из водыв пар и обратно. В равновесномсостоянии они взаимно компенсируются. Изотермическое при T температуре сжатие водяногопара, что сопровождается отводом Q_п теплоты, приводит при V = V_п объёме к образованию в Цл цилиндре под Пр поршнем, к которому приложен вектор F₁ внешней силы, насыщенного пара воды mмассой с P_н _п давлением. В состоянии, когда F модуль вектора F внешней силы достиг F₂значения, что сопровождается отводом Q_п, Q_в теплоты, часть насыщенного пара водыпревращается в воду m_в массой, которая занимает V_в' объём, а оставшаяся часть насыщенного пара водыm_п массой с P_н _п давлением занимает V_п' объём. В состоянии, когда F модуль вектора F внешней силы достигает F₃значения, весь насыщенный парпревращается в воду m массой, которая занимает V_в объём. Двухфазному равновесному состоянию вода + пар соответствует горизонтальный участок изотермы.

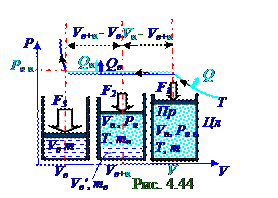
Удельные(4.2) из раздела 4.1 "Физическая термодинамика"объемыv_0п, v_0всоответственно насыщенного параи водыимеют следующий вид: v_0п = V_п/m; v_0в= V_в/m, (4.414) где (рис. 4.44) V_п - объёмнасыщенного пара воды, когда весьпарm массой в Цл цилиндре под Пр поршнем при значении F модуля вектора F внешней силы, равном F₁, превратился из ненасыщенногов насыщенноесостояние; V_в- объёмводы m массой, образовавшейся из всего насыщенного парав Цл цилиндре под Пр поршнем при

значении F модуля вектора F внешней силы, равном F₃.

При значении F модуля вектора F внешней силы, равном F₂, под Пр поршнем в Цл цилиндре при P_н _п давлении насыщенного пара водыm_в масса водыимеет с учётом (4.414) следующее значение: m_в= V_в'/v_0в ↔ V_в' = m_вv_0в↔ V_в' = m_вV_в/m, (4.415) где V_в'- объёмводыm_в массой, образовавшейся из насыщенного парав Цл цилиндре под Пр поршнем при значении F модуля вектора F внешней силы, равном F₂.

При значении F модуля вектора F внешней силы, равном F₂, под Пр поршнем в Цл цилиндре

m_п масса насыщенного пара воды при P_н _п давленииимеет с учётом (4. 414) следующее значение: m_п= V_п'/v_0п ↔ V_п' = m_пv_0п↔ V_п' = m_пV_п/m, (4.416) где V_п'- объёмнасыщенного пара водыm_п массойв Цл цилиндре под Пр поршнем при значении

F модуля вектора F внешней силы, равном F₂.

Сумма (4.410) V_в' объёмаводыm_в массой и (4.416) V_п' объёманасыщенного пара воды

m_п массойв Цл цилиндре под Пр поршнем равняется (рис.4.44) следующему значению суммарногоV_в₊_п

объёма насыщенный пар - вода на горизонтальном участке изотермы при значении F модуля вектора F внешней силы, равном F₂:

V_в₊_п = V_в' + V_п' = (m_вV_в/m) + (m_пV_п/m) ↔ V_в₊_п = [m_вV_в/(m_в+ m_п )] + [m_пV_п/(m_в+ m_п )] ↔

↔ V_в₊_п = (m_вV_в + m_пV_п)/(m_в+ m_п ) ↔ V_в₊_п = m_п[V_п+ (m_в/m_п)V_е]/m_п[1 + (m_в/m_п)] ↔

↔ V_в₊_п = [V_п+ (m_в/m_п)V_е]/[1 + (m_в/m_п)] ↔ V_в₊_п + [(m_в/m_п)V_в₊_п]= [V_п+ (m_в/m_п)V_е] ↔

↔ [(m_в/m_п)V_в₊_п] - [(m_в/m_п)V_е] = V_п - V_в₊_п ↔ m_в/m_п = (V_п - V_в₊_п) /(V_в₊_п - V_в), (4.417)

где m = m_в+ m_п - масса насыщенного пара воды в Цл цилиндре под Пр поршнем при значении

F модуля вектора F внешней силы, равном F₁, из которой на горизонтальном участке изотермы образовалась m_в массаводыи осталась m_п масса насыщенного пара воды; с другой стороны m - масса воды, которая образовалась в Цл цилиндре под Пр поршнем при значении F модуля вектора F внешней силы, равном F₃, из всего насыщенного пара.

Согласно (4.417) в равновесном двухфазномсостоянии вода - пар, которому (рис.4.44) соответствует горизонтальный участок изотермы сжатия водяногопара при T температуре, отношение m_в/m_п массы m_вводык m_п массе насыщенного пара воды численно равно отношению длины отрезка V_п - V_в+_п, который представляет собой разностьмежду V_побъёмом всегонасыщенного пара воды исуммарнымV_в+_п объёмом насыщенный пар - вода, к длине отрезка V_в+_п - V_в, который представляет собой разностьмежду суммарнымV_в+_п объёмом насыщенный пар - вода и V_в объёмом воды, полученной из всего насыщенного пара.

Выражение (4.412) применимо для расчёта отношений масс вещества, находящемся в равновесном двухфазномсостоянии, и имеет следующий вид: m_I/m_II = (V_II- V_I₊_II)/(V_I₊_II - V_I), (4.418) где m_I, m_II - массы вещества, находящемся в равновесном двухфазномсостоянии, например, m_I - масса кристалла, а m_II - масса жидкости, полученная при плавлении части кристалла; V_I - объём 1-ой фазы, когда, например, вся жидкостьпревратилась в кристалл; V_II - объём 2-ой фазы, когда, например, весь кристаллпревратился в жидкость; V_I₊_II- суммарный объём, занимаемый 1-ой и 2-ой фазой, например,кристалломи жидкостьюв равновесном двухфазномсостоянии.

Анализ равновесного двухфазного состояния вещества с помощью термодинамического потенциала Гиббса

Термодинамический G(P, T) потенциал Гиббса (4. 200) из раздела 4.1 "Физическая термодинамика"термодинамической системы при постоянных P давлении и T температуре, находящейся вравновесном двухфазномсостоянии с M₁, M₂массами фаз, имеет следующий вид: G(P, T) = M₁(t)φ₁(P, T) + M₂(t)φ₂(P, T), (4.419) где φ₁(P, T) = G₁(P, T)/M₁(t) , φ₂(P, T) = G₂(P, T)/M₂(t) - соответственно удельные термодинамические потенциалыГиббса 1-ой фазыс M₁(t) массой и 2-ой фазыс M₂(t) массой.

При фазовыхпревращенияхобщаяM масса 1-ой фазыс M₁(t) массой и 2-ой фазыс M₂(t) массой остаётся неизменной, т.е. не зависит от момента t времени, в который производят измерение этой общейM массы, поэтому имеет место следующее выражение: M = M₁(t) + M₂(t), (4.420) где M₁(t), M₂(t) - соответственно массы 1-ой и 2-ой фаз термодинамической системы, находящейся вравновесном двухфазномсостоянии, в произвольный момент t времени.

Если M₁(t) масса 1-ой фазы термодинамической системы, находящейся при постоянных

P давлении и T температуре вравновесном двухфазномсостоянии, в момент t_i времени измерения этой M₁(t_i) массы уменьшилась на ΔM величину по сравнению с M₁(t_i-1) массой в предшествующий момент t_i-1 времени, то согласно (4.415) на такую же ΔM величину увеличилась M₂(t) масса 2-ой фазы в момент t_i времени измерения этой M₂(t_i) массы по сравнению с M₂(t_i-1) массой в предшествующий момент t_i-1 времени, поэтому термодинамический G(P, T) потенциал Гиббса в данный момент

t_i времени имеет следующий вид: G(P, T) = [M₁(t_i) - ΔM]φ₁(P, T) + [M₂(t_i) + ΔM]φ₂(P, T). (4.421)

Исследование (4.421) функции G(P, T) = G термодинамического потенциала Гиббса на минимум в данный момент t_i времени по независимой переменной M₁(t_i) = M₁массой 1-ой фазы термодинамической системы, находящейся при постоянных P давлении и T температуре вравновесном двухфазномсостоянии с (4.420) M₂(t_i) = M - M₁(t_i) = M - M₁ массой 2- ой фазыэтой термодинамической системы, приводит к следующему выражению:

∂G/∂M₁ = ∂[(M₁ - ΔM)φ₁+ (M - M₁)φ₂]/∂M₁= (φ₁∂M₁/∂M₁) - (φ₂∂M₁/∂M₁) = 0 ↔ φ₁(P, T) = φ₂(P, T), (4.422) где M - общая масса вещества в термодинамической системе, находящейся при постоянных

P давлении и T температуре вравновесном двухфазномсостоянии, является для этой термодинамической системы величиной постоянной; ΔM = M₁(t_i) - M₁(t_i-1) - приращение M₁(t_i) массы 1-ой фазы термодинамической системы, находящейся при постоянных P давлении и T температуре вравновесном двухфазномсостоянии, которое в данный момент t_i временипостоянно;

φ₁= φ₁(P, T) = G₁(P, T)/M₁(t_i), φ₂= φ₂(P, T) = G₂(P, T)/M₂(t_i) - соответственно удельные термодинамические потенциалыГиббса 1-ой фазыс M₁(t_i) массой и 2-ой фазыс M₂(t_i) массой в термодинамической системе, находящейся при постоянных P давлении и T температуре вравновесном двухфазномсостоянии, которые в данный момент t_i временипостоянны.

Согласно (4.422) минимум термодинамического потенциала Гиббса у двухфазной термодинамической системы, находящейся при постоянных P давлении и T температуре, свидетельствует о равновесномсостоянии этой термодинамической системы, которое сопровождается равенствомв данный момент t_i времени φ₁(P, T), φ₂(P, T) удельных термодинамических потенциаловГиббса 1-ой и 2-ой фаз.

Уравнение P давленияв зависимости от T температурына границе раздела

2-ух фаз термодинамической системы, находящейся в данный момент t_i времени вравновесном двухфазномсостоянии, может быть получено из решения (4.422) φ₁(P, T) = φ₂(P, T) выражения относительно P давленияв f функции от T температуры, т.е. P = f(T). Например, этим P = f(T) уравнением является (рис. 4.44) горизонтальный участок изотермы на границе раздела

насыщенный пар - вода, а также этим P = f(T) уравнением является (рис. 4.46) кривая плавленияна границе раздела жидкость - твёрдое тело.

Фазовые переходы первого рода в двухфазной термодинамической системе: уравнение Клапейрона - Клаузиуса

Равенствов данный момент t_i времени (4.422) φ₁(P, T) = φ₂(P, T), т.е.φ₁= φ₂, удельных термодинамических потенциаловГиббса на границе раздела 1-ой и 2-ой фаз в термодинамической системе, находящейся вравновесном двухфазномсостоянии, но различиеих следующих первых производных по независимымP давлению и T температуре свидетельствует о фазовом переходе первого рода: (∂φ₁/∂T)_P ≠ (∂φ₂/∂T)_P; (∂φ₁/∂P)_T ≠ (∂φ₂/∂P)_T, (4.423) где индексы _"_P_", _"_T_" при первых производных означают, что при определении частной производной по независимойT температуре постояннымпараметромявляется P давление, а при определении частной производной по независимомуP давлению постояннымпараметромявляется T температура.

Характерной особенностью фазовых переходов первого рода является поглощениеили выделениетеплоты при их осуществлении. К фазовым переходам первого родаотносятся превращения при испарении, конденсации, плавлениии кристаллизациивещества.

Цикл (рис.4.19) из раздела 4. 1 "Физическая термодинамика" Карно включает

(рис. 4.45) горизонтальные 1-2, 3-4 участки изотермы, в пределах которых происходит постоянный равновесныйпроцесс перехода молекул из жидкостив насыщенный пар и обратнопо (4.422) фазовому переходу первого рода, и две 2-3, 4-1 адиабаты.

В результате изотермического1-2 процесса от нагревателяс T температурой происходит передача рабочему телуQ₁теплоты, в результате чего из 1- го состояния жидкость, т.е. 1-ая фаза,

m массой V_I объёмом испаряется и превращается в насыщенный парP_н.п_. давлением. В результате изотермического 1-2 процесса во 2- ом состоянии вся жидкость в результате равновесногоизотермического расширения при T температуре и P_н.п_. давлении 2-ух фаз термодинамической системы жидкость- насыщенный пар переходит в фазовое состояние насыщенный пар m массой

V_II объёмом.

В результате 2-3 процесса происходит (4.68) из раздела 4. 1 "Физическая термодинамика" адиабатическое расширение насыщенного пара, сопровождающееся уменьшением его температуры от T до T-dT значения иуменьшением его давления от P_н.п до P_н.п.- dP_н.п значения.

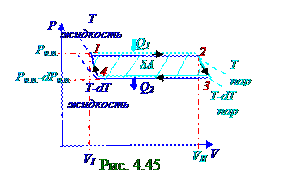
В результате изотермического3-4 процесса холодильникус T-dT температурой передаётся от рабочего телаQ₂ теплота, в результате чего из 3- го состояния насыщенный пар, т.е. 2 -ая фаза, m массой V_II объёмом конденсируется и превращается в жидкостьP_н.п.- dP_н.п давлением. В результате изотермического 3-4 процесса во 4 - ом состоянии весь насыщенный пар в результате равновесногоизотермического сжатия при T-dT температуре и

P_н.п.-P_н.п давлении 2-ух фаз термодинамической системы насыщенный пар - жидкость переходит в фазовое состояние m массой V_I объёмом.

В результате 4-1 процесса происходит (4.68) из раздела 4. 1 "Физическая термодинамика" адиабатическое сжатие жидкости, сопровождающееся увеличением его температуры от T-dT до

T значения иувеличением его давления от P_н.п.- dP_н.п до P_н.п значения.

КПД (4.123) из раздела 4.1 "Физическая термодинамика" (рис. 4.45) тепловой машины вциклическом процессе имеет следующий вид: η = δA/Q₁, (4.424)

где δA - работа, выполненная рабочим телом - насыщенным паром в циклическом процессе при его переходе из 1- го в 3- ье состояние и затем возвращения из 3- го в 1- ое состояние, численно равна заштрихованной площади между горизонтальными 1-2, 3-4 участками изотермы и 2-3, 4-1 адиабатами. Эта заштрихованная площадь, вследствие (рис. 4.45) малости приращения dT, dP_н.п соответственно температуры и давлении 2-ух фаз термодинамической системы жидкость- насыщенный пар между 2 - мя горизонтальными 1-2, 3-4 участками изотермы, приблизительноравна площади заштрихованногопрямоугольника, поэтому δA работа, выполненная рабочим телом - насыщенным паром в циклическом процессе имеет следующий вид: δA = P(V_II - V_I ) - (P -dP)(V_II - V_I ) ↔ ↔ δA = dP(V_II - V_I ) = dP(mv₀_II - mv₀_I) = m(v₀_II - v₀_I)dP, (4.425) где dP - малое приращение давления в термодинамической системе, находящейся вравновесном двухфазномсостоянии; V_II - объёмнасыщенного пара m массой, который вследствие (рис.4.45) малости приращения dT, dP_н.п соответственно температуры и давлении 2-ух фаз термодинамической системы жидкость- насыщенный пар между 2 - мя горизонтальными 1-2, 3-4 участками изотермы, приблизительно одинаков в 2, 3 состояниях на 2-3 адиабате; V_I - объёмжидкости m массой в

4, 1 состояниях на 4-1 адиабате, равной m массе насыщенного пара V_II объёмом в 2, 3 состояниях на 2-3 адиабате, поскольку вся эта m масса насыщенного пара превратилась в результате равновесногоизотермического сжатия в равную m массу жидкости; v₀_II = V_II /m, v₀_I = V_I /m - удельные(4.2) из раздела 4.1 "Физическая термодинамика" объёмы соответственно насыщенного пара и жидкости.

Согласно(4.137) из раздела 4. 1 "Физическая термодинамика" первой теореме Карно

η_к термический КПДтепловой машины, совершающий цикл Карно, не зависит от состава рабочего телаи выражается следующей формулой: η_к = (T₁- T₂)/T₁= [T - (T-dT)]/ T = dT/ T, (4.426) где T₁= T, T₂= T-dT - для цикла Карно(рис. 4.44)температурасоответственнонагревателяи холодильника.

Подставляем (4.420) в (4.419) и получаем η КПД (4.123) из раздела 4.1 "Физическая термодинамика" (рис. 4.44) тепловой машины вциклическом процессе, который имеет следующий вид: η = δA/Q₁= m(v₀_II - v₀_I)dP/Q₁. (4.427)

Выражение (4.427) справедливо для расчёта η КПД любой тепловой машины вциклическом процессе и в том числе (рис. 4.45) для расчёта η КПД тепловой машины, совершающей цикл Карно, поэтому из приравнивания (4.426), (4.427) получаем следующее уравнение Клапейрона - Клаузиуса, устанавливающее зависимость первой производной P давления от T температуры в термодинамической системе, находящейся вравновесном двухфазномсостоянии: η_к = η ↔ dT/ T = m(v₀_II - v₀_I)dP/Q₁↔ dP/dT = Q₁/mT(v₀_II - v₀_I) ↔ dP/dT = q/T(v₀_II - v₀_I), (4.428) где q = Q/m > 0 - удельнаятеплота, переданнаятермодинамической системе, находящейся вравновесном двухфазномсостоянии, от нагревателяс T температурой; q = Q/m < 0 - удельнаятеплота, переданнаяот термодинамической системе, находящейся вравновесном двухфазномсостоянии, холодильнику с T температурой.

Знак (4.428) первой производной P давления от T температуры зависит от знака q удельнойтеплоты: он положителен, если теплота подводится, и отрицателен, если теплота отводитсяот термодинамической системы, находящейся вравновесном двухфазномсостоянии. Знак (4.428) первой производной P давления от T температуры зависит также от численных значений положительныхвеличин удельных v₀_I, v₀_II объёмов 1-ой и 2-ой фаз термодинамической системы, находящейся вравновесном двухфазномсостоянии. Например, при плавлениильда, т.е. когда удельнаяq теплота, переданнаятермодинамической системе, больше нуля, удельный v₀_II объём получившейся воды меньше по величинеудельного v₀_I объёма тающего льда. Поэтому

(рис. 4.46) график зависимости P давленияот T температурына границе раздела 2-ух фаз термодинамической системы, т.е.лёд - вода, находящейся в данный момент t_i времени вравновесном двухфазномсостоянии, имеет угол больше 90º к оси абсцисс, по которой нанесены значения

T температуры.

Диаграммы состояний при фазовых переходах в термодинамической системе

Диаграммами состояний, которые строят экспериментальнодля разных веществ, называют (рис.1.1) из раздела 1.0 "Физические основы механики" прямоугольную декартову систему координат, в которой по OY оси указывают T температуру, а по OZ оси указывают P давление, разделённую на три области: твёрдая, жидкая и газовая фазы. Границами этих соприкасающихся фазявляются (рис. 4.46) графические зависимости сублимации, испаренияи плавления, на которых в термодинамическом равновесиисуществуют соответственно твёрдая и газообразная, жидкая и газообразная, а также твёрдая и жидкая фазывещества.

Пунктиром нарис. 4.46 показана графическая зависимость плавлениядля веществ, у которых (4.428) первая производная P давления от T температуры отрицательна, т.е. dP/dT < 0, например, для воды.

На диаграмме (рис. 4.46) состояний Тр точкой отмечают трёхфазноесостояние вещества, в которой в термодинамическом равновесиисуществуют твёрдая, газообразная и жидкая фазывещества. Например, для воды термодинамическоеравновесиельда, пара и жидкости, т.е.трёх фаз, существует приP давлении и T температуре, равных соответственно 610 Па и 0, 008º C. На диаграмме (рис. 4.46) состояний Тр' точкой отмечают начало вилки: левая графическая зависимость является границей

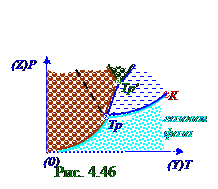
между двумя твёрдыми фазами, например, α - и β -фазами, а правая графическая зависимость является границеймежду твёрдойβ - фазойвещества и жидкой фазойэтого вещества.

На диаграмме (рис.4.46) К точкой отмечают (рис.4.14) из раздела 4.1 "Физическая термодинамика" критическое состояние, где исчезает различие между газообразной и жидкой фазами.

Фазовые переходы второго рода в двухфазной термодинамической системе

Фазовые переходы второго родапроисходят тогда, когда равныв данный момент t_i времени первые производные по независимымP давлению и T температуре(4.414) φ₁(P, T), φ₂(P, T) удельных термодинамических потенциаловГиббса на границе раздела 1-ой и 2-ой фаз в термодинамической системе, находящейся вравновесном двухфазномсостоянии, т.е. когда выполняются следующие соотношения: (∂φ₁/∂T)_P = (∂φ₂/∂T)_P; (∂φ₁/∂P)_T = (∂φ₂/∂P)_T, (4.429)

где индексы _"_P_", _"_T_" при первых производных означают, что при определении частной производной по независимойT температуре постояннымпараметромявляется P давление, а при определении частной производной по независимомуP давлению постояннымпараметромявляется T температура.

Фазовые переходы второго рода математически описаны в 1933 г. физиком - теоретиком П.Эренфестом и позволяют определить следующие выражения первых производных P давления от

T температуры, т.е. dP/dT, при равновесном фазовомпереходе второго родав термодинамической системе: dP/dT = (C_pII- C_pI)/T[(∂v₀_II /∂T)_P - (∂v₀_I /∂T)_P];

dP/dT = (∂v₀_II /∂T)_P - (∂v₀_I /∂T)_P /T[(∂v₀_II /∂P)_T - (∂v₀_I /∂P)_T] (4.430)

где C_pII- C_pI - разность междумолярнымитеплоемкостямипри (4.57) из раздела 4.1 "Физическая термодинамика" постоянномP давлении соответственно 2-ой и 1-ой фаз термодинамической системы, гдепроисходитравновесный фазовыйпереход второго рода;(∂v₀_II /∂T)_P = v₀_II α _P₂;

(∂v₀_I /∂T)_P = v₀_I α _P₁- температурные коэффициенты удельного(4.2) из раздела 4. 1 "Физическая термодинамика" объёмного расширения при (4.15) из раздела 4.1 "Физическая термодинамика" постоянномP давлении соответственно 2-ой и 1-ой фаз термодинамической системы, гдепроисходитравновесный фазовыйпереход второго рода; (∂v₀_II /∂P)_T= - v₀_II β_T₂; (∂v₀_I /∂P)_T = v₀_I β_T ₁- коэффициенты удельной(4.2) из раздела 04. 1.0 "Физическая термодинамика" сжимаемости при (4.14) из раздела 4.1 "Физическая термодинамика" постояннойT температуре соответственно

2-ой и 1-ой фаз термодинамической системы, гдепроисходитравновесный фазовыйпереход второго рода.

Примерами равновесных фазовыхпереходов второго родав термодинамических системах являются следующие переходы:

- переход некоторых веществ при низких температурах в сверхпроводящеесостояние;

- переход железа (7.127) из раздела 7.2 "Магнитостатика"из ферромагнитногов парамагнитноесостояние в температурной точке Кюри;

- превращение жидкогоHeI в жидкийHeII при T температуре, равной 2,2 К, что используется для получения сверхнизкихтемператур, равных десятым долям по шкале (4.13) из раздела 4.1 "Физическая термодинамика" температурКельвина.

Отличительные черты кристаллического состояния. Классификация кристаллов. Физические типы кристаллических решёток

Подавляющее большинство твёрдых телимеет кристаллическое строение, т.е. упорядоченное расположение частиц (атомов, ионов, молекул), из которых они образованы. С такой структурой кристалловсвязано свойствоанизотропии, которая проявляется в зависимости ряда физических свойств от направления.

Эти свойства не всегда проявляются, поскольку кристаллическиетела встречаются, как правило, в виде поликристаллов - совокупности множества беспорядочно расположенных мелких кристалликов. Искусственно с помощью специальных условий можно получить из раствора большие монокристаллы. Последние встречаются и в природе у некоторых минералов.

Кристаллической решёткеприсущи различные виды симметрии, т.е. свойства решётки совпадать с самой собой при некоторых мысленных пространственных перемещениях(например, поступательныхи поворотах). Любая идеальная кристаллическая решёткапрежде всего характеризуется трансляционной симметрией. Это означает, что каждой решётке можно сопоставить (рис. 4.47) три некомпланарныхэлементарных a, b, c вектора. При мысленном перемещении идеальной кристаллической решётки вдоль каждого из этих векторов она совмещается с себе подобной соседней кристаллической решёткой. Параллелепипед, построенный на a, b, c векторах, называют (рис. 4.47) элементарной ячейкой, а a, b, c модули этих векторов - периодами идентичности решётки вдоль соответствующих направлений этих a, b, c векторов. Элементарную ячейкуможно выбрать различными способами. Если она включает наименьшеек

⇐ Предыдущая 1 2 3 4 56