Лекция 17 4 страница

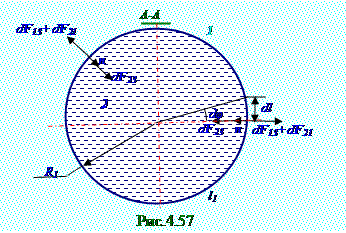
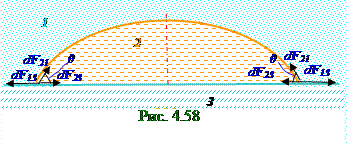
где отрицательноеdF₂₁cosθ значение проекции вектора dF₂₁силыповерхностного натяжения, действующего на dl элементарный участок контура для случая (рис. 4.57) 2 жидкости, несмачивающей поверхность 3 твёрдого тела, учитываетсязнаком cosθ, т.к. для (рис.4. 56)несмачивающейжидкости краевой угол имеет значения π/2 < θ < π; положительноеdF₂₁cosθ значение проекции вектора dF₂₁силы (рис. 58)

2 жидкости, смачивающей поверхность 3 твёрдого тела, учитываетсязнаком cosθ, т.к. для смачивающейжидкости краевой угол имеет значения 0 < θ < π/2.

Подставляем значения модулей dF₂₁ = σ₂₁dl из (4.436), dF₁₃ = σ₁₃dl из (4.437) и dF₂₃ = σ₂₃dl из (4.438) в выражение (4.440) и получаем следующее соотношение θ краевого угла с σ₂₁, σ₁₃и σ₂₃ коэффициентами поверхностного натяжения: σ₂₁cosθ dl - σ₁₃dl + σ₂₃dl = 0 ↔ ↔ cosθ = (σ₁₃- σ₂₃)/σ₂₁. (4.441) Из анализа (4.441) следует: если σ₁₃коэффициент поверхностного натяженияна границе раздела 1 газ-3 твёрдое телобольше σ₂₃ коэффициента поверхностного натяженияна границе раздела 2 жидкость -3 твёрдое телои кроме этого [(σ₁₃- σ₂₃)/σ₂₁] ≤ 1, то существуетусловие устойчивого равновесия 2 жидкостина 3 твёрдом теле, окружённым 1 газом, и cosθ ≥ 0, а θ ≤ π/2. Это случай смачивающейжидкости (рис. 4.58), (рис. 4.59), например, капля 2 керосинана поверхности 3 стекла, находящиеся в воздухе. Если в (4.441) выражение σ₁₃ коэффициента поверхностного натяженияна границе раздела 1 газ-3 твёрдое теломеньше σ₂₃ коэффициента поверхностного натяженияна границе раздела 2 жидкость - 3 твёрдое тело и кроме этого |(σ₁₃- σ₂₃)/σ₂₁| ≤ 1, то существуетусловие устойчивого равновесия 2 жидкости на 3 твёрдом теле, окружёнными 1 газом, и cosθ ≤ 0, а π/2 ≤ θ ≤ π. Это случай несмачивающей жидкости (рис.4. 56), (рис.4. 57), например, капля 2 водына поверхности 3парафина, находящиеся в воздухе.

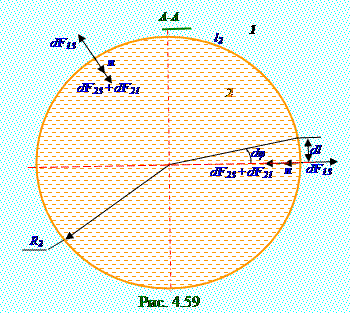
Капиллярный эффект. Формула Лапласа для поверхностного натяжения, дополнительное давление, создаваемое сферической поверхностью жидкости.

P_o

Капиллярный эффектдля(рис.4.60) 2 смачивающей жидкостиповерхности 3 материала капиллярнойтрубки с малым r радиусом, опущеннойвоткрытый сосуд с этой 2 жидкостью,проявляется в превышении уровня 2 жидкости вкапиллярнойтрубке надуровнем 2 жидкости в открытом сосуде на h₁величину.Капиллярный эффектдля(рис.4. 61)

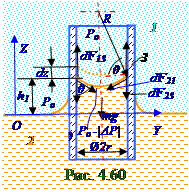
2 несмачивающей жидкостиповерхности 3 материала капиллярнойтрубки с малым r радиусом, опущеннойвоткрытый сосуд с этой 2 жидкостью,проявляется в понижении уровня 2 жидкости вкапиллярнойтрубке относительноуровня 2 жидкости в открытом сосуде на h₂величину.

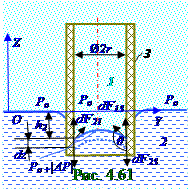
В случае (рис.4. 60)2 смачивающей жидкостипри превышении уровня этой2 жидкости в капиллярнойтрубки на dz величину над h₁уровнем 2 жидкости в капиллярнойтрубки площадь поверхности соприкосновения 2 жидкости с 1 газомне меняется, т.е. приращение dS_пов площади поверхности соприкосновения 2 жидкости с 1 газомв выражении (4.435) равно нулю. В случае (рис.4. 61) 2 несмачивающей жидкости при понижении уровня этой2 жидкости в капиллярнойтрубки на dy величину относительно уровня 2 жидкости в капиллярнойтрубки площадь поверхности соприкосновения 2 жидкости с 1 газомне меняется, т.е. приращение dS_пов площади поверхности соприкосновения 2 жидкости с 1 газомв выражении (4. 435) равно нулю.

Поэтому в случае (рис. 60)2 смачивающей или (рис. 4.61)несмачивающей 2 жидкостиповерхности 3 материала капиллярнойтрубки (4.435) δA₂₁элементарная работа, выполняемая вектором dF₂₁ силы поверхностного натяжения, который действует на dl элементарный участок контура и направлен по касательнойк сферической поверхности (рис. 4.58) 2 смачивающей жидкости или (рис.4.56) 2 несмачивающей жидкости в сторону уменьшения площади раздела этой 2 жидкости -1 газа, равна нулю.

Согласно при равенстве нулю δA₂₁элементарной работы, выполненной dF₂₁вектором силы поверхностного натяженияна поверхности раздела (рис.4. 60) 2 смачивающей жидкости или (рис.4. 61) 2 несмачивающей жидкости с 3 твёрдым телом, будет равно нулюdW_p₂₁элементарное приращение W_p₂₁потенциальнойэнергии поверхности раздела этих 2 смачивающей жидкости или 2 несмачивающей жидкости с1 газом, т.е. выражение (4.435) будет иметь следующий вид: dW_p₂₁ = 0. (4.442) В случае (рис.4.60)2 смачивающей жидкости при превышении уровня на dz величину над h₁уровнем 2 жидкости в капиллярнойтрубки площадь поверхности соприкосновения 2 жидкости со стенкой 3 материала капиллярнойтрубки увеличивается на dS величину.

Поэтому в случае (рис.4.60)2 смачивающей жидкости поверхности 3 материала капиллярнойтрубкисогласно (4.435) dW_p₂₃элементарное приращение W_p₂₃потенциальной энергии поверхности раздела 2 смачивающей жидкости со стенкой 3 материала капиллярнойтрубки будет иметь следующий вид: dW_p₂₃ = σ₂₃dS_пов = 2πrσ₂₃dz, (4.443) где 2πrdz = dS -положительное приращение площади поверхности соприкосновения 2 жидкости со стенкой 3 материала капиллярнойтрубки rрадиусомпри превышении уровня 2 жидкости в капиллярнойтрубки на dz величину над h₁уровнем этой 2 жидкости в капиллярнойтрубке.

В случае (рис.4.60)2 смачивающей жидкости при превышении уровня на dz величину над h₁уровнем 2 жидкости в капиллярнойтрубки площадь поверхности соприкосновения 1 газа со стенкой 3 материала капиллярнойтрубки уменьшается на dS величину.

Поэтому в случае (рис. 4.60)2 смачивающей жидкости поверхности 3 материала капиллярнойтрубкисогласно (4.435) dW_p₁₃элементарное приращение W_p₁₃ потенциальной энергии поверхности раздела 1 газа со стенкой 3 материала капиллярнойтрубки будет иметь следующий вид: dW_p₁₃ = - σ₁₃dS = - 2πrσ₁₃dz, (4.444) где "-2πrdz = dS " -отрицательное приращение площади поверхности соприкосновения 1 газа со стенкой 3 материала капиллярнойтрубки rрадиусомпри превышении уровня 2 жидкости в капиллярнойтрубки на dz величину над h₁уровнем 2 смачивающей жидкостив капиллярнойтрубке.

В случае (рис.4.60)2 смачивающей жидкости поверхности 3 материала капиллярнойтрубки dW_p₂элементарное приращение W_p₂потенциальной энергии согласно (1.97) из раздела 1.0 "Физические основы механики" при превышении уровня 2 смачивающей жидкости в капиллярнойтрубки на dz величину над h₁уровнем этой 2 смачивающей жидкости в капиллярнойтрубке имеет следующий вид: dW_p₂= πr²ρh₁g dz, (4.445) где πr²ρh₁= m - масса 2 смачивающей жидкости ρ плотностью в капиллярнойтрубке rрадиусом, имеющим h₁высоту над уровнем этой 2 смачивающей жидкости в капиллярнойтрубке.

В случае (рис.4.60)2 смачивающей жидкости поверхности 3 материала капиллярнойтрубки полное dW_p приращение W_pпотенциальной энергии при превышении уровня 2 смачивающей жидкости в капиллярнойтрубки на dz величину над h₁уровнем этой 2 смачивающей жидкости в капиллярнойтрубке с учётом (4.4442), (4.443), (4.444) и (4.445) имеет следующий вид:

dW_p = dW_p₂₁+ dW_p₂₃ + dW_p₁₃ + dW_p₂ = 2πrσ₂₃dz - 2πrσ₁₃dz+ πr²ρh₁gdz=

= 2πr( σ₂₃ - σ₁₃)dz + πr²ρh₁gdz ↔ dW_p/dz =2πr( σ₂₃ - σ₁₃) + πr²ρh₁g, (4.446) гдеdW_p₂₁ = 0 - (4.442) dW_p₂₁элементарное приращение W_p₂₁потенциальнойэнергии поверхности раздела 2 смачивающей жидкости с1 газом, равное нулю;dW_p₂₃= 2πrσ₂₃dz - (4.443) элементарное приращение W_p₂₃потенциальной энергии поверхности раздела 2 смачивающей жидкости со стенкой 3 материала капиллярнойтрубки; dW_p₁₃ = - 2πrσ₁₃dz -(4.444) элементарное приращение W_p₁₃потенциальной энергии поверхности раздела 1 газа со стенкой 3 материала капиллярнойтрубки; dW_p₂= πr²ρh₁g dz- (4.445) элементарное приращение W_p₂потенциальной энергии при превышении уровня 2 смачивающей жидкости в капиллярнойтрубки на dz величину над h₁уровнем этой 2 смачивающей жидкости в капиллярнойтрубке.

В случае (рис.4.60)2 смачивающей жидкости поверхности 3 материала капиллярнойтрубки значение h₁ превышения уровня этой 2 смачивающей жидкости в капиллярнойтрубке относительно уровня в открытом сосуде при p_o давлении газа в окружающей среде определим из минимума W_pпотенциальнойэнергии столба 2 смачивающей жидкости h₁высотой в капиллярнойтрубке, т.е. приравняв выражение (4.446) нулю, вследствие чего имеет место следующее выражение:

dW_p/dz = 2πr( σ₂₃ - σ₁₃) + πr²ρh₁g = 0 ↔ h₁ = 2(σ₁₃ - σ₂₃)/ρgr. (4.447) Преобразуем выражение (4.441), из которого рассчитывается θ краевой угол (рис.4.56) и (рис. 4.58), (рис.4.60) и (рис.4.61) по величинам коэффициентов σ₂₁, σ₁₃ и σ₂₃ поверхностного натяженияна границах разделасоответственносферической поверхности раздела 2 смачивающей жидкости или 2 несмачивающей жидкости-1 газ, плоской поверхности раздела 1 газ - 3 твёрдое тело, плоской поверхности раздела 2 смачивающей жидкости или 2 несмачивающей жидкости-3 твёрдое тело, вследствие чего имеет место следующее соотношение: (σ₁₃- σ₂₃) = σ₂₁cosθ. (4.448) Подставим (4.448) в (4.447) и получим следующее выражение, которое называется формулой Лапласа,для расчёта при значении θкраевого угла θ ≤ π/2 положительного (рис.4.60) значения h₁ высоты подъёма уровня 2 смачивающей жидкости в 3 материале капиллярнойтрубке относительно уровня в открытом сосуде при P_o давлении 1 газа в окружающей среде:

h₁ = 2σ₂₁cosθ/ρgr, (4.449) где σ₁₂ - коэффициент поверхностного натяженияна границе раздела (рис.4.56) и

(рис. 4.60) сферической поверхности 2 смачивающей жидкости -1 газ; r - малый радиус капиллярнойтрубки; R = r/cosθ - радиус(рис. 4.60) сферической поверхности раздела

2 смачивающая жидкость -1 газ.

Выражение (4.449) формулы Лапласа справедливодля расчёта отрицательного (рис. 4.61) h₂значения понижения уровня жидкости в капиллярнойтрубке относительно уровня в открытом сосуде при P_o давлении газа в окружающей среде в случае 2 несмачивающей жидкостиповерхности

3 материала капиллярнойтрубки при θзначении краевого угла π/2 ≤ θ≤ π.

В случае (рис. 4.60)2 смачивающей жидкости поверхности 3 материала капиллярнойтрубки P_o давление в капиллярена уровне OY оси, т.е. на уровне жидкости в открытом сосуде, согласно закону Паскаляравно P_o давлению в газе, окружающему 3 материал капиллярнойтрубки и

2 смачивающая жидкость. Из баланса давления, равного P_o в 3 материале капиллярнойтрубки на уровне OY оси, т.е. уровне 2 смачивающей жидкости в открытом сосуде, с учётом P_o - ΔP давления под поверхностнойплёнкой на границе раздела2 смачивающая жидкость-1 газ, а также с учётом (4.449) h₁значения высоты подъёма уровня 2 смачивающей жидкости ρ плотностью в 3 материале капиллярнойтрубки относительно уровня в открытом сосуде, получается следующее выражение: P_o = P_o - ΔP + ρgh₁ ↔ P_o = P_o - ΔP +ρg2σ₂₁cosθ/ρgr ↔ ΔP = 2σ₂₁cosθ /r= 2σ₂₁ /R, (4.450) где ΔP - дополнительноедавление под поверхностнойплёнкой на границе раздела2 смачивающая жидкость-1 газ, выведенное Лапласом; R = r/cosθ - радиус сферической поверхности раздела

2 смачивающая жидкость -1 газ.

Согласно (4.450) в случае (рис. 4.60)2 смачивающей жидкости поверхности 3 материала капиллярнойтрубки, когда θ значение краевого угла θ ≤ π/2, значение ΔP дополнительногодавления под поверхностнойплёнкой на границе раздела2 смачивающая жидкость -1 газ больше нуля, т.е. ΔP > 0. Поэтому значениеP_o - ΔP результирующего давления под поверхностнойплёнкой на границе раздела2 смачивающая жидкость -1 газ меньше P_o давления в газе, окружающем

3 материал капиллярнойтрубкии 2 смачивающую жидкость, на величину ΔP = 2σ₂₁cosθ /r. Этим объясняетсявогнутая(рис. 4.60) поверхностнаяплёнка в сторону 2 смачивающей жидкостина границе раздела2 смачивающая жидкость3 материала капиллярнойтрубки-1 газ.

Согласно (4.450) в случае 2 несмачивающей жидкостиповерхности 3 материала капиллярнойтрубки, когда (рис.4.61) θ значениекраевого угла π/2 ≤ θ ≤ π, значение ΔP дополнительногодавление под поверхностнойплёнкой на границе раздела2 несмачивающая жидкость-1 газменьше нуля, т.е. ΔP < 0. Поэтому P_o - ΔP значение результирующего давления под поверхностнойплёнкой на границе раздела2 несмачивающая жидкость-1 газбольше P_o давления в газе, окружающем

3 материал капиллярнойтрубкии 2 несмачивающую жидкость, на величину ΔP = 2σ₂₁cosθ /r. Этим объясняетсявыпуклая (рис. 4.60) поверхностнаяплёнка в сторону 1 газа на границе раздела

2 несмачивающая жидкость3 материала капиллярнойтрубки-1 газ.

Введение (4.450) |ΔP| модуля ΔP дополнительного давления, позволяет упростить объяснение наличия вогнутой(рис.4.60) поверхностнойплёнки в сторону 2 смачивающей жидкостина границе раздела 2 смачивающая жидкость3 материала капиллярнойтрубки-1 газ, когда P_o - |ΔP| значение результирующего давления под поверхностнойплёнкой на границе раздела2 несмачивающая жидкость 3 материала капиллярнойтрубки-1 газ меньше P_o давления в газе.

При введении (4.450) |ΔP| модуля ΔP дополнительного давления выражение для результирующего давления под выпуклой(рис.4.61)поверхностнойплёнки в сторону 1 газа принимает следующий вид: P_o+|ΔP|, что упрощает объяснение наличия выпуклой поверхностнойплёнки в сторону 1 газа на границе раздела2 несмачивающая жидкость3 материала капиллярнойтрубки-1 газ.

Анализ равновесного состояния границы раздела между фазами вещества с помощью термодинамического потенциала Гельмгольца

Элементарная δAработа, которую выполняет над внешними телами равновеснаятермодинамическая система с постоянным значением P давления при элементарном dV приращении её объема и в которой существует граница раздела (рис.4.46) между фазами веществаэтойтермодинамической системы, имеет следующий вид: δA = δA₀+ δA_ф = PdV - σdS_пов, (4.451) где δA₀= PdV - элементарное приращение (4.12) из раздела 4.1 "Физическая термодинамика"работы, выполненной термодинамической системой над внешними телами, вещество которой состоит из одной фазы, т.е отсутствует граница раздела между фазами; δA_ф = - σdS_пов - элементарное приращение (4.434) работы, выполненной силами поверхностного натяженияна границе раздела между фазами веществаэтойтермодинамической системы; σ[Н/м] - коэффициент поверхностного натяжения на границе раздела между фазами веществатермодинамической системы.

Согласно (4.451) прирасширениитермодинамической системы, т.е. когда dV > 0 и δA₀= PdV > 0, вследствие увеличения S_пов площади поверхности границы раздела (рис.4.46) между фазами вещества, т.е. dS_пов >0 и δA_ф = - σdS_пов< 0, часть δA₀работы этойтермодинамической системы, которая была бы превращена в положительнуюработу над внешними телами и которая равна σdS_пов, расходуется на преодоление сил (рис.4.46) поверхностного натяжения на границе раздела между фазами вещества, из которых состоит термодинамическая система. Поэтому в термодинамической системе, в которой существует граница раздела (рис. 4.46) между фазами вещества, часть элементарнойδA₀работы, которая была бы превращена в положительнуюработу над внешними телами, превращается при расширении(4.428) в σdS_пов элементарное приращение свободной поверхностной энергии на границе фаз этойтермодинамической системы. Элементарная(4.434) δAработа, которую выполнит в этом случае над внешними телами равновеснаятермодинамическая система, будет на величину

σdS_пов элементарного приращения свободной поверхностной энергии на границе меньше по сравнению с равновеснойтермодинамической системой, которая состоит из одной фазы, т.е в которой отсутствует граница раздела между фазами этойтермодинамической системы.

Элементарная δA'работа, которую выполняет внешние тела над равновеснойтермодинамической системой с постоянным значением P давления при элементарном dV приращении её объема и в которой существует граница раздела (рис. 4.46) между фазами веществаэтойтермодинамической системы, имеет следующий вид: δA' = δA₀' + δA_ф' = -PdV + σdS_пов, (4.452) где δA₀' = -PdV - элементарное приращение (4.12) из раздела 4.1 "Физическая термодинамика"работы, выполненной внешними телами над равновеснойтермодинамической системой, вещество которой состоит из одной фазы, т.е отсутствует граница раздела между фазами; δA_ф' = σdS_пов - элементарное приращение (4.433) работы, выполненной внешними телами на границе раздела между фазами веществатермодинамической системы; σ[Н/м] - коэффициент поверхностного натяжения на границе раздела между фазами веществатермодинамической системы.

Согласно (4.452) присжатиитермодинамической системы, т.е. когда dV < 0 и δA₀' = -PdV > 0, вследствие уменьшения S_пов площади поверхности границы раздела (рис. 4.46) между фазами вещества, т.е. dS_пов < 0 и δA_ф' = σdS_пов< 0, частью δA₀' работы внешних тел, которая была бы превращена в положительнуюработу этих внешних тел над равновеснойтермодинамической системой и которая равна σdS_пов, является приобретённое прирасширении σdS_пов элементарное приращение свободной поверхностной энергии на границе фаз этойтермодинамической системы. Поэтомуэлементарная(4.452) δA'работа, которую выполнит в этом случае внешние тела присжатиитермодинамической системы при переводе её из одного равновесногосостояния в другое, будет на величину (4.451) приобретённого прирасширении σdS_пов элементарного приращения свободной поверхностной энергии на границе раздела (рис. 4.46) между фазами вещества меньше по сравнению с равновеснойтермодинамической системой, которая состоит из одной фазы, т.е. в которой отсутствует граница раздела между фазами этойтермодинамической системы.

⇐ Предыдущая 1 2 345 6 Следующая ⇒