Лекция 17 1 страница

04.3.0 Физическая термодинамика - 2 часа

Лекция 17

Агрегатные состояния вещества. Условия равновесия фаз: отношение масс вещества, находящемся в равновесном двухфазном состоянии. Анализ равновесного двухфазного состояния вещества с помощью термодинамического потенциала Гиббса. Фазовые переходы первого рода в двухфазной термодинамической системе: уравнение Клапейрона - Клаузиуса. Диаграммы состояний при фазовых переходах в термодинамической системе. Фазовые переходы второго рода в двухфазной термодинамической системе. Критические явления при фазовых переходах в термодинамической системе. Отличительные черты кристаллического состояния твёрдых тел. Классификация кристаллов твёрдых тел. Физические типы кристаллических решёток твёрдых тел. Дефекты в кристаллах твёрдых тел. Теплоёмкость кристаллов твёрдых тел.

Основные представления о строении жидкостей. Поверхностное натяжение и свободная поверхностная энергия. Равновесие смачивающей и несмачивающей капель жидкости на поверхности твердого тела. Капиллярный эффект. Формула Лапласа для поверхностного натяжения, дополнительное давление, создаваемое сферической поверхностью жидкости. Анализ равновесного состояния границы раздела между фазами вещества с помощью термодинамического потенциала Гельмгольца. Анализ равновесного состояния границы раздела жидкость - газ с помощью термодинамического потенциала Гельмгольца. Применение термодинамического потенциала Гельмгольца для определения температурной зависимости коэффициента поверхностного натяжения жидкости

Агрегатные состояния вещества. Условие равновесия фаз: отношение масс вещества, находящемся в равновесном двухфазном состоянии

Термодинамическийметод применим для описания не только однородныхпо физику - химическому составу сред, но и систем, состоящих из нескольких пространственно разнесённых частей, между которыми существует граница раздела. Проще всего описывать термодинамические системы, у которых составные части находятся в равновесныхсостояниях, а через границы раздела не происходит перенос вещества, энергии и импульса. Такая термодинамическая система является равновесной и для неё применимы методы равновесной термодинамики.

Если составные части термодинамической системы не находятся между собой в равновесии, то возникают термодинамическиепотоки через границы их раздела. Считая происходящие в системе процессы квазистатическими, а потоки малыми, можно использовать методы равновесной термодинамики и для неравновесной системы.

При описании пространственно неоднородныхсред применимо разбиение их на некоторое число однородныхпо своему составу частей, разделённых границами раздела. Макроскопическая часть среды, т.е. вещества, имеющая однородный физико - химический состав, называется фазой. Далее рассматриваются термодинамические системы, для описания состояния фаз которых применимы методы равновесной термодинамики.

Если среда однородна по всему своему объёму, то такая термодинамическая система будет однофазной, а если система состоит из двухили болееграничащих между собой однородных сред, то это двухфазнаяили многофазная термодинамическая система. Примером двухфазнойсистемы может служить стеклянный сосуд с налитой в него водой. В этом случае в системе имеются жидкаяи твёрдая фазы, которыми являются соответственно вода и стекло. Если в состав системы включить окружающий сосуд воздух, то она станет трёхфазнойсистемой. Смесь газов является однофазной системой, т.к. в этой смеси нет границы раздела.

Для равновесия фазнеобходимо, чтобы между ними наблюдалось тепловоеи механическоеравновесие. Первое из этих условий означает равенство T₁ и T₂ температур с разных сторон границы раздела фаз, т.е. T₁ = T₂ = T. Второе условие не обязательно соответствует равенству(4.1) из раздела

4. 1 "Физическая термодинамика" P₁ и P₂давлений с разных сторон границы раздела, т.к. сама граница, если она не является плоской, может создавать дополнительное межфазноедавление.Поэтому в общемслучае условие механическогоравновесия имеет следующий вид:

P₂= P₁+ ΔP₁₂, (4. 413)

где ΔP₁₂- дополнительное давление на первуюфазу, создаваемое границей её раздела со второй. Если считать границуфаз плоской, то(4.413) условие будет эквивалентнопредположению о равенстве давлений по обе стороны от неё, т.е. P₁= P₂= P.

При фазовыхпревращениях процессына границе раздела носят согласно параграфу "Статистическое обоснование второго начала термодинамики: формула Больцмана для статистической энтропии" из раздела 4.2 "Физическая термодинамика" статистическийхарактер.

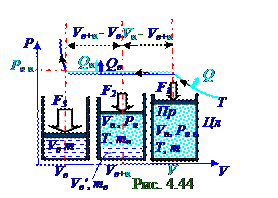
На (рис.44)границе раздела водаи пар, происходит постоянный процесс перехода молекул из водыв пар и обратно. В равновесномсостоянии они взаимно компенсируются. Изотермическое при T температуре сжатие водяногопара, что сопровождается отводом Q_п теплоты, приводит при V = V_п объёме к образованию в Цл цилиндре под Пр поршнем, к которому приложен вектор F₁ внешней силы, насыщенного пара воды mмассой с P_н _п давлением. В состоянии, когда F модуль вектора F внешней силы достиг F₂значения, что сопровождается отводом Q_п, Q_в теплоты, часть насыщенного пара водыпревращается в воду m_в массой, которая занимает V_в' объём, а оставшаяся часть насыщенного пара водыm_п массой с P_н _п давлением занимает V_п' объём. В состоянии, когда F модуль вектора F внешней силы достигает F₃значения, весь насыщенный парпревращается в воду m массой, которая занимает V_в объём. Двухфазному равновесному состоянию вода + пар соответствует горизонтальный участок изотермы.

Удельные(4.2) из раздела 4.1 "Физическая термодинамика"объемыv_0п, v_0всоответственно насыщенного параи водыимеют следующий вид: v_0п = V_п/m; v_0в= V_в/m, (4.414) где (рис. 4.44) V_п - объёмнасыщенного пара воды, когда весьпарm массой в Цл цилиндре под Пр поршнем при значении F модуля вектора F внешней силы, равном F₁, превратился из ненасыщенного в насыщенноесостояние; V_в- объёмводы m массой, образовавшейся из всего насыщенного парав Цл цилиндре под Пр поршнем при

значении F модуля вектора F внешней силы, равном F₃.

При значении F модуля вектора F внешней силы, равном F₂, под Пр поршнем в Цл цилиндре при P_н _п давлении насыщенного пара водыm_в масса водыимеет с учётом (4.414) следующее значение: m_в= V_в'/v_0в ↔ V_в' = m_вv_0в↔ V_в' = m_вV_в/m, (4.415) где V_в'- объёмводыm_в массой, образовавшейся из насыщенного парав Цл цилиндре под Пр поршнем при значении F модуля вектора F внешней силы, равном F₂.

При значении F модуля вектора F внешней силы, равном F₂, под Пр поршнем в Цл цилиндре

m_п масса насыщенного пара воды при P_н _п давленииимеет с учётом (4. 414) следующее значение: m_п= V_п'/v_0п ↔ V_п' = m_пv_0п↔ V_п' = m_пV_п/m, (4.416) где V_п'- объёмнасыщенного пара водыm_п массойв Цл цилиндре под Пр поршнем при значении

F модуля вектора F внешней силы, равном F₂.

Сумма (4.410) V_в' объёмаводыm_в массой и (4.416) V_п' объёманасыщенного пара воды

m_п массойв Цл цилиндре под Пр поршнем равняется (рис.4.44) следующему значению суммарногоV_в₊_п

объёма насыщенный пар - вода на горизонтальном участке изотермы при значении F модуля вектора F внешней силы, равном F₂:

V_в₊_п = V_в' + V_п' = (m_вV_в/m) + (m_пV_п/m) ↔ V_в₊_п = [m_вV_в/(m_в+ m_п )] + [m_пV_п/(m_в+ m_п )] ↔

↔ V_в₊_п = (m_вV_в + m_пV_п)/(m_в+ m_п ) ↔ V_в₊_п = m_п[V_п+ (m_в/m_п)V_е]/m_п[1 + (m_в/m_п)] ↔

↔ V_в₊_п = [V_п+ (m_в/m_п)V_е]/[1 + (m_в/m_п)] ↔ V_в₊_п + [(m_в/m_п)V_в₊_п] = [V_п+ (m_в/m_п)V_е] ↔

↔ [(m_в/m_п)V_в₊_п] - [(m_в/m_п)V_е] = V_п - V_в₊_п ↔ m_в/m_п = (V_п - V_в₊_п) /(V_в₊_п - V_в), (4.417)

где m = m_в+ m_п - масса насыщенного пара воды в Цл цилиндре под Пр поршнем при значении

F модуля вектора F внешней силы, равном F₁, из которой на горизонтальном участке изотермы образовалась m_в массаводыи осталась m_п масса насыщенного пара воды; с другой стороны m - масса воды, которая образовалась в Цл цилиндре под Пр поршнем при значении F модуля вектора F внешней силы, равном F₃, из всего насыщенного пара.

Согласно (4.417) в равновесном двухфазномсостоянии вода - пар, которому (рис.4.44) соответствует горизонтальный участок изотермы сжатия водяногопара при T температуре, отношение m_в/m_п массы m_вводык m_п массе насыщенного пара воды численно равно отношению длины отрезка V_п - V_в+_п, который представляет собой разностьмежду V_побъёмом всегонасыщенного пара воды исуммарнымV_в+_п объёмом насыщенный пар - вода, к длине отрезка V_в+_п - V_в, который представляет собой разностьмежду суммарнымV_в+_п объёмом насыщенный пар - вода и V_в объёмом воды, полученной из всего насыщенного пара.

Выражение (4.412) применимо для расчёта отношений масс вещества, находящемся в равновесном двухфазномсостоянии, и имеет следующий вид: m_I/m_II = (V_II- V_I₊_II)/(V_I₊_II - V_I), (4.418) где m_I, m_II - массы вещества, находящемся в равновесном двухфазномсостоянии, например, m_I - масса кристалла, а m_II - масса жидкости, полученная при плавлении части кристалла; V_I - объём 1-ой фазы, когда, например, вся жидкостьпревратилась в кристалл; V_II - объём 2-ой фазы, когда, например, весь кристаллпревратился в жидкость; V_I₊_II- суммарный объём, занимаемый 1-ой и 2-ой фазой, например,кристалломи жидкостьюв равновесном двухфазномсостоянии.

Анализ равновесного двухфазного состояния вещества с помощью термодинамического потенциала Гиббса

Термодинамический G(P, T) потенциал Гиббса (4. 200) из раздела 4.1 "Физическая термодинамика"термодинамической системы при постоянных P давлении и T температуре, находящейся вравновесном двухфазномсостоянии с M₁, M₂массами фаз, имеет следующий вид: G(P, T) = M₁(t)φ₁(P, T) + M₂(t)φ₂(P, T), (4.419) где φ₁(P, T) = G₁(P, T)/M₁(t) , φ₂(P, T) = G₂(P, T)/M₂(t) - соответственно удельные термодинамические потенциалыГиббса 1-ой фазыс M₁(t) массой и 2-ой фазыс M₂(t) массой.

При фазовыхпревращенияхобщаяM масса 1-ой фазыс M₁(t) массой и 2-ой фазыс M₂(t) массой остаётся неизменной, т.е. не зависит от момента t времени, в который производят измерение этой общейM массы, поэтому имеет место следующее выражение: M = M₁(t) + M₂(t), (4.420) где M₁(t), M₂(t) - соответственно массы 1-ой и 2-ой фаз термодинамической системы, находящейся вравновесном двухфазномсостоянии, в произвольный момент t времени.

Если M₁(t) масса 1-ой фазы термодинамической системы, находящейся при постоянных

P давлении и T температуре вравновесном двухфазномсостоянии, в момент t_i времени измерения этой M₁(t_i) массы уменьшилась на ΔM величину по сравнению с M₁(t_i-1) массой в предшествующий момент t_i-1 времени, то согласно (4.415) на такую же ΔM величину увеличилась M₂(t) масса 2-ой фазы в момент t_i времени измерения этой M₂(t_i) массы по сравнению с M₂(t_i-1) массой в предшествующий момент t_i-1 времени, поэтому термодинамический G(P, T) потенциал Гиббса в данный момент

t_i времени имеет следующий вид: G(P, T) = [M₁(t_i) - ΔM]φ₁(P, T) + [M₂(t_i) + ΔM]φ₂(P, T). (4.421)

Исследование (4.421) функции G(P, T) = G термодинамического потенциала Гиббса на минимум в данный момент t_i времени по независимой переменной M₁(t_i) = M₁массой 1-ой фазы термодинамической системы, находящейся при постоянных P давлении и T температуре вравновесном двухфазномсостоянии с (4.420) M₂(t_i) = M - M₁(t_i) = M - M₁ массой 2- ой фазыэтой термодинамической системы, приводит к следующему выражению:

∂G/∂M₁ = ∂[(M₁ - ΔM)φ₁+ (M - M₁)φ₂]/∂M₁= (φ₁∂M₁/∂M₁) - (φ₂∂M₁/∂M₁) = 0 ↔ φ₁(P, T) = φ₂(P, T), (4.422) где M - общая масса вещества в термодинамической системе, находящейся при постоянных

P давлении и T температуре вравновесном двухфазномсостоянии, является для этой термодинамической системы величиной постоянной; ΔM = M₁(t_i) - M₁(t_i-1) - приращение M₁(t_i) массы 1-ой фазы термодинамической системы, находящейся при постоянных P давлении и T температуре вравновесном двухфазномсостоянии, которое в данный момент t_i временипостоянно;

φ₁= φ₁(P, T) = G₁(P, T)/M₁(t_i), φ₂= φ₂(P, T) = G₂(P, T)/M₂(t_i) - соответственно удельные термодинамические потенциалыГиббса 1-ой фазыс M₁(t_i) массой и 2-ой фазыс M₂(t_i) массой в термодинамической системе, находящейся при постоянных P давлении и T температуре вравновесном двухфазномсостоянии, которые в данный момент t_i временипостоянны.

Согласно (4.422) минимум термодинамического потенциала Гиббса у двухфазной термодинамической системы, находящейся при постоянных P давлении и T температуре, свидетельствует о равновесномсостоянии этой термодинамической системы, которое сопровождается равенствомв данный момент t_i времени φ₁(P, T), φ₂(P, T) удельных термодинамических потенциаловГиббса 1-ой и 2-ой фаз.

Уравнение P давленияв зависимости от T температурына границе раздела

2-ух фаз термодинамической системы, находящейся в данный момент t_i времени вравновесном двухфазномсостоянии, может быть получено из решения (4.422) φ₁(P, T) = φ₂(P, T) выражения относительно P давленияв f функции от T температуры, т.е. P = f(T). Например, этим P = f(T) уравнением является (рис. 4.44) горизонтальный участок изотермы на границе раздела

насыщенный пар - вода, а также этим P = f(T) уравнением является (рис. 4.46) кривая плавленияна границе раздела жидкость - твёрдое тело.

Фазовые переходы первого рода в двухфазной термодинамической системе: уравнение Клапейрона - Клаузиуса

Равенствов данный момент t_i времени (4.422) φ₁(P, T) = φ₂(P, T), т.е.φ₁= φ₂, удельных термодинамических потенциаловГиббса на границе раздела 1-ой и 2-ой фаз в термодинамической системе, находящейся вравновесном двухфазномсостоянии, но различиеих следующих первых производных по независимымP давлению и T температуре свидетельствует о фазовом переходе первого рода: (∂φ₁/∂T)_P ≠ (∂φ₂/∂T)_P; (∂φ₁/∂P)_T ≠ (∂φ₂/∂P)_T, (4.423) где индексы _"_P_", _"_T_" при первых производных означают, что при определении частной производной по независимойT температуре постояннымпараметромявляется P давление, а при определении частной производной по независимомуP давлению постояннымпараметромявляется T температура.

Характерной особенностью фазовых переходов первого рода является поглощениеили выделениетеплоты при их осуществлении. К фазовым переходам первого родаотносятся превращения при испарении, конденсации, плавлениии кристаллизациивещества.

Цикл (рис.4.19) из раздела 4. 1 "Физическая термодинамика" Карно включает

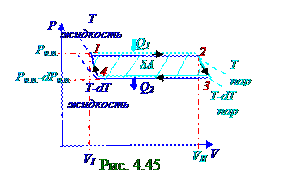
(рис. 4.45) горизонтальные 1-2, 3-4 участки изотермы, в пределах которых происходит постоянный равновесныйпроцесс перехода молекул из жидкостив насыщенный пар и обратнопо (4.422) фазовому переходу первого рода, и две 2-3, 4-1 адиабаты.

В результате изотермического1-2 процесса от нагревателяс T температурой происходит передача рабочему телуQ₁теплоты, в результате чего из 1- го состояния жидкость, т.е. 1-ая фаза,

m массой V_I объёмом испаряется и превращается в насыщенный парP_н.п_. давлением. В результате изотермического 1-2 процесса во 2- ом состоянии вся жидкость в результате равновесногоизотермического расширения при T температуре и P_н.п_. давлении 2-ух фаз термодинамической системы жидкость- насыщенный пар переходит в фазовое состояние насыщенный пар m массой

V_II объёмом.

В результате 2-3 процесса происходит (4.68) из раздела 4. 1 "Физическая термодинамика" адиабатическое расширение насыщенного пара, сопровождающееся уменьшением его температуры от T до T-dT значения иуменьшением его давления от P_н.п до P_н.п.- dP_н.п значения.

В результате изотермического3-4 процесса холодильникус T-dT температурой передаётся от рабочего телаQ₂ теплота, в результате чего из 3- го состояния насыщенный пар, т.е. 2 -ая фаза, m массой V_II объёмом конденсируется и превращается в жидкостьP_н.п.- dP_н.п давлением. В результате изотермического 3-4 процесса во 4 - ом состоянии весь насыщенный пар в результате равновесногоизотермического сжатия при T-dT температуре и

P_н.п.-P_н.п давлении 2-ух фаз термодинамической системы насыщенный пар - жидкость переходит в фазовое состояние m массой V_I объёмом.

В результате 4-1 процесса происходит (4.68) из раздела 4. 1 "Физическая термодинамика" адиабатическое сжатие жидкости, сопровождающееся увеличением его температуры от T-dT до

T значения иувеличением его давления от P_н.п.- dP_н.п до P_н.п значения.

КПД (4.123) из раздела 4.1 "Физическая термодинамика" (рис. 4.45) тепловой машины вциклическом процессе имеет следующий вид: η = δA/Q₁, (4.424)

где δA - работа, выполненная рабочим телом - насыщенным паром в циклическом процессе при его переходе из 1- го в 3- ье состояние и затем возвращения из 3- го в 1- ое состояние, численно равна заштрихованной площади между горизонтальными 1-2, 3-4 участками изотермы и 2-3, 4-1 адиабатами. Эта заштрихованная площадь, вследствие (рис. 4.45) малости приращения dT, dP_н.п соответственно температуры и давлении 2-ух фаз термодинамической системы жидкость- насыщенный пар между 2 - мя горизонтальными 1-2, 3-4 участками изотермы, приблизительноравна площади заштрихованногопрямоугольника, поэтому δA работа, выполненная рабочим телом - насыщенным паром в циклическом процессе имеет следующий вид: δA = P(V_II - V_I ) - (P -dP)(V_II - V_I ) ↔ ↔ δA = dP(V_II - V_I ) = dP(mv₀_II - mv₀_I) = m(v₀_II - v₀_I)dP, (4.425) где dP - малое приращение давления в термодинамической системе, находящейся вравновесном двухфазномсостоянии; V_II - объёмнасыщенного пара m массой, который вследствие (рис.4.45) малости приращения dT, dP_н.п соответственно температуры и давлении 2-ух фаз термодинамической системы жидкость- насыщенный пар между 2 - мя горизонтальными 1-2, 3-4 участками изотермы, приблизительно одинаков в 2, 3 состояниях на 2-3 адиабате; V_I - объёмжидкости m массой в

12 3 4 5 6 Следующая ⇒