Лекция 17 3 страница

Ионные кристаллы. В (рис. 4.50) узлах кристаллическойрешёткипомещаются ионыразных знаков. Силы взаимодействия между этими ионамиявляются в основном электростатическими, т.е. (5.1) из раздела 5.1 «Электростатика» кулоновскими силами. Связь, обусловленная электростатическимисилами притяжения между разноименно заряженными ионами,

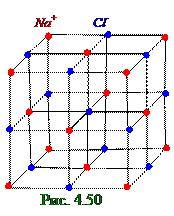
называетсягетерополярнойили ионной. Типичным примером ионнойрешётки служит (рис.4.50) решётка каменной NaCl соли, принадлежащей к (рис. 4.48, е) кубической кристаллической решётке. Ближайшими соседями положительных являются отрицательные ионы. В газообразномсостоянии NaCl состоит из молекул, в которых объединяются попарно положительные Na⁺ ионы натрия и отрицательные Cl^-ионыхлора. Образующая молекулу группировка из положительных Na⁺ ионов натрия и отрицательных Cl^-ионовхлора утрачивает в (рис. 4.50) кристалле обособленное существование, превращаясь в пределах этого кристалла в однугигантскуюмолекулу.

Атомные кристаллы. В узлах кристаллической решёткипомещаются нейтральные атомы. Связь, объединяющая в кристалле, а также и в молекуле нейтральные атомы, называется гомеополярныйили ковалентной. Силы взаимодействия при гомеополярной связи имеют также электрический, но не кулоновский, характер. Объяснение этих сил может быть дано только на основе квантовой механики.

Гомеополярная связь осуществляется электронными парами. Это означает, что в обеспечении связи между двумя атомами участвует по одному электронуот каждого атома. По этой причине гомеополярная связь имеет направленныйхарактер. При гетерополярной связи (рис. 4.50) каждый ион воздействует на все достаточно близкие к нему ионы. При гомеополярной связи воздействие направлено на тот атом, с которым у данного атома совместная электронная пара.Гомеополярная связь может осуществляться только валентными, т.е. наименее связанными с атомом, электронами. Поскольку каждый электронможет обеспечить связь только с одним атомом, число связей, в которых может участвовать данный атомссоседними атомами, равно его валентности.

Типичным примером атомных кристаллов служит алмаз, атомы в центре тетраэдра C углерода (рис.4.51) которого окружены четырьмя соседними атомами, находящихся в вершинах 1, 2,3,4 правильного тетраэдра. Каждый атом имеет четыре валентныхсвязи, изображённых на рис. 4.51 красными штриховыми линиями c соседними C атомами углерода. Зелёными линиями на рис. 4.51 изображены воображаемые ребра

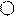
правильного тетраэдра. Согласно структуре атомного кристалла каждый из четырёх валентных электроноватома C углерода входит в электронную пару, связывающий данный атом с одним из соседей.

Решётку типа алмазаимеют полупроводниковые материалы: Ge германий, Si кремний.

Металлические кристаллы. Большинство металлов имеет кристаллическиерешётки одного из трёх типов: кубическую(рис. 4.48, е) объёмноцентрированную, в которой положительные ионыэтихметаллов находятся в узлах и в центре куба, кубическую(рис. 4.48, е) гранецентрированную, в которой положительные ионыэтихметаллов находятся в узлах и в центре граней куба, а также гексагональную(рис. 4.48, д)кристаллическуюрешётку. Между положительными ионами,подобно молекулам газа, движутся электроны, отцепившиеся от атомов при образовании металлического кристалла. Эти электроны играют роль "цемента", удерживая вместе положительные ионы; в противном случае кристаллическаярешётка распалась бы под действием сил отталкиваниямежду ионами. Вместе с тем эти электроны удерживаются силами притяжения положительных ионовв пределах кристаллическойрешётки и не могут её покинуть.

Молекулярные кристаллы. Молекулярные решётки образуют, например, следующие вещества в замороженном состоянии: H₂, N₂, O₂, CO₂, H₂O. Таким образом, обычный лёд, а также так называемый сухой лёд, т.е. твёрдая углекислота, представляют собой молекулярные кристаллы. Кристаллыобычного льдаотносятся к гексагональной(рис. 4.48, д) кристаллической решётке. В узлах кристаллической решёткипомещаются молекулы. Силы связи между молекулами в молекулярных кристаллахимеют ту же природу, что и силы притяжения между молекулами, приводящие к отклонению газов от идеального состояния. По этой причине их называют согласно параграфу "Газ Ван – дер – Ваальса: уравнение, критические параметры, внутренняя энергия"из раздела 4.1 "Физическая термодинамика" ван- дер- ваальсовскимисилами.

Дефекты в кристаллах. Теплоёмкость кристаллов

Дефектами кристаллов называют нарушения идеальной (рис. 4.48), (рис. 4.49)кристаллическойструктуры. Точечные нарушения кристаллической структуры могут наступить в следующих случаях: 1) в отсутствии атома в узле решётки, т.е. в наличии вакансии; 2) в замене атома данного вещества, т.е. в замене своего атома чужим или примесныматомом; 3) во внедрении лишнего своего или чужого атома в межузельноепространство кристаллическойструктуры. Точечные дефекты кристаллической структуры вызывают нарушения правильности кристаллической решётки, распространяющиеся на расстоянии порядка нескольких размеров (рис. 4.46) элементарнойячейки. Кроме точечных дефектов кристаллической структуры, существуют дефекты, сосредоточенные вблизи некоторых линий, которые называют линейнымидефектамиили дислокациями в кристаллах.

Простейшими видами дислокаций являются (рис. 4.52) краеваяи (рис. 4.53) винтовая.

При краевой дислокациивнутри кристалла одна из изображённых на рис. 4.52 пунктирной линиейкристаллографическихплоскостей, вследствие её обрыва, отсутствует. Отсутствие внутри кристалла одной из кристаллографическихплоскостей приводит к смещению, например, правых соседних кристаллографическихплоскостей, вследствие чего справа от (рис.4.52) кристалла появляется "лишняя" кристаллографическаяплоскость по линии EF.

Контур, проведённый по траектории элементарного кристалла при его трансляции вокруг оборванной кристаллографическойплоскости, т.е. при перемещении этого элементарного кристаллапо траектории, изображённой на рис.4.52 красной линией, с последовательным

совмещением с себе подобными элементарными кристаллами,замыкаетсяпоFA линии. Вектор FA, называемый вектором Бюргерса, направлен от "лишней" кристаллографическойплоскости, появившейся вследствие обрыва одной из кристаллографическихплоскостей внутри кристалла, к соседней кристаллографическойплоскости и перпендикуляренэтот вектор Бюргерсалинии FM краевойдислокации.

У кубической(рис.4.48, е) объёмноцентрированной, кубической(рис.4.48, е) гранецентрированной, а также гексагональной(рис. 4.48, д)кристаллическойрешётке металлов легко происходит сдвиг по атомным плоскостям при наличии сдвиговых напряжений, направленных на рис. 4.52 по красной стрелке, в кристалле металла по направлению кристаллографическойплоскости с краевойдислокацией. Первоначально имевшаяся краевая дислокация, появившаяся вследствие обрыва одной из кристаллографическихплоскостей внутри кристалла и изображённая на рис.4.53 штриховыми линиями,под воздействием созданных по направлению красной стрелки сдвиговых напряженийперемещается вдоль этого кристалла. Это (рис.4.53) перемещение краевой дислокациисопровождается поочерёдным сдвигоматомов кристаллографическойплоскости, лежащей над краевой дислокацией, относительно кристаллографическойплоскости, лежащей под краевой дислокацией.

Дислокации оказывают сильное влияние на физические свойства кристаллов, в том числе и на их прочность. В частности, наличие дислокацийвреальных кристаллах служат причиной того, что пластическая деформация этих реальных кристаллов происходит под воздействием напряжений, на нескольких порядков меньших, чем вычисленные значения напряжений длякристаллов, не имеющих дислокаций.Пластической деформациейреального кристалла называется деформация, сохраняющаяся после того, как снимается напряжение, вызвавшее этупластическую деформациюреального кристалла.

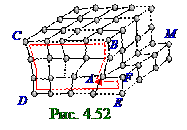
При (рис. 4.54) винтовой дислокации кристаллографическиеплоскости, лежащие, например, в горизонтальной плоскости чертежа, смещены одна относительно соседней по винтовойлинии. При (рис. 4.54) винтовой дислокациивеличинавектора FA Бюргерса определяется шагом воображаемого винта, по которому смещены кристаллографическиеплоскости, и направлен этот вектор FA Бюргерса параллельно линии винтовой дислокации, имеющей в горизонтальной плоскости чертежа на рис. 4.54 форму окружности.

Винтовая дислокация часто возникает в процессе роста кристаллов из раствора этихкристаллов или расплава. Захват атома гладкой кристаллографическойплоскостью энергетически менее выгоден и поэтому менее вероятен, чем присоединение атома к ступеньке, ориентированной (рис. 4.54) по FA линии и существующей на поверхности кристалласвинтовой дислокацией. Поэтому кристаллыпредпочитают расти со встроенной внутрь винтовой дислокацией.

Объёмтвёрдых телпри нагревании меняется мало, поэтому их (4.56) из раздела 4. 1 "Физическая термодинамика"молярная C_pтеплоемкость при постоянномP давлении незначительно отличается от (4.52) из раздела 4.1 "Физическая термодинамика"молярной C_Vтеплоемкости при постоянном V объеме, так что можно положить для твёрдого тела C_p ≈ C_V и рассчитывать молярную теплоёмкость C = 3R твердого тела (4.60) из раздела 4.1 "Физическая термодинамика"по закону Дюлонга и Пти.

Основные представления о строении жидкостей. Поверхностное натяжение и свободная поверхностная энергия

Жидкостями называются тела, которые, имея определённый объём, принимают форму сосуда, в котором они находятся. Характер теплового движения в жидкостях определяет сходство свойств жидкостей со свойствами как твёрдыхтел, так и газов. Подобно твёрдымтелам жидкости мало сжимаемы. Это свойство связано с сильным межмолекулярнымвзаимодействием частиц в жидкости. При сжатиижидкостей уменьшаются расстояния между молекулами и резко возрастают силы отталкивания, препятствующие сжатию. Жидкости имеют относительно большие плотности и так же, как твёрдыетела, сопротивляются не только сжатию, но и растяжению. Сходство свойств жидкостейи реальных газовпри высоких температурах и малых плотностях при повышении температуры проявляется в том, что уменьшаетсякоэффициент поверхностногонатяжения жидкостей и удельная теплота парообразованияэтих жидкостей, сближаются значения плотностей сухого насыщенного параи кипящей жидкости.

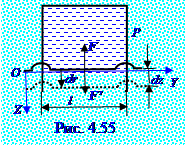
Экспериментально установлено, что поверхность жидкости под действием вектораF сил поверхностного натяжения стремится принять такую форму, чтобы иметь минимальную площадь. К подвижной невесомой перемычке (рис.4.55), находящейся на П - образной Р рамке с плёнкойжидкости, например, жидкого мыла, для предотвращения её движения вверх под действием вектораF сил поверхностного натяжениянеобходимо приложить, равный по модулюF и противоположный по направлению этому векторуF силповерхностного натяжениявектор F' внешнейсилы.

С учётом двух поверхностей плёнки, которые оказывают независимое и одинаковоевоздействие на перемычку l длиной, модуль F' вектора F' внешнейсилы имеет следующий вид:

F' = 2σl, (4.431) где σ[Н/м] - коэффициент поверхностного натяжения, численно равный силе, с которой плёнка оказывает воздействие на границу, например, на перемычку длиной 0,5 м (рис.4.45) с учётом двух поверхностей плёнки.

При медленном перемещении перемычкина dz величину площадь поверхности мыльной плёнкиувеличивается на dS_пов величину, которая с учётом одинакового увеличения двухповерхностей, находящихся в плоскости чертежа и за ней, имеет следующий вид: dS_пов= 2ldz. (4.432) Предположение о том, что процесс перемещения перемычки протекает медленно, позволяет считать его изотермическим(4.14) из раздела 4.1 "Физическая термодинамика". Элементарная δA′ работа (1.82) из раздела 1.0 "Физические основы механики", выполненная вектором F' внешнейсилы при растяжении плёнки на dy величину в направлении (рис.4.55) вектора

dr элементарного перемещения этой плёнки и совершённая против сил поверхностного натяженияс учётом (4.331), (4.332) имеет следующий вид:

δA′ =F'dr =F'dr cos(F'^dr ) = F'dz = 2σldz = σdS_пов ↔ σ = δA′/dS_пов. (4.433) Согласно (4.433) σ коэффициент поверхностного натяжениячисленно равен работе, которую необходимо затратить при изотермическом процессе увеличения на единицу площади поверхности, являющейся границей двух фаз, т.е. σ коэффициент поверхностного натяжениячисленно равен удельной свободной поверхностной энергии на границе двух фаз. Для случая (рис.4.55)

σкоэффициент поверхностного натяжениячисленно равен работе, которую необходимо затратить при изотермическом процессе увеличения каждой из площадей плёнки в плоскости чертежа и за ней на 0,5 единицы площади.

Элементарная работа (1.82) из раздела 1.0 "Физические основы механики", выполненная вектором F силы поверхностного натяжения при растяжении (рис.4.54) плёнки на dz величину с учётом противоположного направления этого вектора F силы поверхностного натяжения вектору

dr элементарного перемещения границы плёнки, имеет следующий вид: δA = Fdr =Fdr cos(F^ dr ) = - Fdz = - 2σldz = - σdS_пов, (4.434) где (4.434) dS_пов = 2ldz приращение площади поверхности мыльной плёнкипри медленном перемещении невесомой перемычки l длиной на dz величину с учётом одинакового увеличения двух поверхностей этой мыльной плёнки, находящихся в плоскости чертежа и за ней.

Элементарная δA работа, выполняемая вектором F силы поверхностного натяжениякак консервативнойсилы в потенциальном поле силповерхностного натяжения, по аналогии с (1.97) из раздела 1.0 "Физические основы механики"равна дифференциалу dW_p потенциальнойW_p энергии поверхности раздела мыльная плёнка- газ с отрицательным знаком, вследствие чего эта элементарная δA работа имеет с учётом (4.334) следующий вид:

δA_k = - dW_p ↔ - σdS_пов = - dW_p ↔ dW_p = σdS_пов, (4.435) гдедифференциал dW_p потенциальнойW_p энергии поверхности раздела мыльная плёнка- газпри положительном dS_пов приращении площади поверхности мыльной плёнкиявляется также положительной величиной, т.е. W_p потенциальная энергия поверхности раздела мыльная плёнка- газ возрастает; при отрицательном dS_пов приращении площади поверхности мыльной плёнкиявляется также отрицательной величиной, т.е. потенциальнаяW_p энергия поверхности раздела мыльная плёнка- газ убывает.

Равновесие смачивающей и несмачивающей капель жидкости на поверхности твердого тела

Капля с фронтальным (рис. 4.56) видом 2 несмачивающей жидкости на поверхности 3 твёрдого тела, окружённых 1 газом, имеет сферическуюформу сθкраевымуглом. В случае 2 несмачивающей жидкости θкраевой угол, измеренный между плоскостью 3 твёрдого тела и касательнойк сферической поверхности 2 жидкости внутри этой жидкости имеет величину π/2 < θ < π.

На dl элементарный участок контура 2 несмачивающей жидкости (рис. 4.57) на поверхности

3 твёрдого тела, имеющий форму окружности с l₁ = 2πR₁ длиной, действуют три вектора dF₂₁, dF₁₃ и dF₂₃силы.

Вектор dF₂₁ силы (4.436) поверхностного натяжения, действующий на dl элементарный участок контура (рис. 4.57) и направленный (рис. 4.56) по касательнойк сферической поверхности в сторону уменьшения площади раздела 2 несмачивающей жидкости-1 газа, имеет следующий вид: dF₂₁ = - nσ₂₁dl, (4.436)

где n - вектор единичной (рис. 4.57) внешней нормали к границе раздела трёх сред

1 газ - 2 жидкость - 3 твёрдое тело направлен в случае 2 несмачивающей жидкостиповерхности

3 твёрдого телав противоположную вектору dF₂₁ силы поверхностного натяжениясторону, поэтому в (4.336) присутствует "-" знак; σ₂₁ - коэффициент поверхностного натяженияна границе сферической поверхности раздела 2 жидкость-1 газ.

Вектор dF₁₃ силы поверхностного натяжения, действующий на dl элементарный участок контура (рис. 4.56) и направленный по касательнойк плоской поверхности в сторону уменьшения площади раздела 1 газа-3 твёрдое тело, имеет следующий вид: dF₁₃ = - nσ₁₃dl, (4.437)

где σ₁₃ - коэффициент поверхностного натяженияна границе плоской поверхности раздела 1 газа-3 твёрдое тело; n - вектор единичной внешней нормали к границе раздела трёх сред 1 газ - 2 жидкость - 3 твёрдое тело направлен в случае (рис.4. 56) 2 несмачивающей жидкости поверхности

3 твёрдого тела ив случае (рис. 4.58) 2 смачивающей жидкостиповерхности

3 твёрдого тела в противоположную вектору dF₁₃ силы поверхностного натяжениясторону, поэтому в (4.437) присутствует "-" знак.

Вектор dF₂₃силы поверхностного натяжения, действующий на dl элементарный участок

(рис. 56) и направленный по касательнойк плоской поверхности в сторону уменьшения площади раздела 2 жидкости - 3 твёрдое тело, имеет следующий вид: dF₂₃ = nσ₂₃dl, (4.438) где σ₂₃ - коэффициент поверхностного натяженияна границе плоской поверхности раздела

2 жидкости - 3 твёрдое тело; n - вектор единичной внешней нормали к границе раздела трёх сред 1 газ - 2 жидкость - 3 твёрдое тело направлен в случае (рис.4. 57) 2 несмачивающей жидкости

поверхности 3 твёрдого тела ив случае (рис.4.58) 2 смачивающей жидкостиповерхности

3 твёрдого тела водинаковуюс вектором dF₁₃ силы поверхностного натяжениясторону, поэтому в (4.438) присутствует "+" знак.

Случай механического равновесияdl элементарного участка для капли жидкости, несмачивающей (рис. 4.56), (рис.4. 57) поверхность твёрдого телас краевым углом

π/2 < θ < π и смачивающей (рис.4. 58), (рис.4. 59) поверхность твёрдого телас θ < π/2 краевым углом, описывается следующим уравнением статики: dF₂₁+ dF₁₃ + dF₂₃= 0. (4.439) Проекция выражения (4.439) на n внешнююнормаль к 1 газ - 2 жидкость - 3 твёрдое тело границе раздела трёхсред, которым для случая (рис.4. 57) 2 жидкости, несмачивающейповерхность

3 твёрдого тела, является l₁контур, а для случая (рис.4. 59) 2 жидкости, смачивающейповерхность

3 твёрдого тела, является l₂контур, имеет следующий вид: dF₂₁cosθ - dF₁₃ + dF₂₃= 0, (4.440)

⇐ Предыдущая 1 234 5 6 Следующая ⇒