Контакты

Случайная статья

Пример 2.. Решение.. Арифметический способ. Алгебраический способ. Геометрический способ

⇐ ПредыдущаяСтр 3 из 6Следующая ⇒

Пример 2.

а) Решите уравнение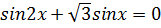

б) Найдите все корни этого уравнения, принадлежащие отрезку .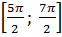

Решение.

Решая уравнение, получаем или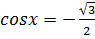

Из уравнения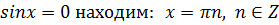

Из уравнения 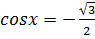находим: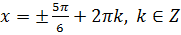

Отметим, что решение уравнения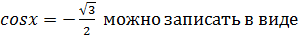

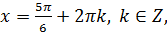
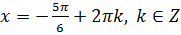
б) Рассмотрим отбор корней на отрезке .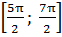

1. Арифметический способ

Пусть 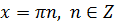. Подставляя n=… 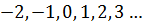, получаем 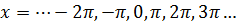. Отрезку 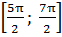принадлежит корень .

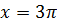Пусть 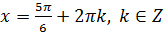.Подставляя k=… получаем 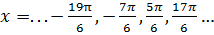. Отрезку 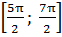принадлежит только .

Пусть 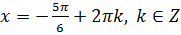.Подставляя k =… 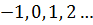получаем 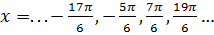. Отрезку 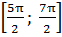принадлежит только .

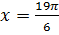Отрезку 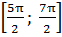принадлежат корни: .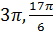

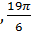2. Алгебраический способ

Отберем корни, принадлежащие отрезку 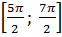. Решаем двойное неравенство.

Пусть .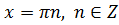

Тогда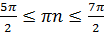

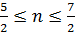
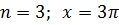
Пусть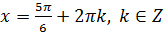

Тогда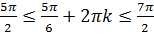

.

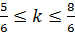
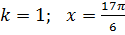Пусть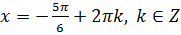

Тогда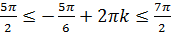

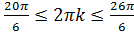
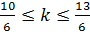
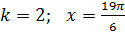
Отрезку 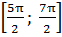принадлежат корни: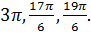

3. Геометрический способ

1. Корни уравнения изображается точкой А, а корни уравнения 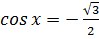- точками В и С, отрезок 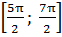изображен жирной дугой (см. рис.). В указанном отрезке содержаться три корня уравнения .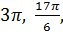

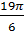у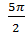

0

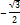
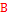
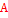х

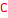
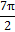
2. Корни, принадлежащие отрезку 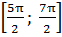, отберем по графику у=sinx. Прямая y=0 (ось 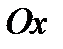) пересекает график в точке 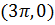, абсцисса которой принадлежит отрезку 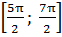, равна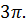

у

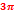
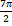
Х

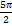
Корни, принадлежащие отрезку 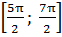, отберем по графику у=сosx. Прямая y= 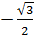пересекает график в двух точках, абсцисса которых принадлежат отрезку 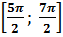, Так как период функции 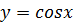равен 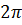, то эти абсциссы равны 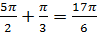и .

у

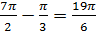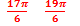
Х

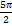
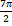
В отрезке 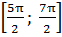содержится три корня: .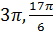

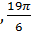3. Рассмотрим отбор корней с помощью координатной прямой.

у=sinx ////////////////////////////////////////

у=сosx /////////////////////////////////////

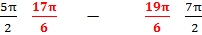
Ответ.

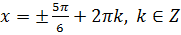
б) .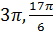

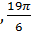⇐ Предыдущая 1 234 5 6 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.