Задача 17.

Задача 17.

Имеется универсальное множество чисел.

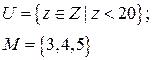
А) Найти мажоранты и миноранты для множества .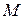

К мажорантам относятся элементы

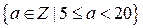К минорантам относятся элементы множества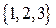

Супремум 5, он же является максимумом.

Б) На множестве всех рациональных чисел, больших пяти, не существует минимума, однако существует инфимум 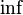такого множества, который равен пяти. Инфимум не является минимумом, так как пять не принадлежит этому множеству. Если же определить множество всех натуральных чисел, больших пяти, то у такого множества есть минимум и он равен шести. Вообще говоря, у любого непустого подмножества множества натуральных чисел существует минимум.

Для множества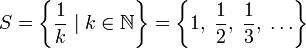

; .

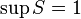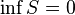Пусть E множество на числовой прямой и с-число ( ).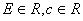

1. Число с называется мажорантой множества E если для всех x из E . ( )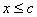

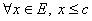2. Число с называется минорантой множества E если для всех x из E . ( )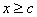

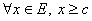Пример:

E=(-3;5)

(-4) – миноранта

(-3) – миноранта

(5) – мажоранта

(6) - мажоранта

Определение:

1. Мажоранта принадлежащая множеству называется его наибольшим элементом (Max)

2. Миноранта принадлежащая множеству называется его наименьшим элементом (Min)

Определение:

1. Наименьшая мажоранта множества называется его точной верхней гранью. (Супремум, Sup E).

2. Наибольшая миноранта множества называется его точной нижней гранью. (Инфинум, Inf E).

Пример:

Sup (E)=5

Inf (E)=-3

Определение:

1. Множество E называется ограниченным сверху если у него есть хотя бы одна мажоранта.

2. Множество E называется ограниченным снизу если у него есть хотя бы одна миноранта.

Теорема:

1. Любое не пустое ограниченное сверху множество имеет точную верхнюю грань.

2. Любое не пустое ограниченное снизу множество имеет точную нижнюю грань.

Доказательство:

1. Пусть X не пустое ограниченное сверху множество. Обозначим через Y множество мажорант для множества X. Проверим, что для этих двух множеств выполнены условия аксиомы полноты. Действительно, X 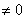, по условию, поскольку X ограничено сверху, значит есть хотя бы одна мажоранта, значит и Y не пустое.

Y расположено правее чем X т.к. элементы Y это мажоранты для X. Значит по аксиоме полноты найдется точка с лежащая между этими двумя множествами.

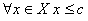-мажоранта для X

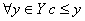- наименьшая мажоранта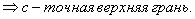

Профессор В. Наумов

⇐ Предыдущая 1 2 3 4 56