
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Отношения. Задача 1
2. Отношения
Задача 1
А) A= {1, 2, 3}; B= {1, 2, 3, 4, 5, 6}.
Множество A × B содержит18 упорядоченных пар.
Выделим на этом множестве отношение «больше»: a> b, где a ∈ A и b ∈ B, тогда
R= {(2, 1), (3, 1), (3, 2)}, т. е. из18 пар множества A × B три упорядоченные пары принадлежат отношению a R b, где R обозначает слово «больше». Если вместо букв подставить их значения, то получим верные утверждения: 2 > 1; 3 > 1; 3 > 2.
Б) Найдем сечение отношения по 3.
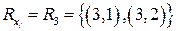 . Множество всех сечений отношения
. Множество всех сечений отношения  называется фактор-множеством множества
называется фактор-множеством множества 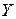 по отношению к
по отношению к  .
.
Фактор-множество можно обозначать списком
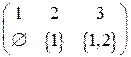 .
.
В) Найдите |R|, если R определено следующим образом: x делит y(без остатка); x∈A; y∈B, где A= {1, 2, 3, 4, 5}; B = {6, 7, 8, 9, 10, 11, 12}.
Г) Найдите |R|, если R определено следующим образом:
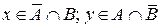 xAB ∈ I ; yAB ∈ I ,
xAB ∈ I ; yAB ∈ I ,
где A= {1, 2, 3, 4, 5}; B = {3, 4, 5, 6, 7, 8, 9, 10}.
Показать, то отношение modp является отношением эквивалентности
Пусть n=pq+r.
Говорят, что число x сравнимо с y по модулю p, если (x-y)=mp. Записывают xºy(modp).
Покажем, что это отношение эквивалетности при p>1.
1. Рефлексивность 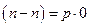 .
.
2. Симметричность 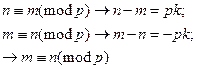
3. Транзитивность
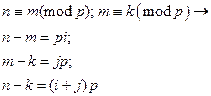
Задача 1а).Построить родословное дерево, в котором использовать обозначения:
= - брак;
Дереву принадлежат только прямые потомки.
Дети короткой вертикальной линией соединяются с горизонтальной линией, ведущей к родителям.
Пусть дерево имеет вид
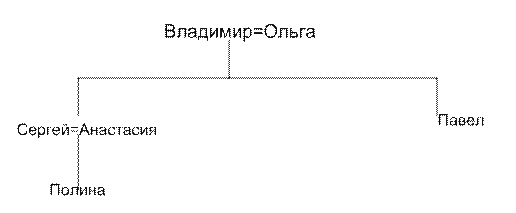
Построить отношения «быть родственником», «быть потомком», «быть предком».
Привести примеры унарных, бинарных и тернарных отношений.
«Быть целым»
«Быть равным»
«Быть отцом и матерью»

Задача 2.Бинарное отношение задано матрицей.
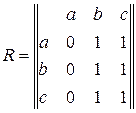 .
.
Проверить выполнение свойств симметричности, рефлексивности, транзитивности. Отношение обладает свойством транзитивности.

Задача 3.В множестве 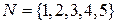 заданы отношения:
заданы отношения:
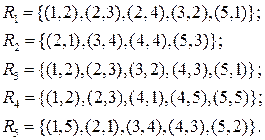
Задать отношения другими способами.
Задача 4Функция f:R→R>0, f(x)=ex , устанавливает взаимно однозначное соответствие множества всех действительных чисел R с множеством положительных действительных чисел R>0. Обратным к отображению f является отображение g:R>0→R, g(x)=ln x.
2) Отображение f:R→R≥0, f(x)=x2, множества всех действительных R на множество неотрицательных чисел R≥0
сюръективно, но не инъективно, и поэтому не является биективным
Задача 5Пусть даны два множества A={1; 3; 5; 7}и B={2; 4; 6}. Соответствие задано следующим образом t={(x; y) | x+y=9}. Задать данное отношение как множество упорядоченных пар, орграфом, в виде матрицы.
Решение. 1) t={(3; 6), (5; 4), (7; 2)} - есть задание отношения как множества упорядоченных пар;
2) соответствующий ориентированный граф показан на рисунке.

3) в матричном представлении это соответствие имеет вид
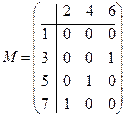 .
.

Задача 6 Пусть A={1,2,3} и B={2,3,4}. Представить графически их декартово произведение.
Тогда множество A×B состоит из следующих девяти элементов: (1,4), (2,4), (3,4), (1,3), (2,3), (3,3), (1,2), (2,2), (3,2). Графически элементы произведения множеств A×B удобно помещать на «координатной плоскости», считая, что первый множитель A расположен на горизонтальной полуоси, а второй множитель B – на вертикальной. Например,
(1,4) (2,4) (3,4)
(1,3) (2,3) (3,3)
(1,2) (2,2) (3,2)
Задача 7. Построить различные соответствия
А) Постройте граф соответствия «Больше» для множеств Х={2,4,6}и Y={1,3,5}. Найдите образ числа 4 и полный прообраз числа 5.
Б) Для множеств Х={25,16,7,6}и Y={5,2,3,9,1}задайте график соответствия «Делится на». Постройте граф этого соответствия. Найдите образ числа 6 и полный прообраз числа 2. Какой элемент имеет пустой прообраз? Для какого элемента полный прообраз совпадает со всем множеством Х? Найдите область определения и множество значений этого соответствия.
В) Пусть Х={мама, папа, рама, яма} и Y={а, м, р, п, ф, я}. Задайте график соответствия «В слово х входит буква у» и постройте граф этого соответствия. Найдите образ слова «мама» и полный прообраз буквы «м». Найдите букву с пустым прообразом.
Г) Пусть Х – множество учащихся в классе, Y – множество парт в том же классе. Каждому учащемуся сопоставляется парта, за которой он сидит. Что такое полный прообраз данной парты? Что такое образ множества всех учащихся?
Д) Множество Х состоит из всех квадратов на плоскости, а множество Y – из всех окружностей на той же плоскости. Каждому квадрату х сопоставляется вписанная в него окружность. Является ли это соответствие отображением Х в Y. Инъективно ли оно? Что является полным прообразом данной окружности? Станет ли это соответствие инъективным, если заменить Х на множество Z квадратов, стороны которых параллельны осям координат?
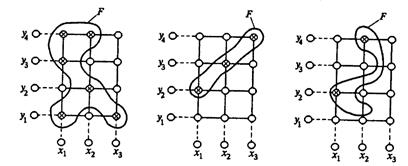
Задача 8. Пусть задано множество отношений
А)
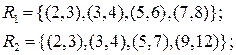
Найти
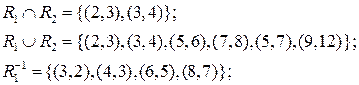
Б) Заданы множества:
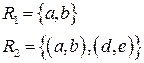
Найти декартовы произведения:
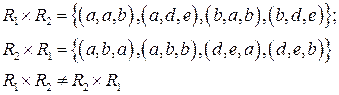
В) Конституенты. На множествах вводят алгебры, например алгебру 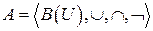 .
.
Множества 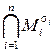 называются конституентами. Сложность конституент равна
называются конституентами. Сложность конституент равна  .
.
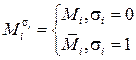
Построить конституенты для множества 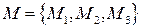
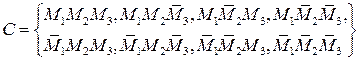
Сопоставим каждой конституенте двоичный набор, а также номер двоичного набора.
Задача. Найти степени множества
А) 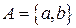
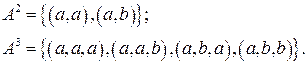
Б) 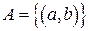
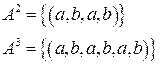
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|