Задача.. Задача 6.

⇐ ПредыдущаяСтр 2 из 6Следующая ⇒

Задача.

Проверить теорему де-Моргана на примете, если универсум состоит из цифр от 1 до 9. A={3,4,5,6}, B={2,5,6,9}.

Задача 6.

Перечислите множество всех подмножеств (булеан), если исходное множество

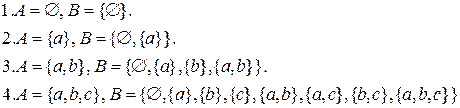
A<-set()

2^A

A<-set("a","b","c")

2^A

Задача 7. Даны три множества А, В, С. С помощью диаграммы Эйлера показать

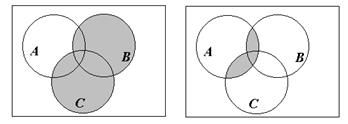С помощью диаграмм Эйлера – Венна проиллюстрировать справедливость соотношения

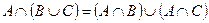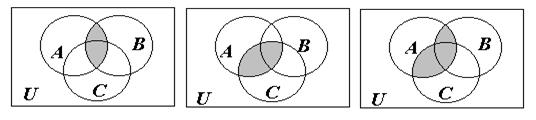Используя определения операций над множествами, доказать данное тождество теории множеств. Проиллюстрировать доказательство с помощью диаграмм Венна.

Задача 8. Докажите с помощью тождественных преобразований:

А)

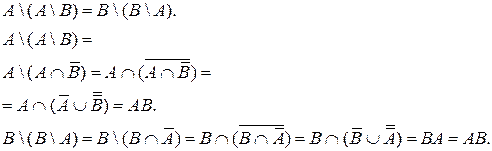
Б)

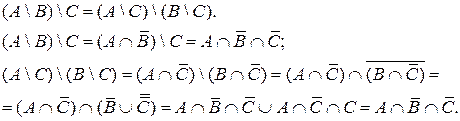
Подтвердить данные выводы диаграммами Эйлера.

В)

Доказать следующее тождество .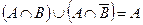

Докажем это тождество двумя способами: аналитически (используя равносильности алгебры множеств) и конструктивно (используя диаграммы Эйлера-Венна).

1. С помощью отношения дистрибутивности получим

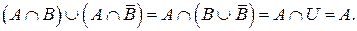
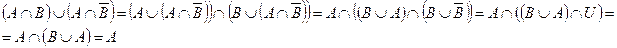
2. Построим соответствующие диаграммы Эйлера-Венна.

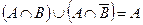
Задача 9. Определите пересечение множеств через разность

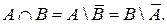
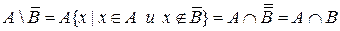
Задача 10. В каком отношении находятся множества А и В, если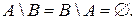

Для доказательства будем использовать два тождества.

Тождество

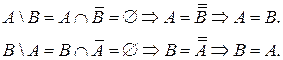
Задача 11. Докажите, что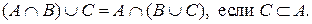

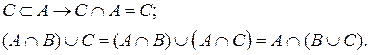
Проверим справедливость данного тождества также с помощью диаграмм Эйлера.

Упростите выражения

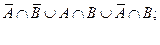
Задача 12. Покажите справедливость тождеств

А)

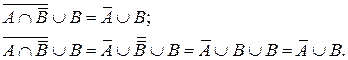
Б)

В)

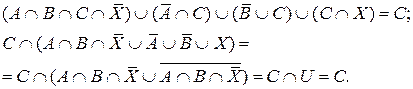
Задача 13. Исходя из определения дизъюнктивной суммы 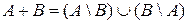покажите ее свойства:

А) коммутативность

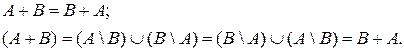
Б) ассоциативность

Задача 14. С помощью диаграммы Венна решить уравнение

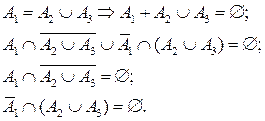
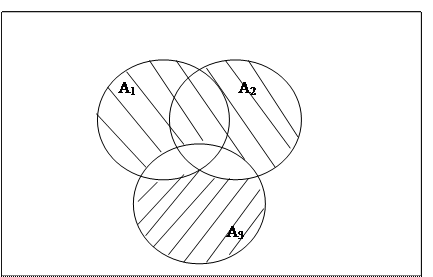
Решение задачи сводится к выделению штриховкой тех областей, которые входят в А₁ и не входят в объединение А₂, А₃, а также тех областей, которые входят в объединение А₂, А₃, и не входят в А₁. Оставшаяся незаштрихованная область образует универсум.

Как видно, решением будет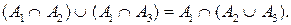

Задача 15. Решить систему:

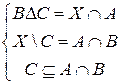Построим множества так, чтобы .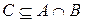

Будем говорить, что множества 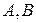находятся в общем положении, если . Построим так, чтобы Х и С находились в общем положении, исходя из второго соотношения.

Получим множества

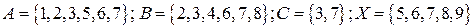Из первого равенства найдем

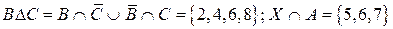Так как данные два множества равны между собой, то множества 2,4,5,7, 8 – пустые. Следовательно, получаем

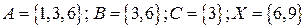Из второго уравнения получим

. Так как эти множества равны между собой, то множества 3, 9 – пустые. Получим

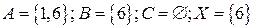Видим, что .

Проверим равенства системы.

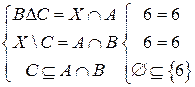
Ответ

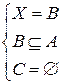
Задача Мощность множеств

пусть A — множество всех натуральных чисел, делящихся без остатка на 50, B — множество всех четных натуральных чисел. Эквивалентны ли эти множества?

Представим множества A и B в виде (еще раз напомним: число 0 не является натуральным):

A={50, 100, 150, 200, 250}.

B={2, 4, 6, 8, 10}

По этим записям видно, что множество A составляет часть элементов множества B, т. е. является его подмножеством: A ⊂ B. Но с другой стороны, если числа —элементы множеств A и B — записать в порядке возрастания, то эквивалентность множеств устанавливается очень легко, так как между их элементами хорошо просматривается взаимно однозначное соответствие:

Элементу 2 ∈ B соответствует элемент 50 ∈ A, элементу 4 ∈ B соответствует элемент 100 ∈ A и т. д. Следовательно, множества A и B эквивалентны. Говоря языком конечных множеств, четных натуральных чисел столько же, сколько натуральных чисел, делящихся без остатка на 50. Таким образом, положение «часть меньше целого», справедливое для конечных множеств, в случае бесконечных множеств перестает быть безусловно верным.

⇐ Предыдущая 123 4 5 6 Следующая ⇒