
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача 13
Задача 13
А) Разместить в лексикографическом порядке двоичные векторы (0,0,0,1),(1,0,1,0), (1,1,0,0), (0,1,1,1).
Б) Записать десятичные числа от 0 до 9 в двоичном коде и расположить их в лексикографическом порядке.
Задача 14.Пусть A={1; 2; 3; 4; 5; 6}. На этом множестве задано отношение rÍA2, которое имеет вид: r={(1, 1), (2, 2), (3, 3), (4; 4), (5; 5), (6; 6), (1; 2), (1; 4), (2; 1), (2;4), (3;5), (5; 3), (4; 1), (4; 2)}. Какими свойствами обладает данное отношение?
Решение. 1) Это отношение рефлексивно, так как для каждого aÎA, (a; a)Îr.
2) Отношение не является антирефлексивным, так как не выполняется условие этого свойства. Например, (2, 2)Îr, но отсюда не следует, что 2¹2. (Отношение называется антирефлексивным, если 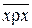 .)
.)
3) Рассмотрим все возможные случаи, показав, что отношение r является симметричным: (Отношение r на множестве Х называется симметричным, если для любых х, уÎХ из хrу следует уrх. 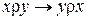 .)
.)
| Случай | (a, b)Îr | (b, a) | (b, a)Îr? |
| (1; 2) | (2; 1) | Да | |
| (1; 4) | (4; 1) | Да | |
| (2; 1) | (1; 2) | Да | |
| … | … | … | … |
4) Данное отношение не является антисимметричным, поскольку (1, 2)Îr и (2,1)Îr, но отсюда не следует, что 1=2.
5) Можно показать, что отношение r транзитивно, используя метод прямого перебора.
| Случай | (a, b)Îr | (b, c)Îr | (a, c) | (a, c)Îr? |
| (1; 2) | (2; 1) | (1; 1) | Да | |
| (1; 2) | (2; 2) | (1; 2) | Да | |
| (1; 2) | (2; 4) | (1; 4) | Да | |
| (1; 4) | (4; 1) | (1; 1) | Да | |
| (1; 4) | (4; 2) | (1; 2) | Да | |
| … | … | … | … | … |
Задача 15.
А) Укажите транзитивные отношения:
1) равно; 5) меньше на 5;
2) больше или равно; 6) быть южнее;
3) не равно; 7) быть врагом;
4) быть другом; 8) быть логарифмом.
Отношение называется интранзитивным, если из aRb и bRc следует, что утверждение aRc является ложным. Примером может служить отношение «больше на 4». Если «a на 4 больше b» и «b на 4 больше c», то утверждение «a на 4 больше c» ложно.
Какие из приведенных отношений являются интранзитивными?
Б) Укажите, какие из отношений являются рефлексивными и симметричными:
1) точка a удалена от точки b на4 см;
2) по количеству жителей город A равен городу B;
3) дробь a равна дроби b в множестве дробей;
4) число a делится на b без остатка в множестве целых положительных чисел;
5) площадь фигуры a равна площади фигуры b в множестве геометрических фигур на плоскости;
6) числа a и b при делении на 5 дают одинаковые остатки;
7) a– b ≠0, где a, b ∈{3, 4, 5, 6, 7}; a– b
В) Укажите отношения эквивалентности:
1) быть попутчиком в одном вагоне пассажирского поезда;
2) a + b = 100, где a, b ∈ {1, 2, …, 100};
3) a = b, где a, b ∈ {1, 4, 8, 9};
4) прямая a перпендикулярна прямой b;
5) треугольник a подобен треугольнику b;
6) Сидоров живет двумя этажами выше Михайлова;
7) a сердит на b.
8) Подобие в множестве всех треугольников на плоскости.
9) Принадлежность к одной группе факультета.
Г) Построить граф и матрицу отношения эквивалентности для разбиения на классы эквивалентности 
Д) Отношение сравнимо с числом 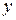 по модулю является отношением эквивалентности. Покажите , что это так и приведите примеры такого отношения.
по модулю является отношением эквивалентности. Покажите , что это так и приведите примеры такого отношения.
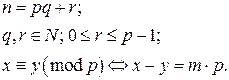
Данное отношение является отношением эквивалентности при 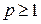 .
.
Приведите примеры
Пусть 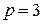 .
. 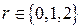 .
.
Классы эквивалентности
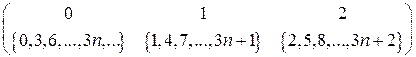 .
.
Перечислим классы эквивалентности для модуля 2,6.
Задача 16 Построить диаграмму Хассе для множества двоичных векторов длины 3, частично упорядоченное по правилу: V<W, если в векторе W единицы стоят на всех тех местах, на которых они стоят в V (и, может быть, еще на некоторых).
а) Указанное отношение частичного упорядочения приводит к тому, что имеются сравнимые и несравнимые векторы, например, (010) < (011), но (010) и (100) несравнимы.
б) Выпишем все множества векторов {(000), (001), (010), (011), (100), (101), (110), (111)}.
в) Разместим несравнимые векторы по ярусам и соединим точки, помечающие сравнимые векторы, стрелками. Тогда получим фигуру, которая в алгебре логики называется единичным кубом. Здесь верхняя грань двух произвольных элементов A и B - это элемент, в который есть путь из A и из B; нижняя грань A и B - это элемент, из которого есть путь и в A и в B.
Г) построим диаграмму Хассе. Пусть дано универсальное множество 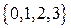 . Подмножество на универсуме: иметь нечетное число членов.
. Подмножество на универсуме: иметь нечетное число членов.
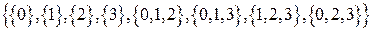 . Построить диаграмму Хассе, если отношение частичного порядка
. Построить диаграмму Хассе, если отношение частичного порядка 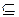 .
.
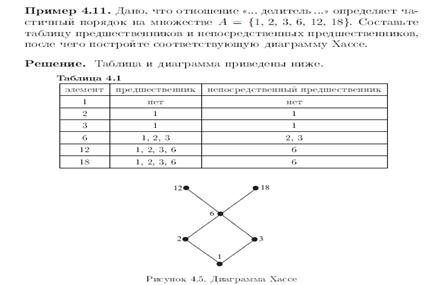
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|