
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическое занятие на тему: Множества, отношения, функции
Практическое занятие на тему: Множества, отношения, функции
1. Множества
Задача 1. В каких соотношениях находятся между собой множества:
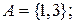
В – множество нечетных чисел;
С- множество решений уравнения 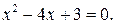
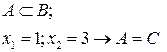
Задача 2.
А) Запишите множество перечислением его элементов
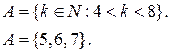
library(sets) > #Задание множества
#Creation and manipulation of sets.
> ## constructor
s1<- set(5, 6, 7)
A<- set(5, 6, 7)
set(1,2,3) - set(1,2)set_intersection(set(1,2,3), set(2,3,4), set(3,4,5))set_union(set(1,2,3), set(2,3,4), set(3,4,5))set_symdiff(set(1,2,3), set(2,3,4), set(3,4,5))
Б) Задать множества 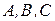 перечислением их элементов и найти
перечислением их элементов и найти 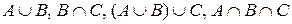 , если:
, если:
1)  – множество делителей числа 12;
– множество делителей числа 12;  – множество корней уравнения
– множество корней уравнения 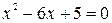 ;
; 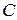 – множество нечетных чисел
– множество нечетных чисел 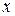 таких, что
таких, что 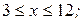
A<- set(-12,-6,-4,-3,-2,-1,1,2, 3,4,6,12)
B<- set(5,1)
C<- set(3,5,7,9,11)
set_union(A,B)
A|B
2) 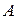 – множество четных чисел
– множество четных чисел 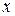 таких, что
таких, что 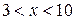 ;
; 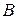 – множество делителей числа 21;
– множество делителей числа 21; 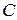 – множество простых чисел, меньших 12.
– множество простых чисел, меньших 12.
В) Найти 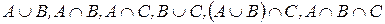 и изобразить эти множества на числовой прямой, если:
и изобразить эти множества на числовой прямой, если:
1) 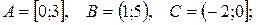
2) 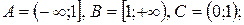
3) 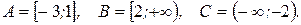
Г) Пусть 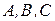 – такие множества, что
– такие множества, что 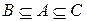 . Найдите множество
. Найдите множество 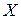 , удовлетворяющее условиям
, удовлетворяющее условиям 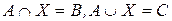 .
.

Приведите пример квадратного уравнения, множество действительных корней которого пустое.
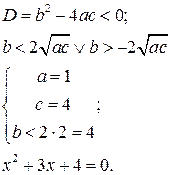
Д) Даны множества: A = {1, 2, 3}; B = {2, 3, 4}; I = {1, 2, 3, 4, 5, 6}.
Найдите элементы множеств: 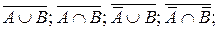
Задача 3.
А) ## cardinalitys <- set(1, list(1, 2))length(s)lengths(s)
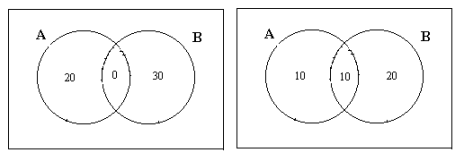
Б) Лекции по экономике посещают 20 студентов, по математике - 30. Найти число студентов, посещающих лекции по экономике или математике, если 1) лекции проходят в одно и то же время, 2) лекции проходят в разные часы и 10 студентов слушают оба курса.
Очевидно, в первом случае имеем дело с непересекающимися множествами, т.к. студентов, посещающих оба курса, не существует, т.е. А∩В=Æ, если А - множество студентов, посещающих лекции по математике, В - по экономике. Следовательно, n(А∩В)=0, а n(А∪В)= n(А)+n(В)=20+30=50.
Во втором случае, число студентов, посещающих лекции только по математике, - 10, т.к. из 20 человек 10 слушают оба курса. Аналогично только экономику слушают 20 человек из общего числа студентов, равного 30. Следовательно, лекции по математике или экономике слушают 40 человек или n(А∪В)= n(А)+ n(В)- n(А∩В). Графическое решение задачи приведено на рисунке.
Эта формула - простейший вариант формулы включений и исключений, отвечающая на вопрос о сумме любого числа пересекающихся множеств n(А1∪А2∪... Аk). Так для k=3 получим n(А∪В∪С)= n(А)+ n(В)+ n(С) - n(А∩В) - n(А∩С) - n(В∩С) - n(А∩В∩С)
Б) A1= {1, 2, 3, 4}; B= {a, b, c}; C= {x, y, z, v, w},
Найти мощность исходных множеств, а также декартовых произведений.
тогда |A|= 4, |B|= 3, |C|= 5 и |A × B × С|= 4 ⋅3 ⋅5 = 60, т. е. множество A × B × C содержит 60 упорядоченных троек(1, a, x), (1, a, y), (1, a, z) и так далее до(4, c, w).
Задача 4. Приняв множество первых 20 натуральных чисел за универсум, запишите следующие его подмножества: А – четных чисел; В- нечетных чисел; С- квадратов чисел; D – простых чисел. В каком соотношении находятся данные множества? Запишите результат операций над данными множествами перечислением их элементов:
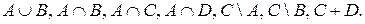
Задача 5. Даны множества
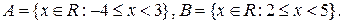
Найти
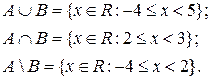
## intersection
reals(2,4) & reals(3,5)
interval(2,5,"()")|interval(1,3)
interval(1,5, "[)")
interval(1,5, "()")
#Дополнение [-Inf, 1) U (5, Inf]
!reals(1,5)
X<-set(1,2)
Y<-set(2,4)
cset_union(X, Y)
(A<-reals(-4,3))
(B<-reals(2,5))
A|B
(A<-reals(-4,3))
(B<-reals(2,5))
A&B
Индикатор, или характеристическая функция, или индикаторная функция подмножества  — это функция, определённая на множестве
— это функция, определённая на множестве 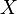 , которая указывает на принадлежность элемента
, которая указывает на принадлежность элемента 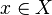 подмножеству
подмножеству 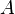 .
.
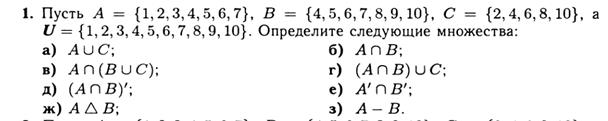
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|