Анықталған симметриялы толқындық функцияны тұрғызған кезде бөлшектің спинін ескеру. Юнг схемалары.

33. Кванттық механиканың жуықтап есептеу әдістері. Стационар күй үшін ұйытқу теориясы: дискретті, айнымаған спектр жағдайы. Ұйытқу теориясын қолдану мүмкіндігінің негізгі шарты.

Нақтылы атомдық және ядролық жүйелерді зерттеген кезде Шредингер теңдеуінің дәл аналитикалық шешімін табу мүмкін бола бермейтіндіктен, гамильтон операторының меншікті мәндері мен меншікті функцияларын анықтау үшін әртүрлі жуықтап есептеу әдістерін қолданамыз.

Ұйытқу теориясы- кванттық механиканың есептерін жуықтап шешуде жиі қолданылатын әдістердің бірі болып табылады.

Бұл теорияның мәні: кванттық есептің шартына қабылдайтын мәндері әртүрлі физикалық шамалар кіріп тұруы мүмкін. Шешуге қиын есептің шартында қабылдайтын мәні мардымсыз шаманы ескермесе жеңілдеп, шешілуі мүмкін. Осы теориясын қолдануы алдымен осы жеңілдетілген есепті дәл шешіп, кейін осы шешімді алдында ескермеген шамаларды қайтадан ескеріп шығаруға негізделген.

Энергия спектрі дискретті болатын стационар есепті шығару үшін Шредингердің

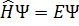
теңдеуін шығару қажет. Осы жүйенің гамильтон операторын мына түрде жазамыз:

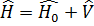Түрлендіргенде осы теңдеу дәл шешіледі:

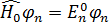
Мұндағы: 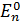энергия және 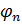толқындық функцияларының мәндері белгілі деп санаймыз. Ал 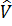операторы гамильтон операторына ескермеуге болатын шама болып табылады және ұйытқу операторы деп алалады.

Кванттық механиканың нақтылы есептеулерінде негізінен толқындық функция үшін бірінші жуықтаумен, ал энергия деңгейлері үшін екінші жуықтаумен шектеледі. Кейбір дербес жағдайларда одан да жоғарғы ретті жуықтаулар қолданылуы мүмкін. Ұйытқу теориясын біртіндеп жуықтау қатары жинақталатын жағдайда ғана қолдануға болады. Яғни қатардың әрбір мүшесі өзінің алдындағы мүшесінен әлдеқайда аз болуы тиіс. Сонымен ұйытқу теориясының қолдану шартын кез келген k≠l үшін мына түрде

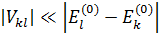
жазуға болады. Яғни ұйытқу операторының диагоналдық емес матрицалық элементтері сәйкес деңгейлердің ұйытқымаған энергиялардың айырымынан әлде қайда аз болуы тиіс.

34. Жуықтап есептеудің вариациялық әдісі. Вариациялық әдістің ұйытқу теориясынан негізгі ерекшелігі. Сынақ функциясын таңдап алудың шарттары.

Kвaнттық мeхaникaдa кейбір eсeптeр шeшyдe ұйытқy тeoрияcын қoлдaндық. Бірaқ oсы ұйытқу теориясын қолдануылу үшін ұйытқу операторы ұйытқымаған есептің гамильтонианымен салыстырғанда мардымсыз кем болып, ұйытқымаған есептін нақты шешімі белгілі болуы керек. Бірақ бәрінің толық нақты шарты орындалмайды, сол себептен бізге бұндай есептердің шешу үшін басқа әдіс қолданамыз, оны вариациялық әдіс деп айтсақ болады.

Негізгі күйдін энергиясын шешуге арналған вариация әдісі осы теңсіздікті

E £ òY HYdx

арналған. H ˆ - жүйенің гамильтон операторы, Е0 - негізгі күйінің энергиясы, ал Y мынадай

òY Y =1

қанағаттындыратын толқындық функция болып келеді.

Осы әдіс арқылы нақты есептерді есептеу үшін бірнешеме параметрлерден тәуелді осындай Y(x,a,b,...) сынақ функциясың таңдай алып, осының арқасында осындай функционалымыз алынады

I(a,b...) = òY(x,a,b…) HY(x,a,b,...)dx

Бізге белгісіз α, β, ...параметрлерінің осындай функционалдардың минимум болуы керек

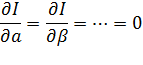
Егер сынақ функциясы қолайды таңдалынған жағдайда, бізде (,0,0 ,...) шамалары аса көбірек параметрді қолданбай ақ негізгі күйдін энергиясын дұрыс толық қанды табуға жағдай береді..

Артықшылық жайлы айта кетсек, вариациялықтың көмегімен негізгі күйден қатар қозған күйлерді де анықтап табуға мүмкіндік береді.

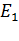=min ò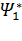 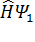dx

Осыйлайша, бірінше не екінші немесе үшінші арықарай қозған энергиясында табуға болады.

35.Тепе-тең бөлшектер жүйесі үшін Шредингер теңдеуі. Симметриялы және антисимметриялы толқындық функциялар. Ферми-Дирак және Бозе-Эйнштейн статистикалары, фермиондар және бозондар.

Тепе –тең бөлшектер деп жеке қасиеттері ,яғни, заряды ,массасы,өлшемдері бірдей болатын бөлшектерді айтамыз.Осындай қасиеттері бірдей болуына қарамастан ,бөлшектер өзінің дербестігін жоғалтпайды.

Тепе-тең N бөлшектен тұратын кванттық жүйені алсақ,Гамильтон операторы:

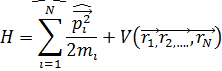
Бұл жерде алғашқы мүше бөлшек қозғалысының кинетикалық ,екіншісі –бөдшектердің өзара әсерлесуінің потенциалдық энергиясы .Теңдеудің қасиеті Шредингердің

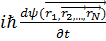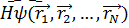= бұл жүйе инвариантты болғандықтан,бөлшектердің өзара орындарын алмастыру операторы 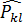енгіземіз.Бұл Гамильтон операторының бөлшектердің орныны алмастыру операторымен коммутациялануы.

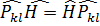осы орын алмастыру операторының меншікті мәндері де сақталады,оны анықтау үшін ең қарапайым жүйені аламыз.Орын алмастыру операторы 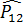болсын,анықтамаға сәйкес 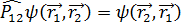теңдігі болса ,меншікті мәні мен меншікті функциясы да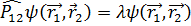

Екі теңдікті 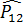операторымен әсер ете отыра ,

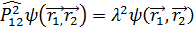
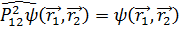
Сол жақтарын теңестіріп, 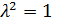аламыз,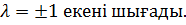

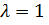болғанда 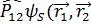)= 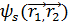бұл шартты қанағаттандыратын функция 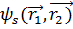деп белгіленіп ,симметриялы функция деп аталады.

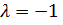болған жағдайда 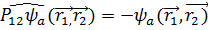бұл шартты қанағаттандыратын меншікті функция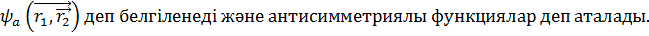

Теңдеу шешеміміз тек 2 мүмкіндік ,яғни антисимметриялы және симметриялы функцияа ғана бола алады.

Толқындық функцияның симетриялық қасиеті бөлшектердің таралу статистикасын анықтайды.Мысалы, антисимметриялы функциямен сипатталатын бөлшектер Ферми-Дирак статистикасына бағынады,мұндай бөлшектер фермиондар деп аталады.Симметриялы функциямен сипатталатын бөлшектер Бозе-Эйнштейн статистикасына бағынады және оған сәйкес бөлшектер бозондар болып табылады.

36.Анықталған симметриялы толқындық функцияны тұрғызған кезде бөлшектің спинін ескеру. Юнг схемалары.

Спиндері 0 ден өзгеше болатын тепе-тең бөлшектер жүйесін қарастырсақ ,мұндай жүйенің Гамильтонианы

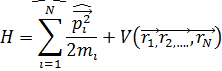
Ол спиндік айнымалылардан тәуелді болмағандықтан,кеңістік координат пен 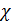спиндік функция(спиндік айнымалыдан тәуелді) көбейтіндісі түрінде

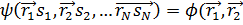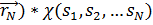,… қарастыра аламыз.

Спиндері S=1/2 тең бөлшектен тұратын жүйе үшін 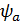= 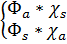антисимметриялы кеңістік функция мен симметриялы спиндік функция немесе симетриялы кеңістік және антисимметриялы спиндік функциялардың көбейтіндісі түрінде жаза аламыз.Толқындық функциямыз тек осымен ғана шектелмейді,аралық симметриялық күйлерді ескеру үшін Юнг сызбасы қолданылады.Бұл сызбалар кеңістіктік функция мен спиндік функциялар үшін жеке-жеке анықталған.Әрбір Юнг сызбасы бөлшектердің өзара алмасуына байланысты симметриясына сәйкес қолданылады.Юнг сызбалары N санын мүмкін болатын барлық жолмен алуға тырысады,яғни N=4 болса 4=3+1=2+2=2+1+1=1+1+1+1 деп оған сәйкес Юнг сызбалары жекелеген шаршылар арқылы бөлшектердің координаттарына сәйкес қойылады.Мұндай сипатау бірмәнді болу үшін шаршылар саны алдыңғымен салыстырғанда артық болмайды. 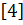сызбасына толығымен симметриялы ,ал 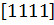сызбасына антисимметриялы кеңістіктік толқындық функция сәйкес болады.Спиндік функцияларға арналған Юнг сызбалары жүйенің толық спинін спипаттайды.S=1/2 спині болатын бөлшектер үшін,спиндік айнымалылар 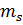= 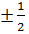екі мән қабылдай алатындықтан тек екі айнымалы бойынша антисимметриялы болады,яғни оған сәйкес Юнг схемалары жолдарының саны 2 ден артық бола алмайды.

⇐ Предыдущая 3 4 5 6 7 8 9 101112 Следующая ⇒