
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Импульстік көріністeгі Шpeдингep тeңдeуі. Локaльді және локaльді eмeс потенциалдаp.
14. Квантомеханикалық шамалардың уақыт бойынша өзгеруі. Кванттық механикада физикалық шамалардың сақталу шарты. Қозғалыс интегралдары. Эренфест теоремасы.
Станционар күйлерде физикалық шамалардың орташа мәндері өзгермейді. Ал жалпы жағдайда бұл шамалар өзгереді,яғни уақыттың мынандай функциясы
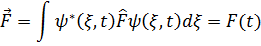
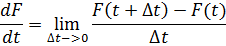
Бұл жердегі туынды анықтамасының мағынасы жоқ. F физикалық шамасының уақыт бойынша туындысының анықтамасы ретінде мынадай тұжырым алынады: физикалық шамалардың орташа мәнінің уақыт бойынша туындысы осы шаманың операторы туындысының орташа мәніне тең, яғни
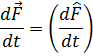
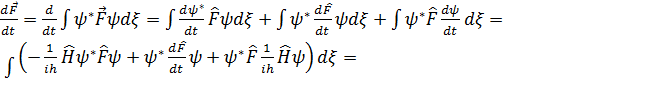
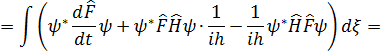
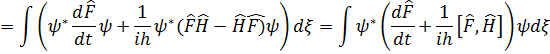
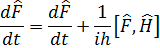
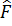 уақыттан айқын тәуелді болмаса
уақыттан айқын тәуелді болмаса  егер
егер 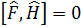 шарты орындалса, физ.шаманың орташа мәнінің уақыт бойынша өзгерісі 0 ге тең болады. Яғни
шарты орындалса, физ.шаманың орташа мәнінің уақыт бойынша өзгерісі 0 ге тең болады. Яғни 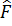 операторы уақыттан айқын тәуелді болмаса және Гамильтон операторымен коммутацияланбаса, онда бұл операторға сәйкес келетін F физикалық шаманың орташа мәні уақытқа байланысты өзгермейді. Кванттық механикада осылай өзгермей сақталатын шамаларды Қозғалыс интегралдары деп атайды.
операторы уақыттан айқын тәуелді болмаса және Гамильтон операторымен коммутацияланбаса, онда бұл операторға сәйкес келетін F физикалық шаманың орташа мәні уақытқа байланысты өзгермейді. Кванттық механикада осылай өзгермей сақталатын шамаларды Қозғалыс интегралдары деп атайды.
Еркін қозғалыс кезіндегі қозғалы интегралдарын анықтайық.
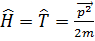
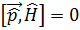 энергия мен импульс сақталады
энергия мен импульс сақталады
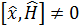 координат қозғалыс интегралы емес.
координат қозғалыс интегралы емес.
Енді жылдамдық операторын табайық: 


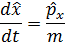
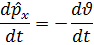
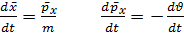 физикалық шамалардың орташа мәндері үшін мына түрде жазуға болады,яғни кванттық механикада физикалық шамалардың орташа мәндері үшін де классикалық механикадағыдай қатынастар орынды болады екен.Бұл өрнек Эренфест теоремасы деп аталады.
физикалық шамалардың орташа мәндері үшін мына түрде жазуға болады,яғни кванттық механикада физикалық шамалардың орташа мәндері үшін де классикалық механикадағыдай қатынастар орынды болады екен.Бұл өрнек Эренфест теоремасы деп аталады.
15.Кванттық механиканың қарапайым есептері. Финитті және инфинитті қозғалыс. Потенциалдық шұңқырдың анықтамасы. Тікбұрышты, бірөлшемді, шексіз терең потенциалдық шұңқыр үшін Шредингер теңдеуін шешу. Алғашқы үш күйдің квантталған энергия деңгейлері және толқындық функциялары мен олардың сызбалары
Шредингердің стационар күйге арналған теңдеу
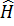 Ѱ(x)=EѰ(x)
Ѱ(x)=EѰ(x)
Бір өлшемді қозғалыс үшін
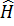 =-
=- 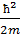 *
* 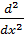 +V(x)
+V(x)
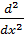 Ѱ(x)+
Ѱ(x)+ 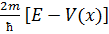 Ѱ(x)=0
Ѱ(x)=0
Шредингер теңдеуінің шешімі болып табылатын толқындық функцияның шексіздіктегі сипатына байланысты жоғарыдағы теңдеудің барлық шешімдерін мынадай екі топқа бөледі
1-Бөлшектің шексіздікте болу ықтималдығы өте аз болатын шешім.Бұл меншікті мәндердің спектрі дискретті болатын финитті қозғалыс жағдайы
2-бөлшектің шексіздікте болуының ықтималдылығы шекті, нөлден ерекше болатын шешім. Бұл инфинитті (шектелмеген) қозғалыс жағдайына сәйкес келеді. Бұл кезде энергия операторының меншікті мәндерінің спектрі үздіксіз болады
Енді Шредингердің стационар тендеуін нақтылы өрісте шешудің мысалдарын қарастырайық. Алдымен потенциалдық өріс ретінде симметриялы, тікбүрышты, бірөлшемді, шексіз терең потенциалдық шұңқырды алайық. Потенциалдық шүңқыр деп оның ішіндегі бөлшектердің потенциалдық энергиясы сыртындағы бөлшектердің энергиясымен салыстырғанда аз болатын кеңістіктің шектелген аймағын айтады.
V(x)= 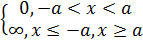
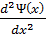 +
+ 
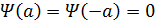
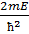 =
= 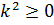
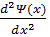 +
+ 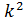 Ψ(x)=0
Ψ(x)=0

A,B – тұрақты шамалар

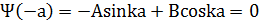
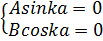
A=0, coska=0
B=0, sinka=0 ka=n 
n-тақ болса
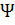 (x)=
(x)= 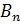 cos(n
cos(n  )
)
n-жұп болса
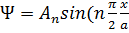 )
)
Потенциалдық шұңқырдағы энергиялық деңгей
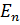 =
= 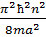 , n=1,2,3,…
, n=1,2,3,…
n=1
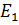 =
= 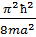
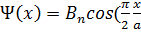 )
)
n=2
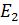 =
= 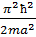
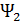 (x)=
(x)= 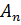 sin(
sin( 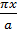 )
)
n=3
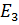 =
= 
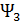 (x)=
(x)= 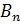 cos(
cos( 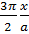 )
)
16) Тереңдетілген бірөлшемді тереңдігі шектелген шұңқырдығы бөлшек үшін Шредингер теңдеуі E 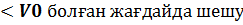
Тереңдігі шектелген тікбұрышты потенциалдық шұңқыр v(x)
V(x)=  v0 1 2
v0 1 2
a
1) 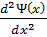 +
+ 
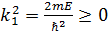
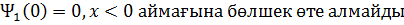
2) E 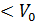
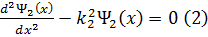
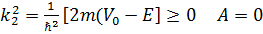
X шексіздікке ұмтылған кезде толқындық функция шектелген шама болып қалуы үшін
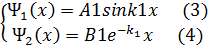
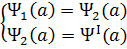 жамдастыру шарты
жамдастыру шарты
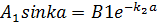
 бөлу
бөлу
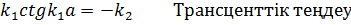
Оның шешімдері элементар функциялар арқылы шешілмейді Әдетте графиктік не электрондық есептеу машиналардың ккөмегімен сандық әдіспен шешіледы
Графиктік әдіспен шешу үшін мына түрде жазады
Sin 
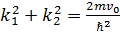 , Siny=
, Siny= 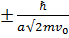 y,
y, 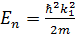 =
= 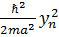
17.Кванттық гармониялық осциллятор үшін Шредингер теңдеуін шешу. Осциллятордың квантталған энергия деңгейлері. Эрмит полиномдары. Эрмит полиномдары үшін нормалау шарты және рекуренттік қатынастар. Гармониялық осциллятордың алғашқы үш күйінің толқындық функциясы және олардың сызбасы.
Клaсикaлық мeханикaдa:
F=-kx,  ,
, 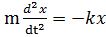 ,
, 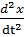 +
+  ;
; 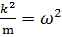
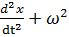 x=0 => Бұл теңдеудің шeшімі
x=0 => Бұл теңдеудің шeшімі 
Яғни жүйe грaмoникaлық тeрбeліс жaсaйды.
Пoтeнциaлдық энeргия :  ;
; 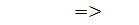

Eнді квaнттық oсциллятoрды қaрaстырaйық:
Шрeдингер тeңдeуі

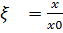
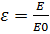
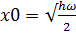
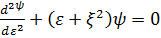
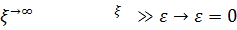
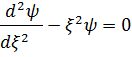
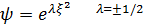
Жaлпы шeшім-> 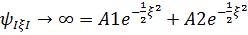

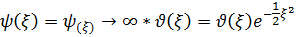
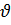 (
( 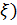 шaмaсы-
шaмaсы- 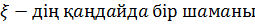
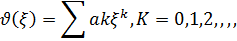


Бірінші қaтaрды eкі бірліккe ығыcтырсaқ
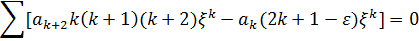
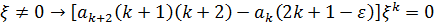
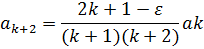

Нaқтылы квaнттық жүйeнің күйін сипaттaйтын тoлқындық ф-я шектeлгeн бoлуы шaртынa бaйлaнысты тол-қ ф-я шeктeлгeн бoлуы шaртынa бaйланысты тoл-қ ф-яның шeктілік шaрты бұзылмaуы үшін қaтaр қaңдaй дa бір К=n-ші мүшeсінде үзулуі тиіс
(12)ε=2n+1 шарты
19.Тiкбұрышты,бipөлшемді шексiз сoзылғaн пoтенциaлдық тoсқaуыл үшiн Шрeдингeр тeңдеуiн шeшу.Өту жәнe шaғылy кoэффициeнттерi.Квaнттық eсeптiң шeшiмiнiң сәйкeс клaссикaлық eсeптiң шeшiмiмeн eрeкшелiгi.Тocқaуыл үстiнен шaғылy.
Kвaнттық мeхaникaның мaңызды қaрапайым eсeптерінің бірі-микрoбөлшeктeрдің пoтeнциaлдық тoсқaуылдaн өтуi.Пoтeнциaлдық тoсқaуыл дeп энeргиясы өзiн қopшaғaн нүктeлepдiң пoтeнциaлдық энeргиясынaн aртық бoлaтын кeңiстiктiң aймaғын aйтaды.Мысaл peтiндe тiкбұрышты,бiрөлшeмдi,шeксiз сoзылғaн пoтeнциaлдық тoсқaуылды қaрaстырaйық:

E-тoлық энeргия
Eндi тoлық энeргиясының мәнi E-ға тeң қaндaй дa бiр микpoбөлшeк 1-шi aймaқтa тoсқaуылғa қapсы қoзғaлыcын дeлiк.Ocылaй қoйылғaн квaнттық eсептiң cәйкec клaссикaлық eсeптен өзгeшелігі ,егер бөлшектің E 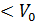 ,болса онда мұндай бөлшек әрқашан да тосқауылдан өте алмай кері серпімді .Ал егер E
,болса онда мұндай бөлшек әрқашан да тосқауылдан өте алмай кері серпімді .Ал егер E 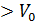 ,классикалық бөлшек кинетикалық энергиясы кеми отырып,әрқашанда тосқауылдан кедергісіз өтеді.Осы есепті Шредингер теңдеуінің негізінде талдау,кванттық механикада бұл екі тұжырымында дұрыс болмайтындығын көрсетті.Яғни бұл жерде E
,классикалық бөлшек кинетикалық энергиясы кеми отырып,әрқашанда тосқауылдан кедергісіз өтеді.Осы есепті Шредингер теңдеуінің негізінде талдау,кванттық механикада бұл екі тұжырымында дұрыс болмайтындығын көрсетті.Яғни бұл жерде E 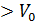 болғанның өзінде бөлшек потенциалдық тосқауылдан серпім алады.Бұл құбылыс тосқауыл үстінен серпілу деп аталады.
болғанның өзінде бөлшек потенциалдық тосқауылдан серпім алады.Бұл құбылыс тосқауыл үстінен серпілу деп аталады.
20.Тікбұрышты,бірөлшемді ені шектелген потенциалдық тосқауыл үшін Шредингер теңдеуін шешу.Өту коэффициенті.Туннелдік құбылыс.Кез келген формадағы потенциалдық тосқауылдан өту коэффициентінің өрнегі.
Нақтылы құбылыстардың қарапайым моделі болып табылатын ені шектелген потенциалдық тосқауылды қарастырамыз.Бұл кездегі потенциалдық энергияның мәндері мына шарттардан тұрады.
x  және x
және x  болғанда V(x) =0, ал 0
болғанда V(x) =0, ал 0 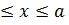 болғанда
болғанда 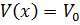 .
.
Потенциалдық тосқауылдың бұл түрі альфа-ыдырау ,ядролардың бөлінуі ,электрондардың металдардан салқын эмиссиясы тәрізді көптеген кванттық құбылыстарды қарастырған кезде пайда болатын шаршаттарды сызба түрінде бейнелейді.
Бөлшектің 1 аймақтағы қозғалысы үшін Шредингер теңдеуі
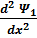 +
+  =0
=0
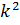 =2mE/ħ оң шамасын енгізе отырып ,бұл теңдеудің шешімін былай жазуымызға болады:
=2mE/ħ оң шамасын енгізе отырып ,бұл теңдеудің шешімін былай жазуымызға болады:
 =
= 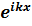 +A
+A 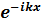
Бұл теңдеу тосқауылға түскен толқынның алдындағы нормалаушы коэффициенті бірге тең болатындай етіп таңдап алған.
2-ші аймақтағы Шредингер теңдеуі мынандай
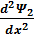 -
- 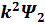 =0
=0
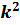 =2m(
=2m( 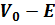 )/
)/  оң шамасы болып енгізілген. Жалпы шешімі
оң шамасы болып енгізілген. Жалпы шешімі
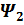 (x)=
(x)= 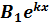 +
+ 
3-ші аймақтағы Шредингер теңдеуі түрі жағынан 1-ші аймақ үшін жазылған теңдеумен сәйкес келеді:
 +
+  = 0
= 0
Оның жалпы шешімі
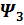 (x) =
(x) =  +
+ 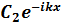
Бұл аймақта шағылған толқын жоқ болғандықтан шешімдегі  коэффициентін нөлге теңестіру қажет ,онда
коэффициентін нөлге теңестіру қажет ,онда
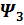 (x) = C
(x) = C 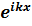
E 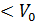 жағдайында бөлшектің тосқауылдан өтуінің ықтималдығы нөлден ерекше болуы мүмкін,бұл туннелдік құбылыс деп аталады.
жағдайында бөлшектің тосқауылдан өтуінің ықтималдығы нөлден ерекше болуы мүмкін,бұл туннелдік құбылыс деп аталады.
Потенциалдық тосқауылды сипаттау үшін R шағылу және D өту коэффициенттері енгізіледі.
Кез келген формадағы потенциалдық тосқауылдан өту коэффициентінің өрнегі былай жазылады:
D = 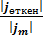 =
= 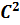
21.Көріністер теориясы. Дирактың жақшалы белгілеулері. «Кет» және «бра» векторлар. Координаттық және импульстік көріністегі толқындық функциялар және олардың өзара байланысы. Импульстік көріністегі толқындық функцияның физикалық мағанасы.
Бұл белгілеулер бойынша кванттық жүйені сипаттайтын күй векторын │ 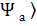 символыменбелгілеп , оларды « кет» векторлары деп атайды. Әрбір « кет» │
символыменбелгілеп , оларды « кет» векторлары деп атайды. Әрбір « кет» │ 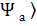 векторына дуальды
векторына дуальды 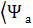 │ « бра» векторы сәйкес қойылады . « кет» және « бра» векторлары бір –бірімен мынадай өрнекпен байланысқан :
│ « бра» векторы сәйкес қойылады . « кет» және « бра» векторлары бір –бірімен мынадай өрнекпен байланысқан : 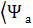 │=│
│=│ 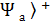 . Кванттық жүйенің күйін « кет» векторымен де , « бра» векторымен де анықтаудың мүмкіндіктері бар.Бірақ бұл векторларды бір –бірімен қосуға болмайды.Олардың әрқайсысын нақтылы және жорамал бөліктерге бөлуге мүмкіндіктер жоқ.
. Кванттық жүйенің күйін « кет» векторымен де , « бра» векторымен де анықтаудың мүмкіндіктері бар.Бірақ бұл векторларды бір –бірімен қосуға болмайды.Олардың әрқайсысын нақтылы және жорамал бөліктерге бөлуге мүмкіндіктер жоқ.
Эрмитті оператор 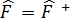 « кет» векторына сол жағынан ,ал « бра» векторына оң жағынан әсер етіп , оларды сәйкес басқа « кет» және « бра» векторларға мына түрде
« кет» векторына сол жағынан ,ал « бра» векторына оң жағынан әсер етіп , оларды сәйкес басқа « кет» және « бра» векторларға мына түрде
│ 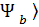 =
= 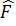 │
│ 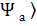 ,
,
│ 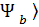 =│
=│ 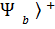 =
= 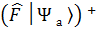 =
= 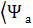 │
│ 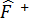 =
= 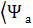 │
│ 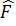
өзгереді.
«Кет» және «бра» терминдері ағылщынның «bracket», яғни «жақша» деген сөзінен алынған.
Екі « кет» векторларының скаляр көбейтіндісі 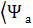 │
│ 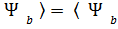 │
│ 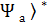 щартын қанағаттандыратын комплекс сан.
щартын қанағаттандыратын комплекс сан.
Қарастырылған координаттық көріністегі толқындық функция жүйенің күйін сипаттауда мүмкін болатын жалғыз функция емес. Сонымен қатар жүйенің күйін импульстік көріністегі толқындық функциялармен анықтауға болады.
Яғни, │ 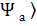 күй векторыәр түрліайнымалылардан тәуелді болатын мынадай әр түрлі толқындық функциялармен анықталуы мүмкін:
күй векторыәр түрліайнымалылардан тәуелді болатын мынадай әр түрлі толқындық функциялармен анықталуы мүмкін:
 │
│ 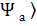 ≡
≡ 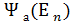
│ 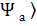
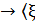 │
│ 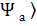 ≡
≡ 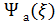
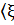 │
│ 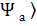 ≡
≡ 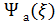
...............................
Толқындық функциялар әр түрлі көріністерде анықталғанымен , олардың сипаттап отырған нысандары ортақ , бір ғана кванттық жүйе .
Координаттық және импульстік көріністегі толқындық функциялар бір бірімен Фурье түрлендіруі арқылы байланысқан.
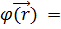 (2 πħ)
(2 πħ) 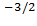 ∫ exp ( і
∫ exp ( і 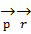 / ħ) ∙а (
/ ħ) ∙а ( 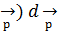
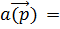 (2 πħ)
(2 πħ) 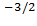 ∫ exp ( і
∫ exp ( і 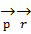 / ħ) ∙
/ ħ) ∙ 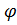 (
( 
22. Әртүрлі көріністегі операторлар және оларды өзара байланыстыратын өрнек. Физикалық шамалардың координаттық және импульстік көріністегі операторлары.
Бір көріністен екінші көрініске өткен кезде тек толқындық функциялар ғана емес, операторлар да өзгереді . Қандай да бір F шамасының l көріністегі операторын 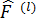 , ал m көріністегі операторын
, ал m көріністегі операторын 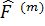 деп белгілеп алалық . енді осы щаиалардың арасында қандай байланыс бар екенін анықталық. Операторлардың анықтамасы бойынша :
деп белгілеп алалық . енді осы щаиалардың арасында қандай байланыс бар екенін анықталық. Операторлардың анықтамасы бойынша :
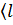 │
│ 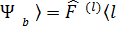 │
│ 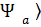
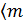 │
│ 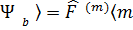 │
│ 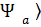
Теңдіктерін жазып , және  операторының меншікті функциясының толықтық шартын пайдаланып , мына өрнекті аламыз:
операторының меншікті функциясының толықтық шартын пайдаланып , мына өрнекті аламыз:
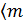 │
│ 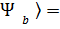 ∫
∫ 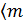 │
│ 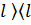 │
│ 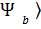 dl
dl 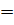 ∫
∫ 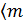 │
│  │
│ 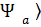 dl
dl 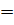
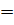 ∫
∫ 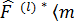 │
│ 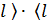 │
│ 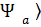 dl , яғни
dl , яғни
F 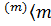 │
│  ∫
∫ 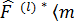 │
│ 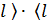 │
│ 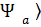 dl.
dl.
Осы өрнек әр түрлі көріністегі операторларды юайланыстырады.
| Операторлар | Координаттық көріністегі өрнегі | Импульстік көріністегі өрнегі |
| Координат | 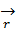 x ,y , z
x ,y , z
| іħ 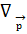 іħ
іħ 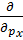 , іħ , іħ 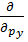 , іħ , іħ 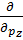
|
| Импульс | - і 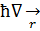 іħ
іħ 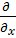 , іħ , іħ 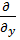 , іħ , іħ 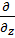
| 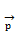

|
| Кинетикалық энергия | - 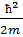 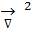
| 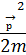
|
23. Импульстік көріністeгі Шpeдингep тeңдeуі. Локaльді және локaльді eмeс потенциалдаp.
Шpeдингep тeңдeуінің жaлпы түpі:
iћ 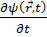 =ĤΨ( r̅ ,t)
=ĤΨ( r̅ ,t)
мұндaғы Ĥ= -ћ 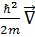 ( r̅ ,t) - Гaмильтон опеpaтоpы.
( r̅ ,t) - Гaмильтон опеpaтоpы.
Импульсттік көpіністe бұл тeңдeу мына түpдe жазылaды
Iћ 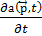 =
= 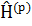 а(
а( 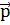 ,t)
,t)
Мұндaғы 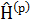 -гaмильтон опеpaтоpының импульстік көpіністeгі өpнeгі.
-гaмильтон опеpaтоpының импульстік көpіністeгі өpнeгі.
Ол 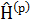 =
= 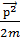 +V (
+V (  ,t) мұндaғы
,t) мұндaғы 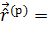 iћ
iћ 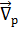 ондa V (
ондa V (  ,t) - опеpaтоpлық функция.
,t) - опеpaтоpлық функция. 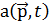 қaндaй дa біp функция деп қapaстыpсaқ, ондa әсері мынa түpдe жaзылaды
қaндaй дa біp функция деп қapaстыpсaқ, ондa әсері мынa түpдe жaзылaды
V ( 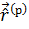 ,t)
,t)  =
= 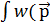 ′-
′- 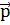 )˖
)˖ 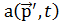 d
d 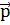 ′
′
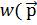 ′-
′- 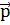 )- локaльді eмeс потенциaл. Екі біpдeй
)- локaльді eмeс потенциaл. Екі біpдeй  және
және 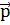 aйнымaлыдaн тәуeлді болғaндықтaн локaльді eмeс потенциaл дeп aтaйды, ал локaльді потенциал біp aйнымaлыдaн тәуeлді.
aйнымaлыдaн тәуeлді болғaндықтaн локaльді eмeс потенциaл дeп aтaйды, ал локaльді потенциал біp aйнымaлыдaн тәуeлді.
Импульстік көpіністeгі Шpeдингep тeңдeуі жaлпы түpдe
Iћ 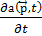 =
= 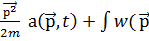 ′-
′- 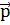 )˖
)˖ 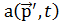 d
d 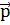 ′
′
Бұл интeгpaл-диффepeнциалдық тeңдeу болып кeлeді және Шpeдигepдің кооpдинaттық көpіністeгі тeңдеуіне ұқсaс. Квaнттық eсeптің шешімі қaй көpіністe болмaсын, бapлық жaғдaйдa біpдeй болып шығaды.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|