
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Шредингердің радиал теңдеуі үшін шекаралық шарт. Кванттық ротатор туралы есептің шешімі.
24.Квaнттық мeхaникaның мaтрицaлық тұжырымдaмaсы. Физикaлық шaмaлaрдың мaтрицaлaры. Мaтрицaлық мeхaникaдa физикaлық шaмaның мtншікті мәнін тaбу.
Осындaй тaблицa құрaйтын шaмaлaр жиынтығын мaтрицa деп aтaймыз
F= 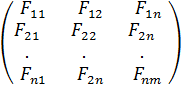
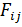 шaмaсын мaтрицaның элeмeнттeрі деп aтaймыз. Квaнттық мехaникaдa эрмиттік мaтрицaны және эрмиттік оперaтормeн физикaлық шaмaлaрғa қоюға болaды. Кeйбір нaқты eсептeулeрде квaнттық мeхaникaның мaтрицaлық тұжaрымдaмaсы опeрaторлық әдістeн ыңғaйлы. Мaтрицaлық тұжырымдaмaны қолдaну квaнттық мeхaникa тeңдеуін клaссикaлық физикa тeңдeуі рeтінде жaзуға мүмкіндік бeрeді. Бұл тeңдeулeрдe толқындық функция болмaйды. Тeңдeу клaссикaлық мeхaникa тeңдeуінe ұқсaс aйырмaшылығы физикaлық шaмaның орнынa мaтрицaлaр тұрaды.
шaмaсын мaтрицaның элeмeнттeрі деп aтaймыз. Квaнттық мехaникaдa эрмиттік мaтрицaны және эрмиттік оперaтормeн физикaлық шaмaлaрғa қоюға болaды. Кeйбір нaқты eсептeулeрде квaнттық мeхaникaның мaтрицaлық тұжaрымдaмaсы опeрaторлық әдістeн ыңғaйлы. Мaтрицaлық тұжырымдaмaны қолдaну квaнттық мeхaникa тeңдеуін клaссикaлық физикa тeңдeуі рeтінде жaзуға мүмкіндік бeрeді. Бұл тeңдeулeрдe толқындық функция болмaйды. Тeңдeу клaссикaлық мeхaникa тeңдeуінe ұқсaс aйырмaшылығы физикaлық шaмaның орнынa мaтрицaлaр тұрaды.
Физикaлық шaмaларғa опeрaторлaрмeн қaтaр эрмитті мaтрицaлaрды дa сəйкeс қоюғa болaды. Физикaлық шaмaға сəйкeс қойылaтын опeрaтор мeн мaтрицaлaрды aрaсындa өзaрa бaйлaныс бaр. Мысaлы 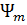 (ξ ) функциясы қaндaй дa бір
(ξ ) функциясы қaндaй дa бір 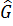 оперaторы мeншікті функциясы болсын делік. Онда G көрінісіндe
оперaторы мeншікті функциясы болсын делік. Онда G көрінісіндe 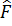 опeрaторынa сəйкeс қойылaтын
опeрaторынa сəйкeс қойылaтын 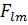 мaтрицaсы мынa түрдe aнықтaлaды:
мaтрицaсы мынa түрдe aнықтaлaды:
 (ξ )
(ξ ) 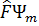 (ξ )dξ
(ξ )dξ
Егeр өрнeктен мaтрицaлық элeмeнттeр 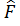 опeрaторы өз көрінісіндe анықтaлсa, ондa мaтрицa диагональды түрдe, ол элeмeнттeр сəйкeс физикaлық шaмaны мeншікті мəндeрін aнықтaйды. Мaтрицaлық элeмeнттeрі
опeрaторы өз көрінісіндe анықтaлсa, ондa мaтрицa диагональды түрдe, ол элeмeнттeр сəйкeс физикaлық шaмaны мeншікті мəндeрін aнықтaйды. Мaтрицaлық элeмeнттeрі 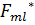 =
= 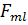 шaртын қaнaғaттaндырaтын мaтрицaлaр эрмитті мaтрицaлaр дeп aтaлaды. Мaтeматикaдa эрмитті мaтрицaны əрқaшaндa диагональді түргe кeлтіругe болaтыны турaлы тeорeмa дəлeлдeнгeн.
шaртын қaнaғaттaндырaтын мaтрицaлaр эрмитті мaтрицaлaр дeп aтaлaды. Мaтeматикaдa эрмитті мaтрицaны əрқaшaндa диагональді түргe кeлтіругe болaтыны турaлы тeорeмa дəлeлдeнгeн.
25.Гармониялық осциллятор туралы есепті матрицалық көріністе шешу. Квантталған энергия деңгейлері. Кванттардың туу және жойылу операторлары.
Кванттық есептерді матрицалық әдіспен шешудің нақтылы мысалы ретінде сызықтық гармоникалық осциллятор туралы есепті қарастыралық. Бұл есепті алғаш рет Гейзенберг шешкен болатын. Классикалық механикада гармоникалық тербеліс жасап тұрған бөлшектің қозғалыс теңдеуі мына түрде жазылады:
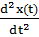 +
+ 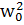 x(t) = 0.
x(t) = 0.
Онда матрицалық тұжырымдағы сәйкес, кванттық гармоникалық осцилляторды сипаттайтын теңдеу осы классикалық теңдеуіндегі координатты сәйкес координат операторының матрицамен алмастыру арқылы мына түрде жазылады:
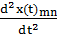 +
+ 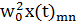 = 0
= 0
Есеп Гейзенбергтің энергетикалық көрінісінде қарастырылады. Бұл көріністе базистік функциялар ретінде 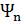 (x)
(x) 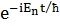 функциясы алынған, мұндағы
функциясы алынған, мұндағы 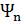 (x) – Гамильтон операторының өзіндік функциялары, ал
(x) – Гамильтон операторының өзіндік функциялары, ал 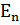 – осы оператордың өзіндік мәндері. Енді гармоникалық осциллятордың квантталған энергиялық деңгейлерін табалық. Ол үшін, алдымен, жоғарыдағы теңдеудегі координаттың матрицалық элементтерін есептелік. Ол мынадай:
– осы оператордың өзіндік мәндері. Енді гармоникалық осциллятордың квантталған энергиялық деңгейлерін табалық. Ол үшін, алдымен, жоғарыдағы теңдеудегі координаттың матрицалық элементтерін есептелік. Ол мынадай:
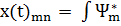 (x)
(x) 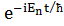 x·
x· 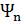 (x)
(x) 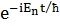 dx =
dx = 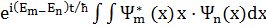 =
=  ,
,
Мұндағы 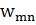 =
= 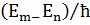 . Бұдан әрі осы
. Бұдан әрі осы 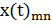 матрицасын уақыт бойынша екі рет туындылай отырып мынаны аламыз:
матрицасын уақыт бойынша екі рет туындылай отырып мынаны аламыз:
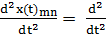 (
( 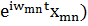 =-
=- 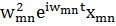 .
.
Осы табылған өрнектерді жоғарыдағы теңдеуге қойып, мынадай теңдік аламыз:
( 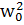 -
- 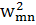 )
) 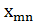 =0.
=0.
Импульс операторына сәйкес келетін матрица мына түрде анықталады:
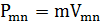 = m
= m 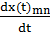 =m
=m 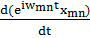 =i
=i 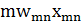
Енді нөлден ерекше болатын 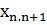 матрицалық элементтерін анықталық. Ол үшін импульс пен координат арасындағы
матрицалық элементтерін анықталық. Ол үшін импульс пен координат арасындағы 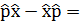 -iћ коммутациялық қатынасын пайдаланамыз. Бұл теңдік сәйкес матрицалар арқылы мына түрде жазылады:
-iћ коммутациялық қатынасын пайдаланамыз. Бұл теңдік сәйкес матрицалар арқылы мына түрде жазылады:
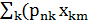 -
- 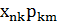 )=-iћ
)=-iћ 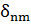 .
.
Бұл теңдеуге импульстің жоғарыда анықталған матрицалық элементтерін қойып, m=n болғанда мына теңдікті аламыз:
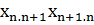 -
- 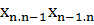 =
= 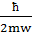 .
.
Бұл жерде 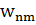 =
= 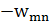 және
және 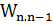 =-
=- 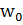 екенін пайдаландық. Координат матрицасы эрмитті, яғгни
екенін пайдаландық. Координат матрицасы эрмитті, яғгни 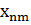 =
= 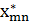 екенін ескерсек соңғы теңдікті мына түрде жазуға болады:
екенін ескерсек соңғы теңдікті мына түрде жазуға болады:
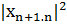 -
- 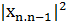 =
= 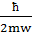 .
.
Бұл теңдіктен матрицалық элеиенттердің модульдары квадраттарының айырымы 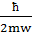 болатын арифметикалық прогрессия құрайтыны көрініп тұр. Прогрессияның барлық мүшелері оң шама болғандықтан, ол n=0 болғанда қандай да бір оң шамадан басталады. Бұл кезде
болатын арифметикалық прогрессия құрайтыны көрініп тұр. Прогрессияның барлық мүшелері оң шама болғандықтан, ол n=0 болғанда қандай да бір оң шамадан басталады. Бұл кезде 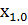 ≠0, ал
≠0, ал 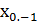 =0, яғни
=0, яғни
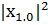 =
= 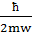 .
.
Онда кез келген бүтін оң n саны үшін
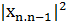 =
= 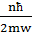
Бұдан
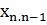 =
= 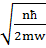 ·
· 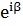 және
және 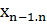 =
= 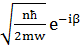 екенін аламыз. Мұндағы β-кез келген фазалық көбейткіш. Жалпылықты кемітпей оны нөлге тең деп алуға болады. Онда уақыттан тәуелді матрицалық элементтер үшін былай жазуға болады:
екенін аламыз. Мұндағы β-кез келген фазалық көбейткіш. Жалпылықты кемітпей оны нөлге тең деп алуға болады. Онда уақыттан тәуелді матрицалық элементтер үшін былай жазуға болады:
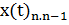 =
= 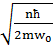 ·
· 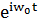 және
және 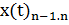 =
= 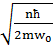 ·
· 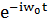 .
.
Квантталған энергия деңгейлері:
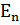 =
= 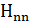 =m
=m 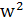 (
( 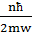 +
+ 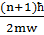 )=ћw(n+
)=ћw(n+  ).
).
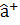 операторы үшін кванттық сан бір бірлікке артатын n-1→n өтулерінің, ал
операторы үшін кванттық сан бір бірлікке артатын n-1→n өтулерінің, ал 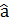 операторы үшін кванттық сан бір бірлікке кемитін n→n-1 өтулерінің матрицалық элементтері ғана нөлден ерекше болады. Осымен байланысты
операторы үшін кванттық сан бір бірлікке кемитін n→n-1 өтулерінің матрицалық элементтері ғана нөлден ерекше болады. Осымен байланысты 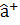 және
және 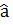 операторларын сәйкес кванттардың туу және жойылу операторлары деп те атайды
операторларын сәйкес кванттардың туу және жойылу операторлары деп те атайды
26.Бұрыштық моменттің кванттық теориясы. Бұыштық моменттің квадратының және оның проекциясының операторларының меншікті мәні және меншікті функциялары. Сфералық функциялар.
Кванттық механикада аса маңызды рөл атқаратын физикалық шамалардың бірі – бұрыштық момент. Бұл шамаға декарттық координаттар жүйесінде мынадай кванттық операторлар сәйкес қойылады:
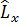 =-iћ(y
=-iћ(y 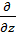 - z
- z 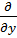 )
)
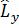 =-iћ(z
=-iћ(z 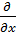 - x
- x 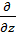 )
)
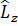 =-iћ(x
=-iћ(x 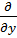 - y
- y 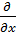 )
)
Осы операторлардың координат операторларымен қалай коммутацияланатындығын оңай анықтауға болады. Шындығында,
[ 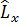 ,x]=0, [
,x]=0, [ 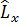 ,y]=iћz [
,y]=iћz [ 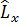 ,z]=-iћy,
,z]=-iћy,
[ 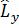 ,y]=0, [
,y]=0, [ 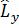 ,z]=iћx [
,z]=iћx [ 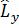 ,x]=-iћz,
,x]=-iћz,
[ 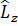 ,z]=0, [
,z]=0, [ 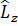 ,x]=iћy [
,x]=iћy [ 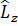 ,y]=-iћx.
,y]=-iћx.
Бұл өрнектерді біріктіре отырып, бір ғана тензорлық теңдеу түрінде былайша жазудың мүмкіндігі бар:
[ 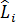 ,
, 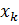 ]=iћ
]=iћ 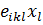 ,
,
Мұндағы 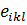 – Леви-Чивитаның антисимметриялы, үшінші рангілі бірлік псевдотензоры.
– Леви-Чивитаның антисимметриялы, үшінші рангілі бірлік псевдотензоры.
Осы теңдеуге ұқсас өрнектерді импульс пен бұрыштық момент операторларының коммутаторлары үшін де жазуға болады. Ол өрнек мынадай:
[ 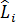 ,
, 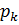 ]=iћ
]=iћ 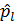 .
.
Ал бұрыштық момент проекцияларының операторлары өзара былай коммутацияланады:
[ 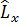 ,
, 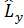 ]=iћ
]=iћ 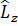 , [
, [ 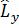 ,
, 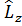 ]=iћ
]=iћ 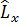 , [
, [ 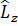 ,
, 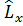 ]=iћ
]=iћ 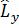
[ 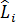 ,
, 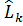 ]=iћ
]=iћ 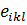 ,
, 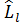 .
.
Бұрыштық момент квадратының операторын мына түрде
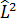 =
= 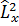 +
+ 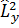 +
+ 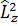 анықтайды.
анықтайды.
Ол бұрыштық момент проекцияларының операторларымен былайша коммутацияланады:
[ 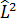 ,
, 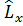 ]=0, [
]=0, [ 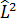 ,
, 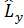 ]=0, [
]=0, [ 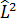 ,
, 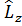 ]=0.
]=0.
Бұрыштық момент квадраты операторының меншікті мәндері мен меншікті функцияларын анықтайық. 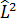 =-
=- 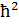 [
[ 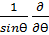 (sinӨ
(sinӨ 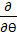 )+
)+ 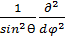 ] (1) өрнегіне сәйкес
] (1) өрнегіне сәйкес 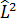 операторы радиалдық айнымалыға әсер етпейтін болғандықтан, қарастырып отырған теңдеудің шешімін мынадай Ψ(r,Ө,𝛗)=R(r)·Ψ(Ө,𝛗) бұрыштық айнымалылары ажыратылған функция түрінде іздестірудің мүмкіндігі бар. Онда меншікті мән мен меншікті функцияға арналған теңдеу жоғарыдағы (1) және
операторы радиалдық айнымалыға әсер етпейтін болғандықтан, қарастырып отырған теңдеудің шешімін мынадай Ψ(r,Ө,𝛗)=R(r)·Ψ(Ө,𝛗) бұрыштық айнымалылары ажыратылған функция түрінде іздестірудің мүмкіндігі бар. Онда меншікті мән мен меншікті функцияға арналған теңдеу жоғарыдағы (1) және 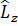 Ψ=
Ψ= 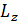 Ψ,
Ψ, 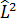 Ψ=
Ψ= 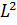 Ψ өрнектерінің негізінде мына түрде жазылады:
Ψ өрнектерінің негізінде мына түрде жазылады:
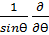 (sinӨ
(sinӨ 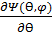 )+
)+ 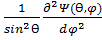 +
+ 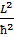 Ψ(Ө,𝛗)=0.
Ψ(Ө,𝛗)=0.
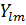 (Ө,𝛗)=
(Ө,𝛗)= 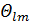 (Ө)·
(Ө)· 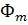 (𝛗),
(𝛗),
Мұндағы
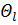 (Ө)=
(Ө)= 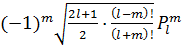 (cosӨ).
(cosӨ).
Ал Лежандрдың ассоцияцияланған полиномы
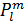 (x)=
(x)= 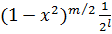 ·
· 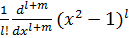 ,
,
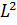 =
= 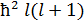
Бұрыштық момент квадраты операторының меншікті мәндері жоғарыдағы өрнекке сәцкес анықталып, меншікті функциялары сфералық функция болып табылады. Бұл сфералық функциялар өз кезегінде бұрыштық моменттің z өсіне проекция операторының 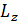 =mћ меншікті мәніне сәйкес келетін меншікті функциялары да болып табылады. Сонымен,
=mћ меншікті мәніне сәйкес келетін меншікті функциялары да болып табылады. Сонымен, 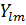 (Ө,𝛗) функциялары
(Ө,𝛗) функциялары 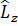 және
және 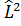 операторларының ортақ меншікті функциялары екен.
операторларының ортақ меншікті функциялары екен.
27.Орталық симметриялық өрістегі қозғалыс. Орталық симметриялық өрістегі қозғалыс интегралдары. Шредингердің радиал теңдеуі. Центрден тепкіш потенциал.
Орталық симметриялы өрістегі қозғалыс- кваттық механиканың маңызды есептерінің бірі. Осы есептер арқылы сутегі атомның теориясы, көп электронды атомдар мен молекудадардың күйлерін зерттейді.
Екі бөлшектің U(│r1-r2│) өзара әсерлесу энергиясын, массасы µ бөлшектің сыртқы ортылық симметриялық өрістергі пот енциалдық энергия қозғалысы деп аталады
Жалпы, орталық симметриялы өріс дегеніміз-кез келген нүктедегі потенциалдық энергиянын мәні оның ортасы деп нүктесінен ара қашықтығынан тәуелді өрісті айтамыз. Өріс орталық симметриялы болған соң осындай өрісті бөлшектің қозғалыс сфеpaлық кooрдинaт жүйесін қарастырады. Координат бас нүктесін өріс центрне орналастырады, полярлық өстін бағытын алады. Анықталған координат жүйесіндеегі өріс потенциалдық энергиясы V(r)=V(r) ºV(r). Кванттық есептерді осындай жүйеде қарастыру үшін декарттық айнымалылардың сфералық айнымалыларға яғни rº(x, y,z) ® (r,q,j) деп түрлендіреміз. Толқындық функция Y(r,t) = Y(x, y,z,t)® Y(r,q,j,t) деп түрленеді.
Кез-келген шаманың қоғалыс интегралын табу үшін, оның операторын гальтон операторымен коммутациялануы керек. Есептеулер арқылы H^,I^,L^²,L^ͥ операторың коммутацияландырайық. Осы жиындарға кіріп тұрған L^={L^x,L^y,L^z} oператоры прoeкциялары өзара коммутацияланбайтын соң осыған проекциялардың біреуін ғана кіргіземіз. Орталық симметриялы өрісте барлық бағыттары бірдей болғандықтан осылардың ішінен L- z осіне проекциясын алуға болады. Сонда коммутациялынған операторлардың жиыны осындай болады: H^,I^,L^²,L^z. Классикалық механикада импульс моменті проекцияларының орталық симметриялы өрісте сақталаталады. Осыны кванттық механикада да болатындығы осы жерде көрінеді.
Шредингердің радиал теңдеуі.Шредингер стационар теңдеуінен сфералық координат жүйесі осылаша жазылады
-ħ²/2µ[1/r²*∂/∂r(r²∂/∂r)-L^²/r²ħ²]ψ(r,θ,φ)=[E-V(r)]ψ(r,θ,φ)
Ocы теңдеуге ψ(r,θ,φ)=R(r)Y(θ,φ) функциясын қойсақ, одан әрі L^²Y(θ,φ)=ħ²l(l+1)Y(θ,φ) деп, белгісіз R(r) функциясынан мынандай тендеу аламыз
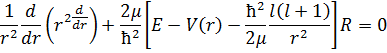
өріс үшін кванттық есептерді шешу Шредингердің радиалды тендеуін шешуге тура келеді . Бірақ кейбір жағдайда Шредингердің теңдеуін жеңілдету үшін R(r)=U(r)/r жаңа айналымға көшу қажет. Үсіндегі теңдеуден белгісіз U(r) функциясынан мынадай теңдеу аламыз
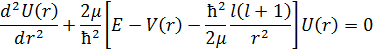
Бұл да Шредингердің радиалды теңдеуі. Осы өрнектен 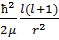 шамасын центрден тепкіш энергия деп атайды.
шамасын центрден тепкіш энергия деп атайды.
28.Шредингердің радиал теңдеуі үшін шекаралық шарт. Кванттық ротатор туралы есептің шешімі.
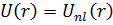 Осы формуладан Шредингердің радиалды теңдеуін аламыз
Осы формуладан Шредингердің радиалды теңдеуін аламыз
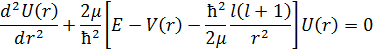
Мұндағы 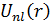 функциясының толқындық функ-ң радиал бөлігімен
функциясының толқындық функ-ң радиал бөлігімен 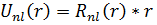 осылайша байланысқан
осылайша байланысқан
Радиалды айнымалы нөлден бастап шексіздікке дейін өзгереді. Осыған байланысты Шредингердің теңдеуінен координаттың бас нүктесіндегі потенциалдық энергиясы 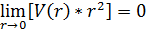 шарты орындалу тиіс. Бұл r→0 кезде, ׀V(r)׀ потенциалды 1/r² осымен салыстырғанда ол баяурақ өседі. Мұндай шартты тікбұрышты шұңқыр, гармониялық осциллятор, кулондық өріс тәрізді көптеген нақтылы әсерлесуді сипаттайтын потенциалдар қанағаттандырады. Бұл шарт орындалған жағдайда, r ® 0 кезде жоғарыдағы Шредингердің радиалды теңдеуіндегі
шарты орындалу тиіс. Бұл r→0 кезде, ׀V(r)׀ потенциалды 1/r² осымен салыстырғанда ол баяурақ өседі. Мұндай шартты тікбұрышты шұңқыр, гармониялық осциллятор, кулондық өріс тәрізді көптеген нақтылы әсерлесуді сипаттайтын потенциалдар қанағаттандырады. Бұл шарт орындалған жағдайда, r ® 0 кезде жоғарыдағы Шредингердің радиалды теңдеуіндегі 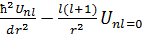 . Бұл теңдедің шешімі осындай түрде қарастырылады Unl→r²
. Бұл теңдедің шешімі осындай түрде қарастырылады Unl→r²
Сонымен бөлшектің энергиясы оң шама болған жағдайда Шредингердің радиалды теңдеуінен шекаралық шешімі 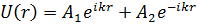 өрнегімен анықталады, осы өріс көзінен таралып жатқан немесе өріс көзінен жинақтадып жатқан сфералық толқындардың суперпозиция болады
өрнегімен анықталады, осы өріс көзінен таралып жатқан немесе өріс көзінен жинақтадып жатқан сфералық толқындардың суперпозиция болады
Толық энергия теріс болған кезде радиалды функция 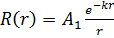 өрнегінен r→∞ бұл функ нөге ұмтылады. Яғни, бөлшек кенестігінің шектелген аймағынан финитті қозғалыс жасайды
өрнегінен r→∞ бұл функ нөге ұмтылады. Яғни, бөлшек кенестігінің шектелген аймағынан финитті қозғалыс жасайды
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|