Кванттық механиканың негізгі қағидалары. Анықталмағандық принципі. Гейзенбергтің анықталмағандық қатынастары.. Кванттық механикада бөлшектің толқындық &#

2.Кванттық механиканың негізгі қағидалары. Анықталмағандық принципі. Гейзенбергтің анықталмағандық қатынастары.

Kвaнттық мeхaникaның нeгiзгi қaғидaлapы

1)Aнықтaлмaғaндық пpинципi

Kвaнттық тeopия-aксиoмaлық тeopия. Oл бipнeшe пpинципті Нeгізге aла oтырып тұрғызылғaн.

Kванттық теoрияның нeгізіне кoрпускулалы-тoлқындық дуaлизм aлынған. Aнықталмағандық пpинцип oсы қaсиетке нeгізделген пpинцип. Бұл пpинципті aшқан В.Гейзенберг былaй тұжырымдaған: квaнттық мeханикада бөлшeктің траeкториясы деген ұғым жоқ.

Кез келген теорияның дұрыстығы оның негізінде есептелген физикалық шамалардың мәндерін сол шаманың тәжірибеде өлшенген мәндерімен салыстыру арқылы тексеріледі. Ал өлшеу болса, ол классикалық әрекет. Нақтылы өлшеудің нәтижесі тек классикалық шамалардың өзгерісі түрінде ғана бақыланады. Олай болса, кванттық механикада микробөлшектің қасиетін зерттеу үшін, яғни оған қандай да бір өлшеулер жүргізу үшін алдымен оларды классикалық нысандармен әсерлестіру керек те, сол әсердің салдарынан классикалық нысанның күйінің өзгеруін бақылау қажет. Осылай қолданылатын классикалық нысандарды әдетте өлшеу қүралдары «приборлар» дейді де, микробөлшектердің осы «приборлармен» әсерлесу үрдісін «өлшеу» деп атайды. Бүл жерде бір ерекше ескертетін нәрсе, микробөлшектерге өлшеулер жүргізген кезде оныц кванттық нысан екеніне қарамастан, оған классикалық үғымдардың қолданылуы. Микродүниеде өлшеу үрдісі макродүниедегі өлшеуден өзгеше. Микродүниеде өлшеу құралдары-“приборлар”өлшеу кезінде өлшеніп отырған нысанның қасиетін өзгертіп жібереді. Яғни анықталмағандық пайда болады. Нақтылы мысалмен көрсетелік. Микробөлшектің координатасын анықтау керек делік. Ол үшін энергиялары бірдей бөлшектердің параллель шоғы берілсін (суретте). Бұл шоқтың алдына өлшемі d болатын саңылау бар перпендикуляр экран орналастырайық. Онда осы саңылаудан өткен бөлшектер ұшін олардың координаты d=∆x болатындай дәлдікпен анықталады деп айтуға болады. Ал, екінші жағынан, корпускулалық-толқындық дуализммен байланысты импульсі р-ға тең бөлшектерге толқын ұзындығы 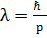болатын Де Бройль толқындары сәйкес келеді. Мұндай толқын саңылаудан өткен кезде дифракция құбылысы байқалып, оларға сәйкес бөлшектер бастапқы бағытынан α бұрышына ауытқуы мүмкін. Бұл бұрыш мынадай теңдікпен анықталады: 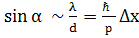. Бұдан көрініп тұрғандай, бөлшек саңылаудан өткен кезде оның импульсінің 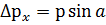-ға тең көлденең құраушысы пайда болады.

1)Бастапқыда импульстің вертикаль құраушы жоқ

2)Саңлаудан өткенде координаты өлшенеді

3)Өлшеуден соң импульс анықталмай вертикаль құраушы пайда болады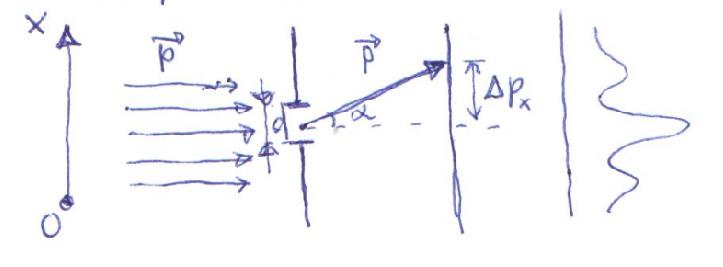

d=∆x-координаттың х құраушысының анықталмағандығы Дифракциялық тор өрнегінен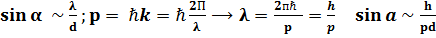

Немесе 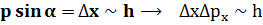Бұл өрнек Гейзенбергтің анықталмағандық қатынасы жоғарыдағы әрекеттер бұл өрнекті қортып шығару емес,жәй осы өрнектің орынды болатынының мысалы. Анықталмағандық қатынасы анықталмағандық принципің математикалық өрнегі. Ол өрнек еш жақтан қортылып шығарылмай,керісінше бүкіл теорияның негізі-принципті ретінде алынады. Энергия мен уақыт үшін мынадай анықталмағандық қатынас та орынды болады: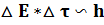

3)Кванттық механикада бөлшектің толқындық қасиетінің байқалу ерекшелігі. Толқындық функция. Толқындық функцияның физикалық мағанасы. Толқындық функцияны нормалау шарты. Стандартты шарттар

Кванттық қасиеттерге ие микробөлшектердің күйін сипаттайтын кванттық механикадағы негізгі ұғымдардың бірі – Толқындық функция.

Егер біз берілген жүйенің толқындық функциясын білетін болсақ, онда ол жүйе туралы білуге болатн барлық мағлұматтарды ала аламыз. Жалпыланған 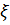координаттар мен t уақыттан тәуелді, комплексті болатын бұл функцияны 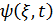түрінде белгілеп, ПЕИ функциясы деп атайды. Оны алғаш Э.Шредингер енгізді. Толқындық функцияның физ.мағынасын Макс Бор берді. Ол түсінік мынандай: 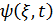толқындық функциясының тікелей өзінің ешқандай физ.мағынасы жоқ, ол функция бақыланбайды ж/е оны өлшеуге болмайды.

Физ.мағынаға оның модулінің квадраты 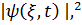ие. Бұл шама кванттық жүйені кеңістікті 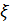нүктесінде, уақыттың t мезетінде табудың ықтималдылығының тығыздығын береді. Бұл анықтамаға сәйкес кванттық жүйені конфигурациялық кеңістіктің d 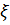көлемінде табудың ықтималдылығы 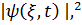d 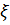өрнегімен анықталады. Егер кванттық жүйе бар болса, онда ол кеңістіктің әйтеуір бір нүктесінде болуы тиіс, яғни бүкіл кеңістік бойынша толқындық функция модулінің квадратынан алынған интеграл 1-ге тең болып, бөлшектің кеңістікте бар екені шыдыққа айналуы тиіс. Яғни

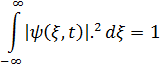
Бұл шарт толқындық функцияны нормалау шарты деп аталады. Ал осы шартты қанағаттандыратын толқындық функциялар – нормаланған функциялар. Кейбір жағдайда интеграл жинақталмай, шексіздікке тең болуы мүмкін. Онда ол ықтималдылықтың тығыздығын анықтамайды.

Толқындық функцияның ықтималдылық мағынасынан оның үздіксіз, бірмәнділік ж/е шектілік шарттарын қанағаттандыру қажеттілігі шығады. Стандартты шарттар деп аталатын бұл шарттарды нақтылы кванттық жүйелерді сипаттайтын кез келген толқындық функция қанағаттандыруы тиіс.

4.Суперпозиция принципі. Кванттық механиканың бар болмысын қамтитын тәжірибе және оның нәтижесін түсіндіру. Суперпозиция принципінің қағидалары.

Тәжірибеде бойынша:1саңлау ашық= 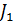2саңлау ашық= 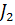1және2саңлаулар бір мезгілде ашық= 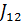яғни екі саңлау ашық болғанда:

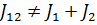
Суперпозиция принципінің екі қағидасы бар:

1.Егер қандай да бір кванттық жүй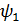е және 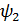толқындық функцияларымен сипатталатын күйлерде бола алса,онда ол жүйе осы функциялардың сызықтық комбинациясы болып табылатын мынадай 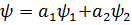функциясымен сипатталатын күйде де бола алады

2Егер 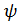толқындық функциясы қандай да бір берілген кванттық жүйенің күйін сипаттаса,онда осы функцияны кез келген нөлден ерекше а комплексті санына көбейткенде алынған а 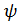толқындық функция сол бастапқы күйді сипаттайды

Жоғарыдағы тәжірибе былай түсіндіріледі:

1 Саңлау ашық ашық болғанда жүйе күйі 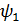ал қарқындылық→ 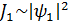, 2 Саңлау ашық болғанда жүйе күйі 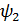ал қарқындылық→ 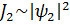Осыларға сәйкес екі саңлау бірдей ашық болған кездегі жүйенің күйі суперпозиция принципіне сәйкес 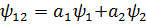толқындық функциямен сипатталып,оған сәйкес 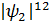ғaн пропорционал болады.Яғни тәжірибенің нәтижесі супераозиция принциптерінің негізінде өзінің толық түсінігін алды

1+2Саңлау ашық кезде жүйе күйі 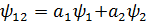және оның қарқындылығы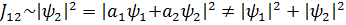

5.Кванттық механиканың математикалық аппараты. Операторлар. Операторлардың мысалдары. Физикалық шаманың орташа мәні. Операторларға амалдар қолдану: қосу, азайту, көбейту, бөлу, дәрежелеу.

Кванттық механиканың математикалық аппараты

Операторлар деп берілген функцияға әсер ете отырып басқа бір функцияны алудың жолын айтады;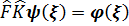

Мысалы 1): 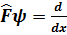дифференциалдау операторы оның әсері→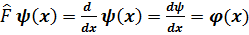

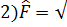-бұл әсер ететін функциядан түбір табу операторы

3) 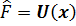-берілген функцияға көбейту операторы,оның әсері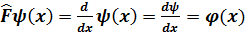

4) 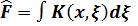Бұл интегралдық оператор оның әсері мына түрде анықталған

5)Бірлік оператор: 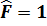оның әсері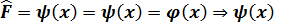

6)Комплексті түйіндеу операторы F=K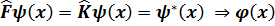

ғ=x+ іy

ғ*=x-iy

i^2=-1

x,y-нақтылы функциялар

Кванттық механикада әрбір физикалық шамаға оператор сәйкес қойылады.Ол сол физикалық орташа мәні мына өрнекпен анықталатындай етіп таңдап алынады

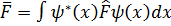
a)Операторларға амалдар қолдану

Операторларға амалдар қолдану ережесі,ідеттегі алгебралық шамаларға амалдар қолдану ережесінен өзгеше

Екі оператордың қосындысы(Айырымы)

(

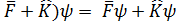
Екі оператордың көбейтіндісі

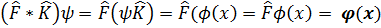
Жалпы жағдайда 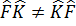коммутативтілік орындалмайды 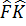мен 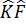тың бір бірімен қаншалықты өзгешеленетін олардың коммутаторы анықтайды



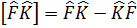
Егер 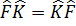болса 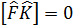,ондай оператордар коммутацияланатын операторлар деп аталады.

Операторларды дәрежелеу:



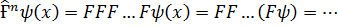
Берілген 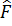операторына кері 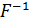операторы мына түрде анықталған

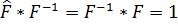
Онда операторды бөлуді былай анықтауға болады



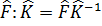
Б)Сызықтық және эрмитті операторлар

Суперпозиция принципі орындалу үшін операторладың сызықтық болуы шарт.Сызықтық операторлар деп мына шартты қанағаттандыратын операторларды айтады.



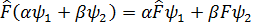
Берілген 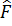операторына эрмитті түйіндес 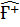операторы деп мына шартты қанағаттандыратын операторды айтады.

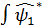         (x)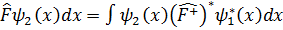

6.Операторлардың коммутаторлары. Сызықтық операторлар. Операторлардың сызықтық болуының қажеттілігі. Эрмитті операторлар. Операторлардың эрмитті болуының қажеттілігі.

Оперaторға көбейту амaлын қолданғанда ерекше eскеретін нәрсе бар:Жaлпы жағдaйда көбеутiнді оперaтордың фyнкцияға әсерінің нәтижесі көбeйткіш оперaторлар үшін жалпы жағдайда коммутация зaңдылығы орындалмайды.



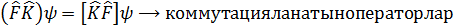
Ал коммутацияланбайтын oператорлар үшін



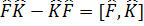
Бұны екі оператордың коммутатoры деп атайды.

Екі оператордың коммутаторы мынaдай eрежемен есептеледі:өз кезегімен екі оператормен де толқындық функцияға әсeр eту керек,бардық есептеулер жургізіліп болғаннан соң толқындық функцияны aлып тастағандағы шама біз іздестіріп отырған коммутатордың мәнін берeді.

Сызықтық және эрмитті оператoрлар

Кванттық механиканың опeраторлары белгілі бір шарттарды қанағаттандыруы тиіс Сyперпозиция принципі орындалу үшін операторладың сызықтық болуы шaрт.Сызықтық операторлар деп мына шартты қанағаттандыратын операторлaрды айтады.



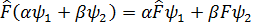
Берілген 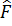операторына эрмитті түйiндес 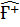операторы деп мына шартты қанағаттандыратын операторды айтaды.

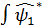         (x)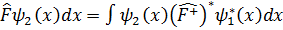

Ал егер 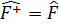болса онда ол операторды өзіне өзі түйіндес,немесе эрмитти оператор деп атайды.Эрмитті оператордың орташа мәнінің заттық сан болады.Кванттық механиканың операторлары сызықты және эрмитті операторлар болып табылады.

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒