Задача 3.11.. Задача 4.12.

⇐ ПредыдущаяСтр 4 из 7Следующая ⇒

Задача 3.11.

Найти решения уравнения, удовлетворяющие заданным условиям:

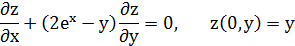
Решение.

Это уравнение – линейное однородное. Составим систему характеристик.

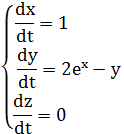
Из третьего уравнения: z=C₁ – один первый интеграл.

Для нахождения еще одного первого интеграла исключим из системы dt и приведем к соотношению:

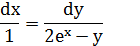
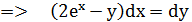
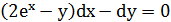
Получили уравнение, приводящееся к уравнению в полных дифференциалах.

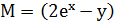
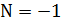
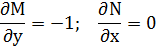
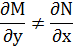
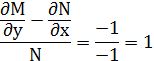
=> Существует интегрирующий множитель вида μ=μ(x)

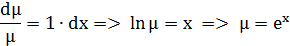
Домножим уравнение на .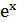

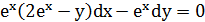
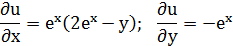
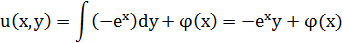
Подберем 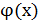так, чтобы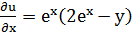

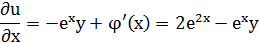
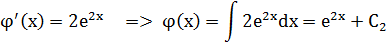
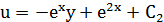
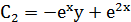- еще один первый интеграл системы

Общее решение имеет вид:

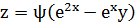, где 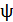– произвольная дифференцируемая функция

Используя начальное условие, запишем систему:

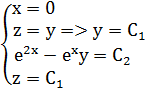
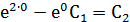
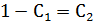
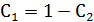
Общее решение в явном виде имеет вид:

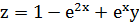
Задача 4.12.

Исследовать устойчивость нулевого решения, построив функцию Ляпунова и применив теоремы Ляпунова или Четаева.

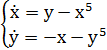
Решение.

Построим функцию Ляпунова. Будем искать её в виде: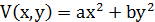

Тогда производная этой функции в силу системы:

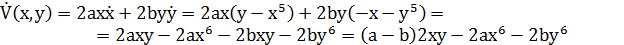
Пусть b=a, b>0, a>0:

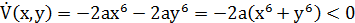
Возьмём a=b=1:

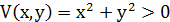
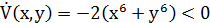– отрицательно определена

Теорема Ляпунова об асимптотической устойчивости: пусть в некоторой окрестности U положения равновесия x=a системы существует непрерывно дифференцируемая положительно определенная функция V(x) такая, что ее производная 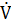в силу этой системы отрицательно определена в окрестности U точки x=a. Тогда положение равновесия асимптотически устойчиво по Ляпунову.

Согласно этой теореме нулевое решение исходной системы асимптотически устойчиво по Ляпунову.

Проверим устойчивость с помощью математического пакета Maple17. Для этого построим фазовый портрет системы в окрестности точки (0,0) (текст программы приведен в приложении).

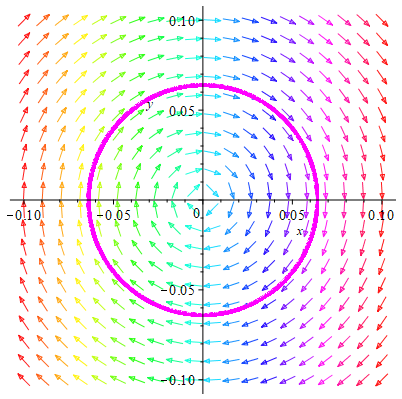
рис.4.1

⇐ Предыдущая 1 2 345 6 7 Следующая ⇒