ВАРИАНТЫ ЗАДАНИЙ.. Задача 1.7.

ВАРИАНТЫ ЗАДАНИЙ.

Задача 1.7. Найти особые точки следующих систем. Определить их тип. Построить схематически фазовый портрет в окрестности каждой особой точки.

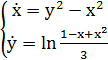
Задача 2.13. Найдя первый интеграл, изобразить фазовый портрет уравнения на плоскости .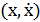

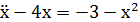
Задача 3.11. Найти решения уравнения, удовлетворяющие заданным условиям:

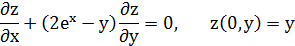
Задача 4.12. Исследовать устойчивость нулевого решения, построив функцию Ляпунова и применив теоремы Ляпунова или Четаева.

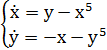
Задача 5.16. С помощью теоремы об устойчивости по первому приближению исследовать на устойчивость все состояния равновесия системы

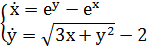
Задача 6.7. Используя теорему Пуанкаре-Бендиксона, доказать существование цикла у уравнения или системы

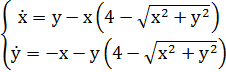
Задача 7.30. Методом Пуанкаре найти приближенно периодическое решение данного уравнения.

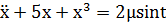
Задача 1.7.

Найти особые точки следующих систем. Определить их тип. Построить схематически фазовый портрет в окрестности каждой особой точки.

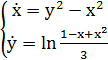
Решение.

Для нахождения особых точек решим систему уравнений: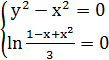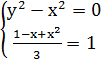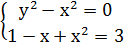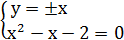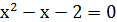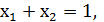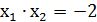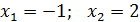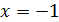

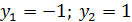
При :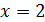

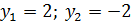
Итак, особыми точками будут: M₁(-1;-1), M₂(-1;1), M₃(2;2), M₄(2;-2)

Найдем матрицу Якоби системы:

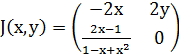
Для точки M₁(-1;-1) имеем

Для точки M₂(-1;1) имеем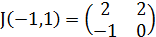

Для точки M₃(2;2) имеем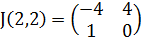

Для точки M₄(2;-2) имеем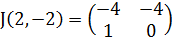

1. Рассмотрим точку M₁(-1;-1).

Найдём собственные значения для матрицы

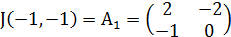
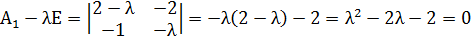
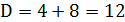
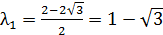
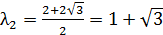
Так как собственные значения матрицы – вещественные числа разных знаков, то точка покоя M₁(-1;-1) является точкой типа «седло». Для построения фазового портрета в окрестности M₁(-1;-1), найдем собственные векторы, соответствующие найденным собственным значениям:

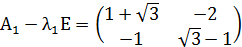
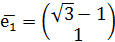
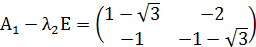
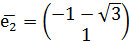
Согласно теореме, определяющей поведение траекторий нелинейной системы вблизи особой точки типа «седло», существуют ровно две траектории u₁ и u₂, которые при t→+∞ асимптотически приближаются к точке покоя. Эти две траектории вместе с точкой покоя образуют гладкую кривую, касающуюся в особой точке прямой, проведённой на плоскости в направлении собственного вектора 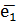, соответствующего собственному значению λ₁. Существуют ровно две траектории v₁ и v₂, которые при t→-∞ асимптотически приближаются к точке покоя. Эти траектории вместе с точкой покоя образуют гладкую кривую, касающуюся в особой точке прямой, проведённой на плоскости в направлении собственного вектора 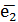, соответствующего собственному значению λ₂. Поведение фазовых траекторий в окрестности точки M₁ показано на рисунке 1.1, построенном с помощью программы Maple17 (текст программы приведён в приложении), и на рисунке 1.2, построенном вручную:

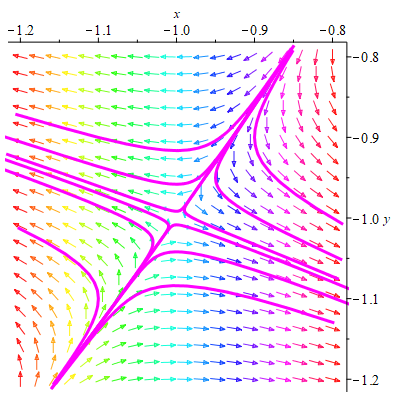
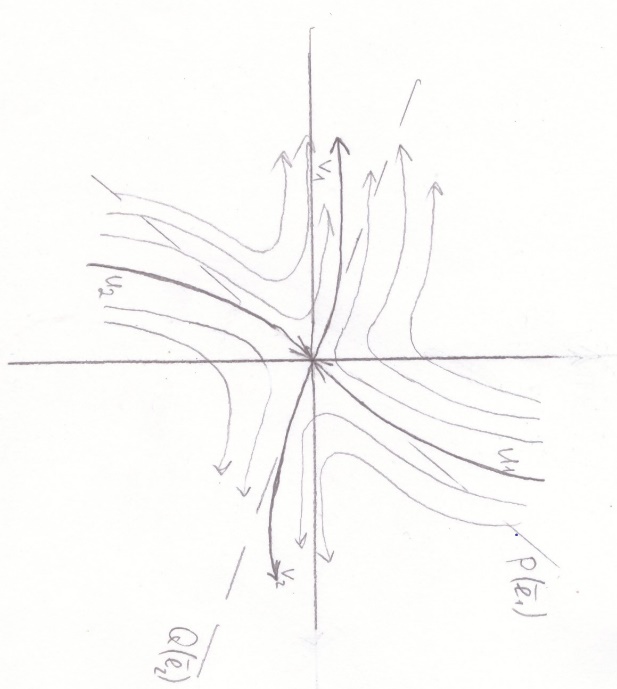
рис.1.1 рис.1.2

2. Рассмотрим точку M₂(-1;1).

Найдём собственные значения для матрицы

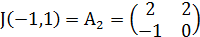
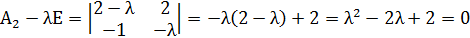
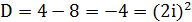
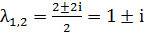
Так как собственные значения матрицы – комплексно сопряженные числа и α>0, то точка покоя M₂(-1;1) является точкой типа «неустойчивый фокус».

Для выяснения направления раскручивания спирали выберем точку, близкую к точке M₂. Возьмем точку с координатами (-1;0,998). Подставим координаты этой точки в правые части исходной системы:

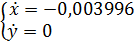
Выпускаем из выбранной точки вектор 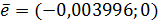. Спираль раскручивается против часовой стрелки.

Поведение фазовых траекторий в окрестности точки M₂ показано на рисунке 1.3, построенном с помощью программы Maple17 (текст программы приведен в приложении), и на рисунке 1.4, построенном вручную:

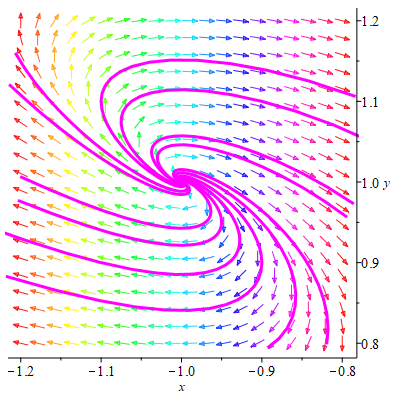
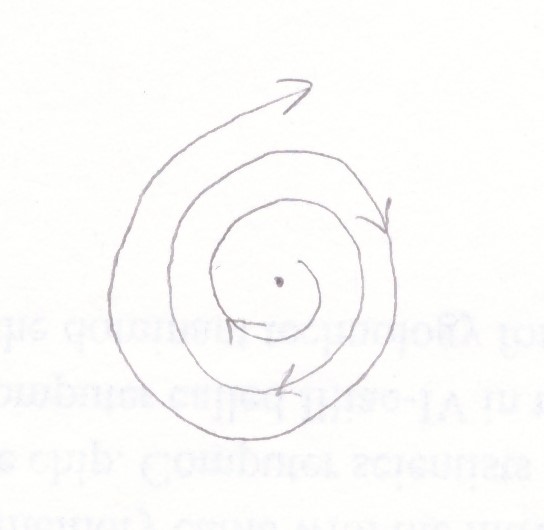
рис.1.3 рис.1.4

3. Рассмотрим точку M₃(2;2).

Найдём собственные значения для матрицы

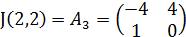
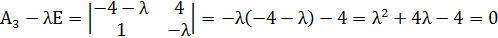
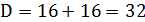
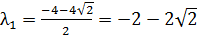
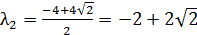
Так как собственные значения матрицы – вещественные числа разных знаков, то точка покоя M₃(2;2) является точкой типа «седло». Для построения фазового портрета в окрестности M₃(2;2), найдем собственные векторы, соответствующие найденным собственным значениям:

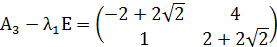
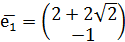
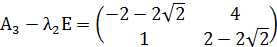
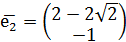
Согласно теореме, определяющей поведение траекторий нелинейной системы вблизи особой точки типа «седло», существуют ровно две траектории u₁ и u₂, которые при t→+∞ асимптотически приближаются к точке покоя. Эти две траектории вместе с точкой покоя образуют гладкую кривую, касающуюся в особой точке прямой, проведённой на плоскости в направлении собственного вектора 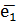, соответствующего собственному значению λ₁. Существуют ровно две траектории v₁ и v₂, которые при t→-∞ асимптотически приближаются к точке покоя. Эти траектории вместе с точкой покоя образуют гладкую кривую, касающуюся в особой точке прямой, проведённой на плоскости в направлении собственного вектора 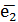, соответствующего собственному значению λ₂. Поведение фазовых траекторий в окрестности точки M₃ показано на рисунке 1.5, построенном с помощью программы Maple17 (текст программы приведен в приложении), и на рисунке 1.6, построенном вручную:

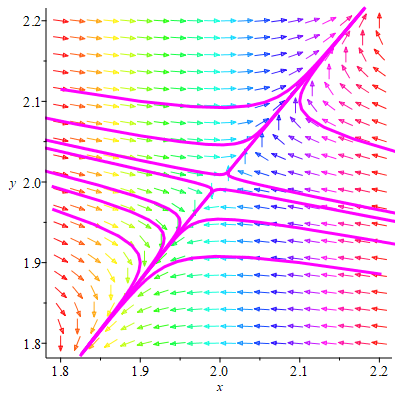
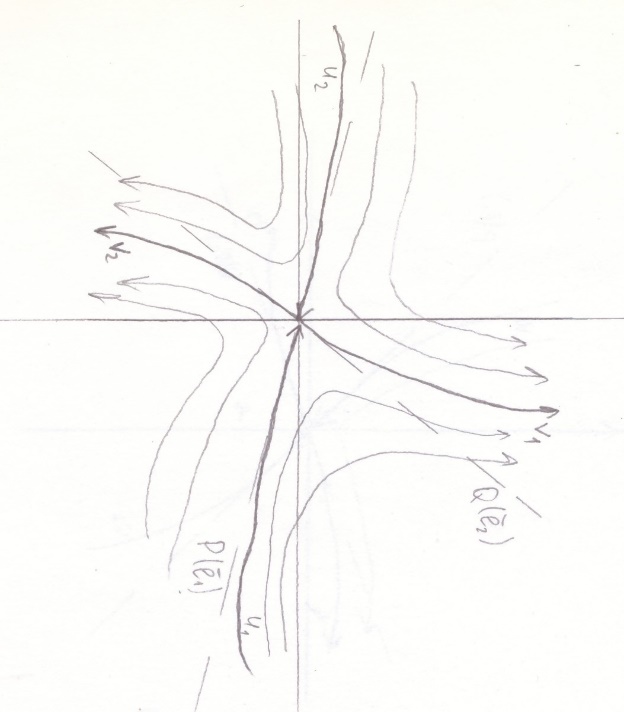
рис.1.5 рис.1.6

4. Рассмотрим точку M₄(2;-2).

Найдём собственные значения для матрицы

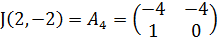
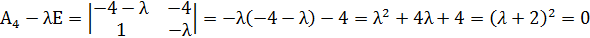
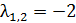
Так как собственные значения матрицы – кратные числа, следовательно нельзя сделать вывод о типе особой точки.

На рисунке 1.7 изображен фазовый портрет системы, построенный с помощью математического пакета Maple17 (текст программы приведен в приложении).

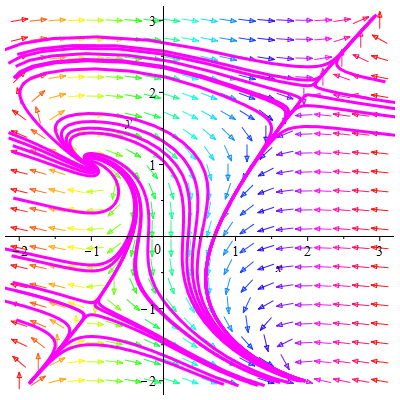
рис.1.7

⇐ Предыдущая 123 4 5 6 7 Следующая ⇒