Контакты

Случайная статья

Задача 2.13.

⇐ ПредыдущаяСтр 3 из 7Следующая ⇒

Задача 2.13.

Найдя первый интеграл, изобразить фазовый портрет уравнения на плоскости .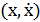

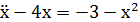
Решение.

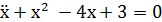
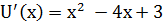
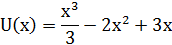
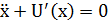
Домножим полученное уравнение на :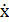

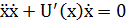
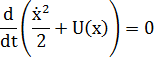
Можем переписать в виде:

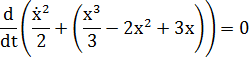
Первый интеграл уравнения имеет вид: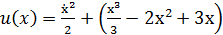

Построим фазовый портрет уравнения на плоскости 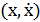, 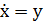. Тогда уравнение 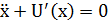будет эквивалентно системе:

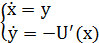
Найдем точки покоя полученной системы:

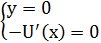
Очевидно, что точками покоя на плоскости 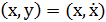будут точки вида 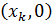, в которых .

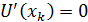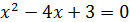
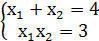
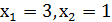
Производная функции положительна на промежутках 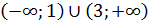и функция возрастает на этих промежутках, и производная отрицательна на промежутке 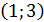, соответственно функция убывает на этом промежутке.

Таким образом,

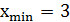– точка минимума функции

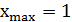– точка максимума функции

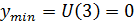
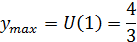
Построим схематически график функции U(x) и на его основе построим фазовый портрет уравнения (рис.2.1).

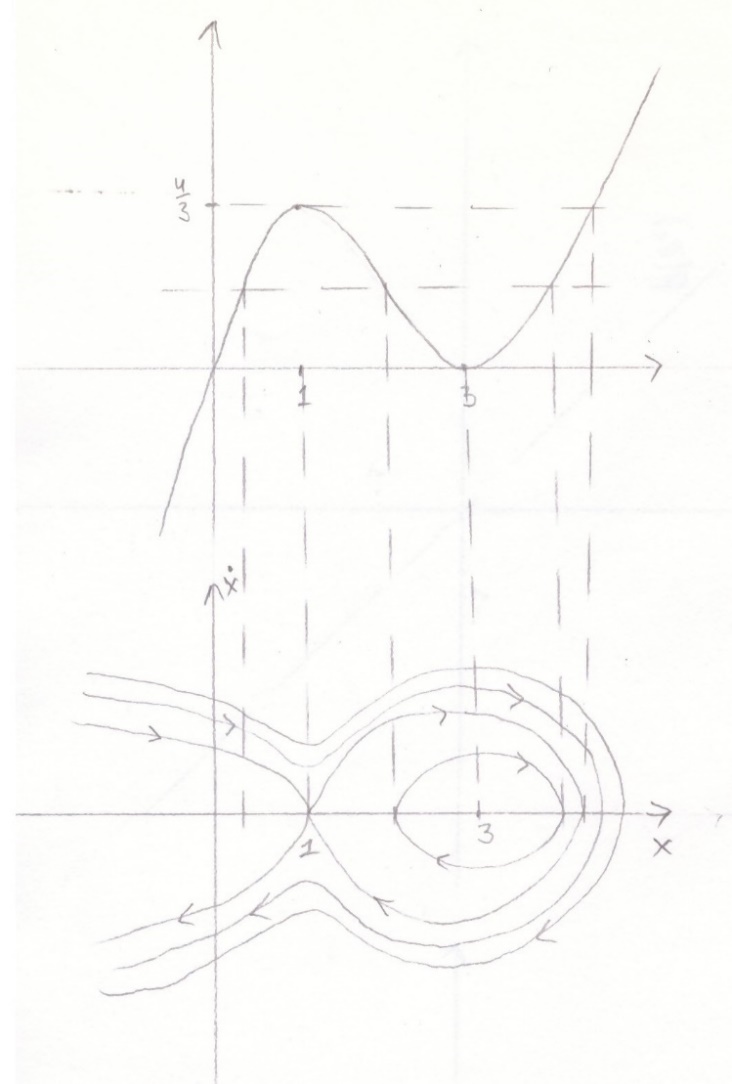
рис.2.1

Проверим данные построения с помощью математического пакета Maple17 (текст программы приведен в приложении).

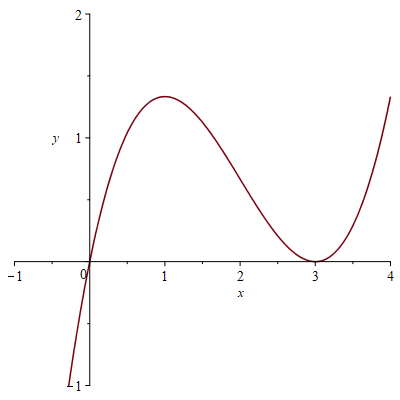
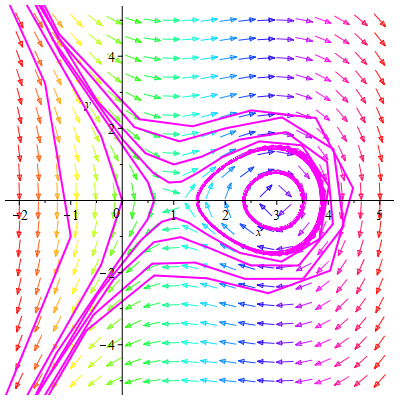
рис.2.2 рис.2.3

Проверим движение в окрестности центра на синхронность. Для этого в разных значениях Е рассчитаем значение

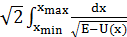
E=0,1

x_min=2,66445

x_max=3,30145

T=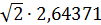

E=0,2

x_min=2,5112

x_max=3,41892

T=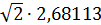

E=0,3

x_min=2,38581

x_max=3,50661

T=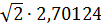

Построим график зависимости E(T) с помощью математического пакета Maple17 (текст программы приведен в приложении):

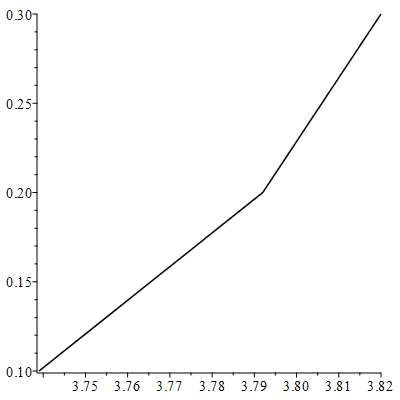
рис.2.4

Так как E(T)≠const, значит движение не изохронное.

⇐ Предыдущая 1 234 5 6 7 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.