Соотношения упругости

5.4. Соотношения упругости

В двух предыдущих главах рассматривались закономерности напряженного и деформированного состояний, отражающих две стороны одного и того же явления. Результаты механических испытаний материалов составляют основу физических уравнений, устанавливающих связь между напряжениями и деформациями.

Напряжения в упругом теле образуют физическое силовое поле, которое можно охарактеризовать некоторой потенциальной функцией (потенциалом), позволяющей выразить компоненты напряжения в виде производных. Опыты показали, что для создания напряженного состояния необходимо затратить энергию, которая переходит во внутреннюю механическую энергию. Ее накопление связывают с работой внутренних сил.

На бесконечно малом этапе деформирования с приращениями
деформаций dε_х,…,dγ_zx работу внутренних сил можно вычислить как произве-

дение постоянной силы на путь с точностью до бесконечно малых второго порядка. Выделим из тела бесконечно малый параллелепипед с ребрами dx, dy, dz. Бесконечно малым площадкам можно приписывать постоянные напряжения и перемещения.

Работа внутренних продольных сил, которым соответствуют напряжения σ_x (рис. 5.6, а или рис. 5.6, б), вычисляется как произведение силы σ_хdydz на перемещение dε_xdx т.е. σ_хdε_xdxdydz. Аналогично вычисляется работа двух других продольных сил: σ_ydε_ydxdydz, σ_zdε_zdxdydz .

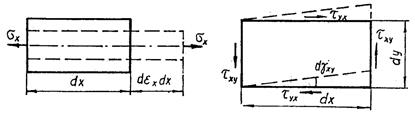
Работа внутренних сдвигающих сил, которым соответствуют напряжения τ_ху (рис. 5.7,а или 5.7,б), вычисляется как произведение силы τ_хуdydz на перемеще-ния dγ_xydx, т.е. τ_хуdγ_xydxdydz. Аналогично вычисляется работа двух других сдвигающих сил: τ_yzdγ_yzdxdydz, τ_zxdγ_zxdxdydz.

Элементарная удельная работа внутренних сил dũ (работа на бесконечно малом этапе деформирования, приходящаяся на единицу объема) есть сумма полученных величин работ, разделенная на объем бесконечно малого параллелепипеда dxdydz:

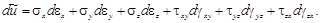
а а

б б

Рис. 5.6 Рис. 5.7

В упругом теле удельная работа внутренних сил не зависит от пути дости-жения того или иного деформированного состояния, а является функцией лишь окончательных значений деформации:

ũ=ũ(ε_x,ε_y,ε_z,γ_xy,γ_yz,γ_zx).

Приращение этой функции с точностью до бесконечно малых второго порядка можно заменить ее полным дифференциалом:

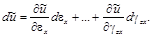
Сравнивая два выражения для dũ и учитывая независимость приращений деформаций, получаем соотношения:

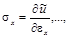
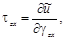
которые позволяют считать ũ потенциалом. Эти соотношения называются формулами Грина (по имени английского ученого, впервые их получившего). Они применимы как для линейно-, так и для нелинейно-упругого тела при малых деформациях.

Предполагалось, что в недеформированном состоянии напряжения равны нулю. После снятия нагрузки тело приходит в свое естественное недеформированное состояние и, следовательно, восстанавливает свою первоначальную форму. Происходит это за счет накопленной данным материалом потенциальной энергии деформации, численно равной работе внутренних сил.

Вследствие этого удельная потенциальная энергия деформации ū также должна рассматриваться как упругий потенциал поля напряжений. Следовательно,

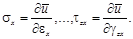
Потенциал линейной теории деформирования представляется многочленом второй степени. Потенциал поля напряжений, представленный многочленом третьей степени по инвариантам тензора дефор-маций, соответствует квадратичной форме физичес-кого закона, т.е. физической нелинейности низшего порядка.

Введем в рассмотрение удельную дополнительную энергию (энергию напряжений), элементарная вели-чина которой

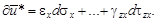
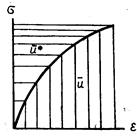
В геометрическом смысле энергия 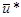является

Рис. 5.8 дополнением энергии 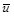, поскольку вместе они составляют прямоугольник, изображенный на рис. 5.8. При линейном физическом законе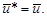

Приращение этой функции можно заменить ее полным дифференциалом:

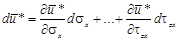Соотношения

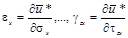
называются формулами Кастильяно.

⇐ Предыдущая 14 15 16 17 181920 21 22 23 Следующая ⇒