Дифференциальные уравнения равновесия для внутренних усилий в поперечных сечениях стержней

2.3. Дифференциальные уравнения равновесия для внутренних усилий в поперечных сечениях стержней

В общем случае нагрузка на стержень может быть задана интенсивностью сил с составляющими 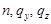, и интенсивностью моментов с составляющими 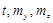. Возможна также нагрузка, сосредоточенная в отдельных точках. Для бесконечно малой части стержня (рис.2.3) составим дифференциальные уравнения равновесия.

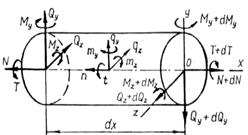
Рис. 2.3

Из условий 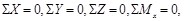следуют уравнения:

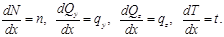
Из условий 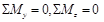получаем:

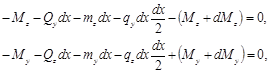
откуда, пренебрегая бесконечно малыми второго порядка, находим

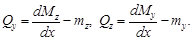
Подставляя выражения 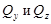в соответствующие дифференциальные уравнения, получаем

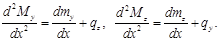
Интегрируя полученные шесть уравнений, находим выражения для внутренних усилий:

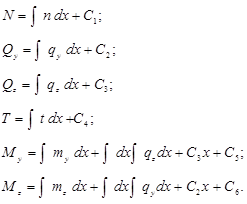
Постоянные интегрирования С_i (i=1,2,...,6) определяются из граничных условий для рассматриваемых внутренних усилий.

Поскольку дифференциальные уравнения выражают равновесие любого бесконечно малого элемента стержня, то удовлетворение им означает выполнение условий равновесия стержня в целом.

Дифференциальные зависимости используются для проверки результатов, полученных с помощью алгебраических уравнений равновесия. Они позволяют, например, по эпюре 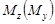определить характер эпюры 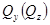. В частности, на участках, где 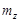=0 ( 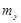=0), т.е. при соблюдении зависимостей

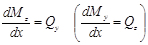
можно установить, что при М_z = const имеем Q_y = 0(при М_y =const имеем Q_z = 0). Переменная величина 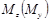достигает экстремальных значений в точках, где Q_y = 0(Q_z = 0).

При определении внутренних усилий из уравнений равновесия целесообразно нагрузку на поверхности переносить в соответствующие точки на оси стержня с соблюдением условий статической эквивалентности. Полученная таким образом силовая схема является составной частью так называемой расчетной схемы (системы), когда брус представляется его осью.

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒