
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Конус второго порядка
Конус второго порядка
Исследуем уравнение поверхности
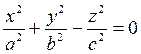 (12.35)
(12.35)
Пересечем поверхность (12.35) плоскостями z = h. Линия пересечения 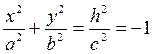 , z = h. При h = 0 она вырождается в точку (0;0;0). При h ≠ 0 в сечении будем получать эллипсы
, z = h. При h = 0 она вырождается в точку (0;0;0). При h ≠ 0 в сечении будем получать эллипсы
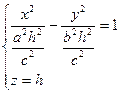
Полуоси этих эллипсов будут возрастать при возрастании |h|.
Рассечем поверхность (12.35) плоскостью Oyz (х = 0). Получится линия
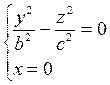
распадающаяся на две пересекающиеся прямые
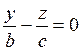 и
и 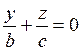
При пересечении поверхности (12.35) плоскостью у = 0 получим линию
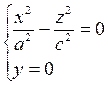
также распадающуюся на две пересекающиеся прямые
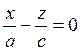 и
и 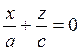
Поверхность, определяемая уравнением (12.35), называется конусом второго порядка, имеет вид, изображенный на рисунке 96.
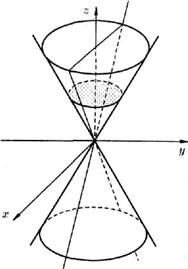
Рис. 96.
Поверхности, составленные из прямых линий, называются линейчатыми. Такими поверхностями являются цилиндрические, конические поверхности, а также однополостный гиперболоид и гиперболический параболоид.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|