Эллиптический параболоид. Гиперболический параболоид

Эллиптический параболоид

Исследуем поверхность, заданную уравнением

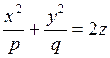(12.33)

где р > 0, q > 0. Рассечем поверхность (12.33)плоскостями z = h. В сечении получим линию, уравнения которой есть

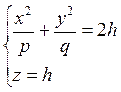
Если h < 0, то плоскости z = h поверхности не пересекают; если h = 0, то плоскость z = 0 касается поверхности в точке (0;0;0); если h > 0, то в сечении имеем эллипс, уравнение которого имеет вид,

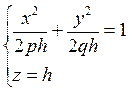
Его полуоси возрастают с ростом h. При пересечении поверхности (12.33) координатными плоскостями Oxz и Oyz получатся соответственно параболы 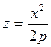и 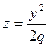. Таким образом, поверхность, определяемая уравнением (12.33), имеет вид выпуклой, бесконечно расширяющейся чаши (см. рис. 94). Поверхность (12.33) называется эллиптическим параболоидом.

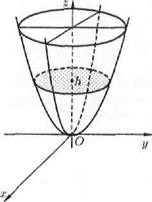
Рис. 94.

Гиперболический параболоид

Исследуем поверхность, определяемую уравнением

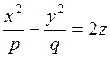(12.34)

где р > 0, q > 0. Рассечем поверхность (12.34) плоскостями z = h. Получим кривую

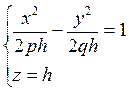
которая при всех значениях h ≠ 0 является гиперболой. При h > 0 ее действительные оси параллельны оси Ох; при h < 0 параллельны оси Оу; при h = 0 линия пересечения 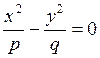распадается на пару пересекающихся прямых 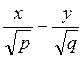и 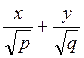. При пересечении поверхности плоскостями, параллельными плоскости Oxz (у = h), будут получаться параболы

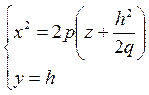
ветви которых направлены вверх. При у=0 в сечении получается парабола

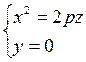
вершиной к начале координат и осью симметрии Oz.

Пересекая поверхность (12.34) плоскостями х =h, получим параболы у² = 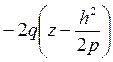ветви которых направлены вниз.

Анализ линии пересечения позволяет определить вил поверхности: она имеет вид седла (см. рис. 95). Поверхность (12.34) намывается гиперболическим параболоидом.

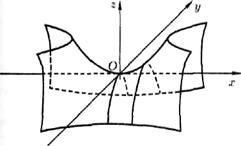
Рис. 95.

⇐ Предыдущая 1 2 3 456 Следующая ⇒