Эллипсоид

Эллипсоид

Исследуем поверхность, заданную уравнением

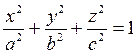(12.28)

Рассмотрим сечения поверхности (12.28) с плоскостями, параллельными плоскости хОу. Уравнения таких плоскостей: z = h, где h — любое число.

Линия, получаемая в сечении, определяется двумя уравнениями

(12.29)

Исследуем уравнения (12.29):

а) Если |h| > с, с > 0, то 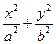< 0. Точек пересечения поверхности (12.28) с плоскостями z = h не существует.

б) Если |h| = с, т. е. h = ±с, то 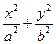= 0. Линия пересечения (12.29) вырождается в две точки (0;0;с) и (0;0;— с). Плоскости z = с и z =- с касаются данной поверхности.

в) Если |h| < с, то уравнения (12.29) можно переписать в виде:

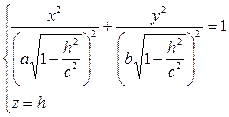
Как видно, линия пересечения есть эллипс с полуосями (см. рис. 91)

При этом чем меньше |h|, тем больше полуоси а₁ и b₁. При h = 0 они достигают своих наибольших значений: а₁ = а, b₁ = b. Уравнения (12.29) примут вид

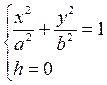
Аналогичные результаты получим, если рассмотрим сечения поверхности (12.28) плоскостями х = h и у = h.

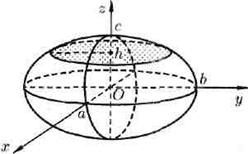
Рис. 91.

Таким образом, рассмотренные сечения позволяют изобразить поверхность (12.28) как замкнутую овальную поверхность. Поверхность (12.28) называется эллипсоидом. Величины a, b и с называются полуосямиэллипсоида. Если все они различны, то эллипсоид называется трехосным; если какие-либо две полуоси равны, трехосный эллипсоид превращается в эллипсоид вращения; если а = b = с, то — в сферу х² + у² + z² = a².

⇐ Предыдущая 1 234 5 6 Следующая ⇒