
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Однополостный гиперболоид. Двухполостный гиперболоид
Однополостный гиперболоид
Исследуем поверхность, заданную уравнением
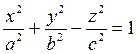 (12.30)
(12.30)
Пересекая поверхность (12.30) плоскостью z = h, получим линию пересечения, уравнения которой имеют вид
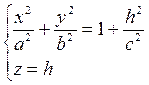 или
или 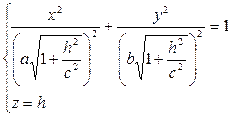
Как видно, этой линией является эллипс с полуосями
a1 = 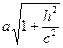 и b1 =
и b1 = 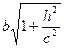
Полуоси а1 и b1 достигают своего наименьшего значения при h = 0: а1 = a, b1 = b. При возрастании |h| полуоси эллипса будут увеличиваться.
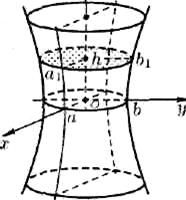
Рис. 92.
Если пересекать поверхность (12.30) плоскостями х = h или у = h, то в сечении получим гиперболы. Найдем, например, линию пересечения поверхности (12.30) с плоскостью Oyz, уравнение которой х = 0. Эта линия пересечения описывается уравнениями
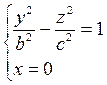
Как видно, эта линия есть гипербола (см. рис. 92).
Анализ этих сечений показывает, что поверхность, определяемая уравнением (12.30), имеет форму бесконечной расширяющейся трубки. Поверхность (12.30) называется однополостным гиперболоидом.
Замечание: можно доказать, что через любую точку гиперболоида (12.30) проходят две прямые, лежащие на нем.
Двухполостный гиперболоид
Пусть поверхность задана уравнением
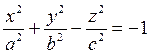 (12.31)
(12.31)
Если поверхность (12.31) пересечь плоскостями z = h, то линия пересечения определяется уравнениями
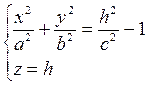 (12.32)
(12.32)
Отсюда следует, что:
а) если |h| < с, то плоскости z = h не пересекают поверхности;
б) если |h| = с, то плоскости z = ±с касаются данной поверхности соответственно в точках (0; 0; с) и (0; 0; -с).
в) если |h| > с, то уравнения (12.32) могут быть переписаны так
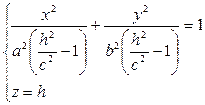
Эти уравнения определяют эллипс, полуоси которого возрастают с ростом |h|.
Пересекая поверхность (12.31) координатными плоскостями Oyz (х = 0) и Oxz (у = 0), получим в сечении гиперболы, уравнения которых соответственно имеют вид
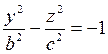 и
и 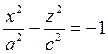
У обеих гипербол действительной «осью является ось Oz. Метод сечения позволяет изобразить поверхность (см. рис. 93), определяемую уравнением (12.31). как поверхность, состоящую из двух полостей, имеющих форму выпуклых неограниченных чаш. Поверхность (12.31)называется двухполостным гиперболоидом.
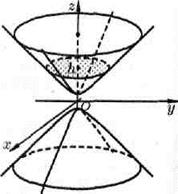
Рис. 93.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|