«При делении остаток всегда меньше делителя».

Определение: Разделить с остатком число а на число b – это значит найти такие q и r, что а=bq+r, где  b> r> 0.

На первом уроке М3М, ч. 2, стр. 26 рассматривают конкретный смысл деления с остатком.

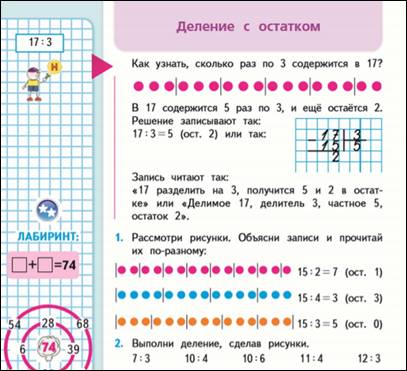
Для этого берут задания на деление по содержанию и разбирают его, составляя графическую модель и запись.

17: 3

Надо узнать, сколько раз по 3содоржится в 17?

В 17 содержится 5 раз по 3 и еще остается 2. Решение записываем так:

17: 3=5 (ост. 2) или так _17 3.

                                       15 5

                                         2

Таким образом, в результате получили 2 числа – частное и остаток.

После объяснения предлагают упражнения на закрепление, в которых, чтобы найти результат деления с остатком, надо выполнить модель.

Это такие задания:

1. По рисунку составь запись.

                                                                            ( 9: 2=4 (ост. 1))

2. По записи составь рисунок.

9: 2=4 (ост. 1)

3. Установите соответствие между несколькими записями и несколькими рисунками.        

 (рисунки и записи к упражнениям с 3 по 7 составьте самостоятельно)

4. Исправь ошибку в записи, чтобы она соответствовала рисунку.

5. Исправь ошибку в рисунке, чтобы он соответствовал записи.

6. Закончи рисунок по этой записи.

7. Закончи запись по этому рисунку.

и т. д.

Найдите такие задания в учебниках.

На следующем уроке М3М, ч. 2, стр. 27 выводят правило:

«При делении остаток всегда меньше делителя».

Для доказательства этого правила предлагаем детям выполнить задания:

а) Найди остатки при делении на 2. Сделай рисунки и закончи каждую запись.

7: 2                       

9: 2

13: 2                       

Дети по рисунку заканчивают записи, затем сравнивают получившиеся остатки с делителем 2. Это 0 и 1, они < 2, следовательно, остаток меньше делителя.

б) Аналогично делим на 3 и для этого строим модели в тетради или на парте.

6: 3    

13: 3   

17: 3

Сравниваем остатки с делителем (получаем 0, 1, 2 < 3), следовательно, получаем такой же вывод: остаток меньше делителя.                                          

в) Аналогично делим на 4 и для этого строим модели.

8: 4              

9: 4

10: 4

11: 4

Сравниваем остатки с делителем (0, 1, 2, 3< 4), следовательно, получаем такой же вывод.

г) Делаем общий вывод: остаток всегда меньше делителя.

Затем предлагаем задания на закрепление этого вывода:

- Может ли при делении на 6 получиться остаток 7? (нет, так как остаток всегда меньше делителя).

- Какие остатки могут получиться при делении на 8?

и т. д.

На страницах М3М, ч. 2, стр. 28 - 29 детей знакомят с алгоритмами деления с остатком.