
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
СВОД ПРАВИЛ 12 страница
8. 2. Расчет элементов железобетонных конструкций
по предельным состояниям второй группы
Общие положения
8. 2. 1. Расчеты по предельным состояниям второй группы включают:
расчет по образованию трещин;
расчет по раскрытию трещин;
расчет по деформациям.
8. 2. 2. Расчет по образованию трещин производят, когда необходимо обеспечить отсутствие трещин (см. 4. 3), а также как вспомогательный при расчете по раскрытию трещин и по деформациям.
8. 2. 3. При расчете по образованию трещин в целях их недопущения коэффициент надежности по нагрузке принимают 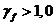 (как при расчете по прочности). При расчете по раскрытию трещин и по деформациям (включая вспомогательный расчет по образованию трещин) принимают коэффициент надежности по нагрузке
(как при расчете по прочности). При расчете по раскрытию трещин и по деформациям (включая вспомогательный расчет по образованию трещин) принимают коэффициент надежности по нагрузке 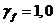 .
.
Расчет железобетонных элементов
по образованию и раскрытию трещин
8. 2. 4. Расчет железобетонных элементов по образованию трещин производят из условия:
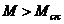 ; (8. 116)
; (8. 116)
где M - изгибающий момент от внешней нагрузки относительно оси, нормальной к плоскости действия момента и проходящей через центр тяжести приведенного поперечного сечения элемента;
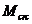 - изгибающий момент, воспринимаемый нормальным сечением элемента при образовании трещин, определяемый по формуле (8. 121).
- изгибающий момент, воспринимаемый нормальным сечением элемента при образовании трещин, определяемый по формуле (8. 121).
Для центрально растянутых элементов образование трещин определяют из условия:
 , (8. 117)
, (8. 117)
где N - продольное растягивающее усилие от внешней нагрузки;
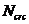 - продольное растягивающее усилие, воспринимаемое элементом при образовании трещин, определяемое согласно 8. 2. 13.
- продольное растягивающее усилие, воспринимаемое элементом при образовании трещин, определяемое согласно 8. 2. 13.
8. 2. 5. В тех случаях, когда выполняются условия (8. 116) или (8. 117), выполняют расчет по раскрытию трещин. Расчет железобетонных элементов производят по непродолжительному и продолжительному раскрытию трещин.
Непродолжительное раскрытие трещин определяют от совместного действия постоянных и временных (длительных и кратковременных) нагрузок, продолжительное - только от постоянных и временных длительных нагрузок (4. 6).
8. 2. 6. Расчет по раскрытию трещин производят из условия:
 , (8. 118)
, (8. 118)
где 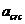 - ширина раскрытия трещин от действия внешней нагрузки, определяемая согласно 8. 2. 7, 8. 2. 15 - 8. 2. 17;
- ширина раскрытия трещин от действия внешней нагрузки, определяемая согласно 8. 2. 7, 8. 2. 15 - 8. 2. 17;
 - предельно допустимая ширина раскрытия трещин.
- предельно допустимая ширина раскрытия трещин.
Значения  принимают равными:
принимают равными:
а) из условия обеспечения сохранности арматуры
классов А240 - А600, В500:
0, 3 мм - при продолжительном раскрытии трещин;
0, 4 мм - при непродолжительном раскрытии трещин;
классов А800, А1000, 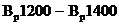 , К1400, К1500 (К-19) и К1500 (К-7), К1600 диаметром 12 мм:
, К1400, К1500 (К-19) и К1500 (К-7), К1600 диаметром 12 мм:
0, 2 мм - при продолжительном раскрытии трещин;
0, 3 мм - при непродолжительном раскрытии трещин;
классов 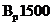 , К1500 (К-7), К1600 диаметром 6 и 9 мм:
, К1500 (К-7), К1600 диаметром 6 и 9 мм:
0, 1 мм - при продолжительном раскрытии трещин;
0, 2 мм - при непродолжительном раскрытии трещин;
б) из условия ограничения проницаемости конструкций
0, 2 мм - при продолжительном раскрытии трещин;
0, 3 мм - при непродолжительном раскрытии трещин.
8. 2. 7. Расчет железобетонных элементов следует производить по продолжительному и по непродолжительному раскрытию нормальных и наклонных трещин.
Ширину продолжительного раскрытия трещин определяют по формуле
 , (8. 119)
, (8. 119)
а ширину непродолжительного раскрытия трещин - по формуле
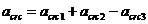 , (8. 120)
, (8. 120)
где 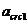 - ширина раскрытия трещин от продолжительного действия постоянных и временных длительных нагрузок;
- ширина раскрытия трещин от продолжительного действия постоянных и временных длительных нагрузок;
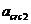 - ширина раскрытия трещин от непродолжительного действия постоянных и временных (длительных и кратковременных) нагрузок;
- ширина раскрытия трещин от непродолжительного действия постоянных и временных (длительных и кратковременных) нагрузок;
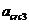 - ширина раскрытия трещин от непродолжительного действия постоянных и временных длительных нагрузок.
- ширина раскрытия трещин от непродолжительного действия постоянных и временных длительных нагрузок.
Определение момента образования трещин,
нормальных к продольной оси элемента
8. 2. 8. Изгибающий момент 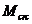 при образовании трещин в общем случае определяется по деформационной модели согласно 8. 2. 14.
при образовании трещин в общем случае определяется по деформационной модели согласно 8. 2. 14.
Для элементов прямоугольного, таврового или двутаврового сечения с арматурой, расположенной у верхней и нижней граней, момент трещинообразования с учетом неупругих деформаций растянутого бетона допускается определять согласно указаниям 8. 2. 10 - 8. 2. 12.
8. 2. 9. Допускается момент образования трещин определять без учета неупругих деформаций растянутого бетона по указаниям 8. 2. 11, принимая в формуле (8. 121) 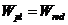 . Если при этом условие (8. 118) или условие (8. 139) не удовлетворяются, то момент образования трещин следует определять с учетом неупругих деформаций растянутого бетона.
. Если при этом условие (8. 118) или условие (8. 139) не удовлетворяются, то момент образования трещин следует определять с учетом неупругих деформаций растянутого бетона.
8. 2. 10. Момент образования трещин с учетом неупругих деформаций растянутого бетона определяют в соответствии со следующими положениями:
сечения после деформирования остаются плоскими;
эпюру напряжений в сжатой зоне бетона принимают треугольной формы, как для упругого тела (рисунок 8. 17);
эпюру напряжений в растянутой зоне бетона принимают трапециевидной формы с напряжениями, не превышающими расчетных значений сопротивления бетона растяжению  ;
;
относительную деформацию крайнего растянутого волокна бетона принимают равной ее предельному значению 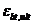 при кратковременном действии нагрузки (8. 1. 30); при двухзначной эпюре деформаций в сечении элемента
при кратковременном действии нагрузки (8. 1. 30); при двухзначной эпюре деформаций в сечении элемента  ;
;
напряжения в арматуре принимают в зависимости от относительных деформаций как для упругого тела.
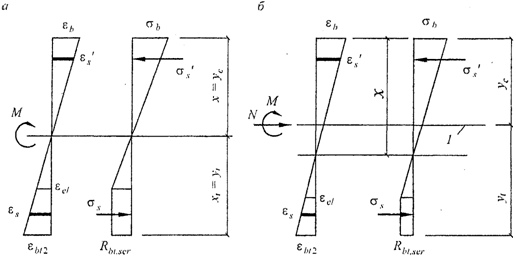
Рисунок 8. 17. Схема напряженно-деформированного состояния
сечения элемента при проверке образования трещин
при действии изгибающего момента (а),
изгибающего момента и продольной силы (б)
8. 2. 11. Момент образования трещин с учетом неупругих деформаций растянутого бетона определяют по формуле
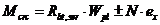 , (8. 121)
, (8. 121)
где 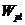 - упругопластический момент сопротивления сечения для крайнего растянутого волокна бетона, определяемый с учетом положений 8. 2. 10;
- упругопластический момент сопротивления сечения для крайнего растянутого волокна бетона, определяемый с учетом положений 8. 2. 10;
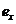 - расстояние от точки приложения продольной силы N (расположенной в центре тяжести приведенного сечения элемента) до ядровой точки, наиболее удаленной от растянутой зоны, трещинообразование которой проверяется.
- расстояние от точки приложения продольной силы N (расположенной в центре тяжести приведенного сечения элемента) до ядровой точки, наиболее удаленной от растянутой зоны, трещинообразование которой проверяется.
В формуле (8. 121) знак " плюс" принимают при сжимающей продольной силе N, " минус" - при растягивающей силе.
Для прямоугольных сечений и тавровых сечений с полкой, расположенной в сжатой зоне, значение 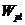 при действии момента в плоскости оси симметрии допускается принимать равным
при действии момента в плоскости оси симметрии допускается принимать равным
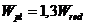 , (8. 122)
, (8. 122)
где 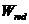 - упругий момент сопротивления приведенного сечения по растянутой зоне сечения, определяемый в соответствии с 8. 2. 12.
- упругий момент сопротивления приведенного сечения по растянутой зоне сечения, определяемый в соответствии с 8. 2. 12.
8. 2. 12. Момент сопротивления 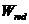 и расстояние
и расстояние 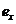 определяют по формулам:
определяют по формулам:
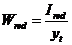 ; (8. 123)
; (8. 123)
 , (8. 124)
, (8. 124)
где 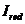 - момент инерции приведенного сечения элемента относительно его центра тяжести
- момент инерции приведенного сечения элемента относительно его центра тяжести
 ; (8. 125)
; (8. 125)
I, 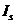 ,
,  - моменты инерции сечений бетона, растянутой арматуры и сжатой арматуры соответственно;
- моменты инерции сечений бетона, растянутой арматуры и сжатой арматуры соответственно;
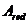 - площадь приведенного поперечного сечения элемента, определяемая по формуле
- площадь приведенного поперечного сечения элемента, определяемая по формуле
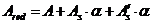 ; (8. 126)
; (8. 126)
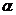 - коэффициент приведения арматуры к бетону
- коэффициент приведения арматуры к бетону
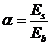 ;
;
A, 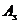 ,
, 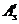 - площади поперечного сечения бетона, растянутой и сжатой арматуры соответственно;
- площади поперечного сечения бетона, растянутой и сжатой арматуры соответственно;
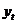 - расстояние от наиболее растянутого волокна бетона до центра тяжести приведенного поперечного сечения элемента
- расстояние от наиболее растянутого волокна бетона до центра тяжести приведенного поперечного сечения элемента
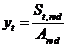 ,
,
здесь 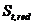 - статический момент площади приведенного поперечного сечения элемента относительно наиболее растянутого волокна бетона.
- статический момент площади приведенного поперечного сечения элемента относительно наиболее растянутого волокна бетона.
Допускается момент сопротивления 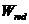 определять без учета арматуры.
определять без учета арматуры.
8. 2. 13. Усилие 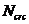 при образовании трещин в центрально растянутых элементах определяют по формуле
при образовании трещин в центрально растянутых элементах определяют по формуле
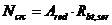 . (8. 127)
. (8. 127)
8. 2. 14. Определение момента образования трещин на основе нелинейной деформационной модели производят исходя из общих положений, приведенных в 6. 1. 24 и 8. 1. 20 - 8. 1. 30, но с учетом работы бетона в растянутой зоне нормального сечения, определяемой диаграммой состояния растянутого бетона согласно 6. 1. 22. Расчетные характеристики материалов принимают для предельных состояний второй группы.
Значение 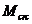 определяют из решения системы уравнений, представленных в 8. 1. 20 - 8. 1. 30, принимая относительную деформацию бетона
определяют из решения системы уравнений, представленных в 8. 1. 20 - 8. 1. 30, принимая относительную деформацию бетона 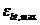 у растянутой грани элемента от действия внешней нагрузки, равной предельному значению относительной деформации бетона при растяжении
у растянутой грани элемента от действия внешней нагрузки, равной предельному значению относительной деформации бетона при растяжении 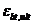 , определяемому согласно указаниям 8. 1. 30.
, определяемому согласно указаниям 8. 1. 30.
Расчет ширины раскрытия трещин,
нормальных к продольной оси элемента
8. 2. 15. Ширину раскрытия нормальных трещин 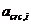 (i = 1, 2, 3 - см. 8. 2. 7) определяют по формуле
(i = 1, 2, 3 - см. 8. 2. 7) определяют по формуле
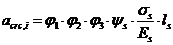 , (8. 128)
, (8. 128)
где 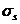 - напряжение в продольной растянутой арматуре в нормальном сечении с трещиной от соответствующей внешней нагрузки, определяемое согласно 8. 2. 16;
- напряжение в продольной растянутой арматуре в нормальном сечении с трещиной от соответствующей внешней нагрузки, определяемое согласно 8. 2. 16;
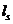 - базовое (без учета влияния вида поверхности арматуры) расстояние между смежными нормальными трещинами, определяемое согласно 8. 2. 17;
- базовое (без учета влияния вида поверхности арматуры) расстояние между смежными нормальными трещинами, определяемое согласно 8. 2. 17;
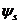 - коэффициент, учитывающий неравномерное распределение относительных деформаций растянутой арматуры между трещинами; допускается принимать коэффициент
- коэффициент, учитывающий неравномерное распределение относительных деформаций растянутой арматуры между трещинами; допускается принимать коэффициент  ; если при этом условие (8. 118) не удовлетворяется, то значение
; если при этом условие (8. 118) не удовлетворяется, то значение 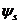 следует определять по формуле (8. 138);
следует определять по формуле (8. 138);
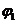 - коэффициент, учитывающий продолжительность действия нагрузки, принимаемый равным:
- коэффициент, учитывающий продолжительность действия нагрузки, принимаемый равным:
1, 0 - при непродолжительном действии нагрузки;
1, 4 - при продолжительном действии нагрузки;
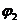 - коэффициент, учитывающий профиль продольной арматуры, принимаемый равным:
- коэффициент, учитывающий профиль продольной арматуры, принимаемый равным:
0, 5 - для арматуры периодического профиля и канатной;
0, 8 - для гладкой арматуры;
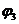 - коэффициент, учитывающий характер нагружения, принимаемый равным:
- коэффициент, учитывающий характер нагружения, принимаемый равным:
1, 0 - для элементов изгибаемых и внецентренно сжатых;
1, 2 - для растянутых элементов.
8. 2. 16. Значения напряжения 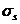 в растянутой арматуре изгибаемых элементов определяют по формуле
в растянутой арматуре изгибаемых элементов определяют по формуле
 , (8. 129)
, (8. 129)
где 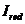 ,
, 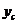 - момент инерции и высота сжатой зоны приведенного поперечного сечения элемента, определяемые с учетом площади сечения только сжатой зоны бетона, площадей сечения растянутой и сжатой арматуры согласно 8. 2. 27, принимая в соответствующих формулах значения коэффициента приведения арматуры к бетону
- момент инерции и высота сжатой зоны приведенного поперечного сечения элемента, определяемые с учетом площади сечения только сжатой зоны бетона, площадей сечения растянутой и сжатой арматуры согласно 8. 2. 27, принимая в соответствующих формулах значения коэффициента приведения арматуры к бетону 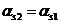 .
.
Для изгибаемых элементов 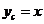 (рисунок 8. 18), где x - высота сжатой зоны бетона, определяемая согласно 8. 2. 28 при
(рисунок 8. 18), где x - высота сжатой зоны бетона, определяемая согласно 8. 2. 28 при 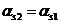 .
.

I - уровень центра тяжести приведенного поперечного сечения
Рисунок 8. 18. Схема напряженно-деформированного состояния
элемента с трещинами при действии изгибающего момента
(а, б), изгибающего момента и продольной силы (в)
Значение коэффициента приведения арматуры к бетону  определяют по формуле
определяют по формуле
 , (8. 130)
, (8. 130)
где 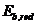 - приведенный модуль деформации сжатого бетона, учитывающий неупругие деформации сжатого бетона и определяемый по формуле
- приведенный модуль деформации сжатого бетона, учитывающий неупругие деформации сжатого бетона и определяемый по формуле
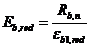 . (8. 131)
. (8. 131)
Относительную деформацию бетона 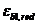 принимают равной 0, 0015.
принимают равной 0, 0015.
Допускается напряжение 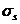 определять по формуле
определять по формуле
 , (8. 132)
, (8. 132)
где 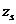 - расстояние от центра тяжести растянутой арматуры до точки приложения равнодействующей усилий в сжатой зоне элемента.
- расстояние от центра тяжести растянутой арматуры до точки приложения равнодействующей усилий в сжатой зоне элемента.
Для элементов прямоугольного поперечного сечения при отсутствии (или без учета) сжатой арматуры значение 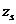 определяют по формуле
определяют по формуле
 . (8. 133)
. (8. 133)
Для элементов прямоугольного, таврового (с полкой в сжатой зоне) и двутаврового поперечного сечения допускается значение 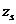 принимать равным
принимать равным 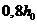 .
.
При действии изгибающего момента M и продольной силы N напряжение 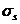 в растянутой арматуре определяют по формуле
в растянутой арматуре определяют по формуле
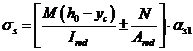 , (8. 134)
, (8. 134)
где 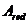 ,
, 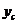 - площадь приведенного поперечного сечения элемента и расстояние от наиболее сжатого волокна бетона до центра тяжести приведенного сечения, определяемые по общим правилам расчета геометрических характеристик сечений упругих элементов с учетом площади сечения только сжатой зоны бетона, площадей сечения растянутой и сжатой арматуры согласно 8. 2. 28, принимая коэффициент приведения арматуры к бетону
- площадь приведенного поперечного сечения элемента и расстояние от наиболее сжатого волокна бетона до центра тяжести приведенного сечения, определяемые по общим правилам расчета геометрических характеристик сечений упругих элементов с учетом площади сечения только сжатой зоны бетона, площадей сечения растянутой и сжатой арматуры согласно 8. 2. 28, принимая коэффициент приведения арматуры к бетону  .
.
Допускается напряжение 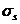 определять по формуле
определять по формуле
 , (8. 135)
, (8. 135)
где 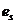 - расстояние от центра тяжести растянутой арматуры до точки приложения продольной силы N с учетом эксцентриситета, равного
- расстояние от центра тяжести растянутой арматуры до точки приложения продольной силы N с учетом эксцентриситета, равного 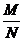 .
.
Для элементов прямоугольного сечения при отсутствии (или без учета) сжатой арматуры значение 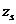 допускается определять по формуле (8. 133), в которой
допускается определять по формуле (8. 133), в которой 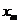 - высота сжатой зоны бетона с учетом влияния продольной силы, определяемая согласно 8. 2. 28, принимая коэффициент приведения арматуры к бетону
- высота сжатой зоны бетона с учетом влияния продольной силы, определяемая согласно 8. 2. 28, принимая коэффициент приведения арматуры к бетону 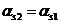 .
.
Для элементов прямоугольного, таврового (с полкой в сжатой зоне) и двутаврового поперечного сечения допускается значение 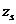 принимать равным
принимать равным 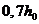 .
.
В формулах (8. 134) и (8. 135) знак " плюс" принимают при растягивающей, а знак " минус" при сжимающей продольной силе.
Напряжения 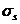 не должны превышать
не должны превышать 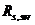 .
.
8. 2. 17. Значения базового расстояния между трещинами 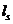 определяют по формуле
определяют по формуле
 (8. 136)
(8. 136)
и принимают не менее 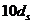 и 10 см и не более
и 10 см и не более 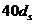 и 40 см.
и 40 см.
Здесь 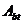 - площадь сечения растянутого бетона;
- площадь сечения растянутого бетона;
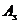 - площадь сечения растянутой арматуры;
- площадь сечения растянутой арматуры;
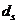 - номинальный диаметр арматуры.
- номинальный диаметр арматуры.
Значения 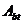 определяют по высоте растянутой зоны бетона
определяют по высоте растянутой зоны бетона 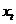 , используя правила расчета момента образования трещин согласно указаниям 8. 2. 8 - 8. 2. 14.
, используя правила расчета момента образования трещин согласно указаниям 8. 2. 8 - 8. 2. 14.
В любом случае значение 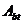 принимают равным площади сечения при ее высоте в пределах не менее 2a и не более 0, 5h.
принимают равным площади сечения при ее высоте в пределах не менее 2a и не более 0, 5h.
8. 2. 18. Значения коэффициента 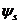 определяют по формуле
определяют по формуле
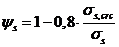 , (8. 137)
, (8. 137)
где 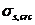 - напряжение в продольной растянутой арматуре в сечении с трещиной сразу после образования нормальных трещин, определяемое по указаниям 8. 2. 16, принимая в соответствующих формулах значения
- напряжение в продольной растянутой арматуре в сечении с трещиной сразу после образования нормальных трещин, определяемое по указаниям 8. 2. 16, принимая в соответствующих формулах значения  ;
;
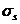 - то же, при действии рассматриваемой нагрузки.
- то же, при действии рассматриваемой нагрузки.
Для изгибаемых элементов значение коэффициента 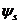 допускается определять по формуле
допускается определять по формуле
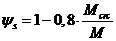 , (8. 138)
, (8. 138)
где 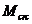 определяют по формуле (8. 121).
определяют по формуле (8. 121).
Расчет элементов железобетонных конструкций по деформациям
8. 2. 19. Расчет элементов железобетонных конструкций по деформациям производят с учетом эксплуатационных требований, предъявляемых к конструкциям.
Расчет по деформациям следует производить на действие:
постоянных, временных длительных и кратковременных нагрузок (см. 4. 6) при ограничении деформаций технологическими или конструктивными требованиями;
постоянных и временных длительных нагрузок при ограничении деформаций эстетическими требованиями.
8. 2. 20. Значения предельно допустимых деформаций элементов принимают согласно СП 20. 13330 и нормативным документам на отдельные виды конструкций.
Расчет железобетонных элементов по прогибам
8. 2. 21. Расчет железобетонных элементов по прогибам производят из условия:
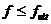 , (8. 139)
, (8. 139)
где f - прогиб железобетонного элемента от действия внешней нагрузки;
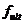 - значение предельно допустимого прогиба железобетонного элемента.
- значение предельно допустимого прогиба железобетонного элемента.
Прогибы железобетонных конструкций определяют по общим правилам строительной механики в зависимости от изгибных, сдвиговых и осевых деформационных характеристик железобетонного элемента в сечениях по его длине (кривизн, углов сдвига и т. д. ).
В тех случаях, когда прогибы железобетонных элементов в основном зависят от изгибных деформаций, значения прогибов определяют по жесткостным характеристикам согласно 8. 2. 22 и 8. 2. 31.
8. 2. 22. Для изгибаемых элементов постоянного по длине элемента сечения, не имеющих трещин, прогибы определяют по общим правилам строительной механики с использованием жесткости поперечных сечений, определяемой по формуле (8. 143).
Определение кривизны железобетонных элементов
8. 2. 23. Кривизну изгибаемых, внецентренно сжатых и внецентренно растянутых элементов для вычисления их прогибов определяют:
а) для элементов или участков элемента, где в растянутой зоне не образуются нормальные к продольной оси трещины, согласно 8. 2. 24, 8. 2. 26;
б) для элементов или участков элемента, где в растянутой зоне имеются трещины, согласно 8. 2. 24, 8. 2. 25 и 8. 2. 27.
Элементы или участки элементов рассматривают без трещин, если трещины не образуются [т. е. условие (8. 116) не выполняется] при действии полной нагрузки, включающей постоянную, временную длительную и кратковременную нагрузки.
Кривизну железобетонных элементов с трещинами и без трещин можно также определять на основе деформационной модели согласно 8. 2. 32.
8. 2. 24. Полную кривизну изгибаемых, внецентренно сжатых и внецентренно растянутых элементов определяют по формулам:
для участков без трещин в растянутой зоне
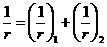 ; (8. 140)
; (8. 140)
для участков с трещинами в растянутой зоне
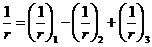 . (8. 141)
. (8. 141)
В формуле (8. 140):
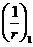 ,
, 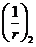 - кривизны соответственно от непродолжительного действия кратковременных нагрузок и от продолжительного действия постоянных и временных длительных нагрузок.
- кривизны соответственно от непродолжительного действия кратковременных нагрузок и от продолжительного действия постоянных и временных длительных нагрузок.
В формуле (8. 141):
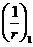 - кривизна от непродолжительного действия всей нагрузки, на которую производят расчет по деформациям;
- кривизна от непродолжительного действия всей нагрузки, на которую производят расчет по деформациям;
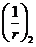 - кривизна от непродолжительного действия постоянных и временных длительных нагрузок;
- кривизна от непродолжительного действия постоянных и временных длительных нагрузок;
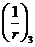 - кривизна от продолжительного действия постоянных и временных длительных нагрузок.
- кривизна от продолжительного действия постоянных и временных длительных нагрузок.
Кривизны 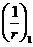 ,
, 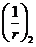 и
и 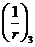 - определяют согласно указаниям 8. 2. 25.
- определяют согласно указаниям 8. 2. 25.
8. 2. 25. Кривизну железобетонных элементов 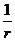 от действия соответствующих нагрузок (8. 2. 24) определяют по формуле
от действия соответствующих нагрузок (8. 2. 24) определяют по формуле
 , (8. 142)
, (8. 142)
где M - изгибающий момент от внешней нагрузки (с учетом момента от продольной силы N) относительно оси, нормальной плоскости действия изгибающего момента и проходящей через центр тяжести приведенного поперечного сечения элемента;
D - изгибная жесткость приведенного поперечного сечения элемента, определяемая по формуле
 , (8. 143)
, (8. 143)
где 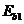 - модуль деформации сжатого бетона, определяемый в зависимости от продолжительности действия нагрузки и с учетом наличия или отсутствия трещин;
- модуль деформации сжатого бетона, определяемый в зависимости от продолжительности действия нагрузки и с учетом наличия или отсутствия трещин;
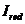 - момент инерции приведенного поперечного сечения относительно его центра тяжести, определяемый с учетом наличия или отсутствия трещин.
- момент инерции приведенного поперечного сечения относительно его центра тяжести, определяемый с учетом наличия или отсутствия трещин.
Значения модуля деформации бетона 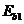 и момента инерции приведенного сечения
и момента инерции приведенного сечения 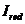 для элементов без трещин в растянутой зоне и с трещинами определяют по указаниям 8. 2. 26 и 8. 2. 27 соответственно.
для элементов без трещин в растянутой зоне и с трещинами определяют по указаниям 8. 2. 26 и 8. 2. 27 соответственно.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|