СВОД ПРАВИЛ 9 страница

⇐ ПредыдущаяСтр 9 из 19Следующая ⇒

а) если продольная сила N приложена между равнодействующими усилий в арматуре S и S' (рисунок 8. 4, а) - из условий

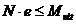; (8. 20)

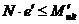, (8. 21)

где 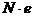и 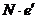- усилия от внешних нагрузок;

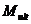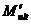и - предельные усилия, которые может воспринять сечение.

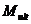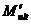Усилия и определяют по формулам

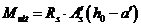; (8. 22)

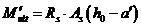; (8. 23)

б) если продольная сила N приложена за пределами расстояния между равнодействующими усилий в арматуре S и S' (рисунок 8. 4, б) - из условия (8. 20), определяя предельный момент 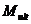по формуле

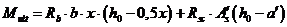, (8. 24)

при этом высоту сжатой зоны x определяют по формуле

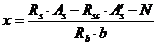. (8. 25)

а)

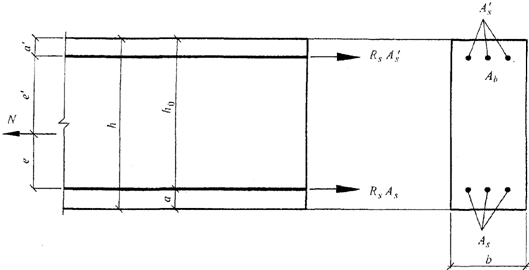
б)

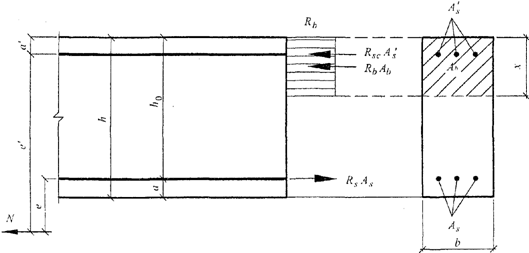
а - между равнодействующими усилий в арматуре S и S';

б - за пределами расстояний между равнодействующими

усилий в арматуре S и S'

Рисунок 8. 4. Схема усилий и эпюра напряжений в сечении,

нормальном к продольной оси внецентренно растянутого

железобетонного элемента, при расчете его по прочности

при приложении продольной силы N

Если полученное из расчета по формуле (8. 25) значение 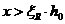, в формулу (8. 24) подставляют 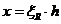, где 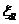определяют согласно указаниям 8. 1. 6.

Расчет по прочности нормальных сечений

на основе нелинейной деформационной модели

8. 1. 20. При расчете по прочности усилия и деформации в сечении, нормальном к продольной оси элемента, определяют на основе нелинейной деформационной модели, использующей уравнения равновесия внешних сил и внутренних усилий в сечении элемента, а также следующих положений:

распределение относительных деформаций бетона и арматуры по высоте сечения элемента принимают по линейному закону (гипотеза плоских сечений);

связь между осевыми напряжениями и относительными деформациями бетона и арматуры принимают в виде диаграмм состояния (деформирования) бетона и арматуры;

сопротивление бетона растянутой зоны допускается не учитывать, принимая при 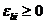напряжения 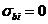. В отдельных случаях (например, изгибаемые и внецентренно сжатые бетонные конструкции, в которых не допускают трещины) расчет по прочности производят с учетом работы растянутого бетона.

8. 1. 21. Переход от эпюры напряжений в бетоне к обобщенным внутренним усилиям определяют с помощью процедуры численного интегрирования напряжений по нормальному сечению. Для этого нормальное сечение условно разделяют на малые участки: при косом внецентренном сжатии (растяжении) и косом изгибе - по высоте и ширине сечения; при внецентренном сжатии (растяжении) и изгибе в плоскости оси симметрии поперечного сечения элемента - только по высоте сечения. Напряжения в пределах малых участков принимают равномерно распределенными (усредненными).

8. 1. 22. При расчете элементов с использованием деформационной модели принимают:

значения сжимающей продольной силы, а также сжимающих напряжений и деформаций укорочения бетона и арматуры со знаком " минус";

значения растягивающей продольной силы, а также растягивающих напряжений и деформаций удлинения бетона и арматуры со знаком " плюс".

Знаки координат центров тяжести арматурных стержней и выделенных участков бетона, а также точки приложения продольной силы принимают в соответствии с назначенной системой координат XOY. В общем случае начало координат этой системы (точка 0 на рисунке 8. 5) располагают в произвольном месте в пределах поперечного сечения элемента.

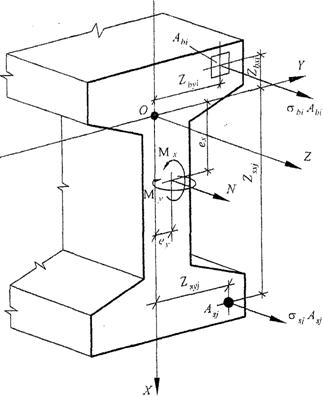
Рисунок 8. 5. Расчетная схема нормального сечения

железобетонного элемента

8. 1. 23. При расчете нормальных сечений по прочности в общем случае (см. рисунок 8. 5) используют:

уравнения равновесия внешних сил и внутренних усилий в нормальном сечении элемента:

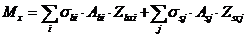; (8. 26)

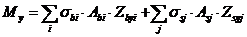; (8. 27)

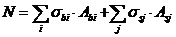; (8. 28)

уравнения, определяющие распределение деформаций по сечению элемента

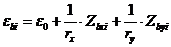; (8. 29)

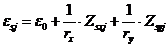; (8. 30)

зависимости, связывающие напряжения и относительные деформации бетона и арматуры

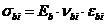; (8. 31)

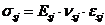. (8. 32)

В уравнениях (8. 26) - (8. 32):

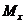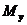, - изгибающие моменты от внешней нагрузки относительно выбранных и располагаемых в пределах поперечного сечения элемента координатных осей (соответственно действующих в плоскостях XOZ и YOZ или параллельно им), определяемые по формулам:

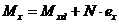; (8. 33)

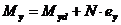; (8. 34)

здесь 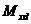, 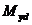- изгибающие моменты в соответствующих плоскостях от внешней нагрузки, определяемые из статического расчета конструкции;

N - продольная сила от внешней нагрузки;

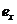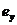, - расстояния от точки приложения продольной силы N до соответствующих выбранных осей;

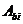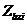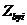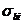, , , - площадь, координаты центра тяжести i-го участка бетона и напряжение на уровне его центра тяжести;

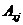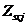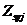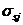, , , - площадь, координаты центра тяжести j-го стержня арматуры и напряжение в нем;

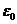- относительная деформация волокна, расположенного на пересечении выбранных осей (в точке 0);

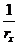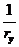, - кривизна продольной оси в рассматриваемом поперечном сечении элемента в плоскостях действия изгибающих моментов 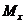и ;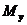

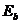- начальный модуль упругости бетона;

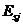- модуль упругости j-го стержня арматуры;

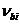- коэффициент упругости бетона i-го участка;

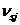- коэффициент упругости j-го стержня арматуры.

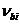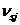Коэффициенты и принимают по соответствующим диаграммам состояния бетона и арматуры, указанным в 6. 1. 19, 6. 2. 13.

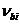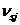Значения коэффициентов и определяют как соотношение значений напряжений и деформаций для рассматриваемых точек соответствующих диаграмм состояния бетона и арматуры, принятых в расчете, деленное на модуль упругости бетона 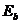и арматуры 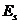(при двухлинейной диаграмме состояния бетона - на приведенный модуль деформации сжатого бетона 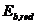). При этом используют зависимости " напряжение-деформация" (6. 5) - (6. 9), (6. 14) и (6. 15) на рассматриваемых участках диаграмм.

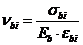; (8. 35)

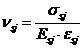. (8. 36)

8. 1. 24. Расчет нормальных сечений железобетонных элементов по прочности производят из условий:

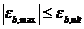; (8. 37)

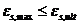, (8. 38)

где 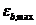- относительная деформация наиболее сжатого волокна бетона в нормальном сечении элемента от действия внешней нагрузки;

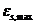- относительная деформация наиболее растянутого стержня арматуры в нормальном сечении элемента от действия внешней нагрузки;

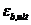- предельное значение относительной деформации бетона при сжатии, принимаемое согласно указаниям 8. 1. 30;

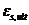- предельное значение относительной деформации удлинения арматуры, принимаемое согласно указаниям 8. 1. 30.

8. 1. 25. Для железобетонных элементов, на которые действуют изгибающие моменты двух направлений и продольная сила (рисунок 8. 5), деформации бетона 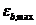и арматуры 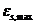в нормальном сечении произвольной формы определяют из решения системы уравнений (8. 39) - (8. 41) с использованием уравнений (8. 29) и (8. 30)

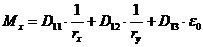; (8. 39)

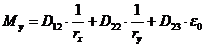; (8. 40)

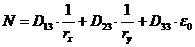. (8. 41)

Жесткостные характеристики (i, j - 1, 2, 3) в системе уравнений (8. 39) - (8. 41) определяют по формулам

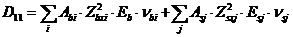; (8. 42)

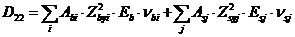; (8. 43)

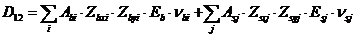; (8. 44)

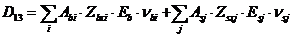; (8. 45)

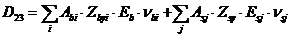; (8. 46)

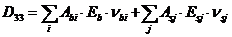. (8. 47)

Обозначения в формулах - см. 8. 1. 23.

8. 1. 26. Для железобетонных элементов, на которые действуют только изгибающие моменты двух направлени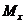й и 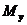(косой изгиб), в уравнении (8. 41) принимают N = 0.

8. 1. 27. Для внецентренно сжатых в плоскости симметрии поперечного сечения железобетонных элементов и расположении оси X в этой плоскости принимают 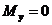и 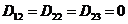. В этом случае уравнения равновесия имеют вид:

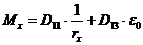; (8. 48)

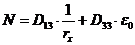. (8. 49)

8. 1. 28. Для изгибаемых в плоскости симметрии поперечного сечения железобетонных элементов и расположения оси X в этой плоскости принимают N = 0, 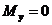, 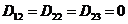. В этом случае уравнения равновесия имеют вид:

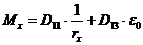; (8. 50)

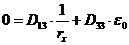. (8. 51)

8. 1. 29. Расчет по прочности нормальных сечений внецентренно сжатых бетонных элементов при расположении продольной сжимающей силы в пределах поперечного сечения элемента производят из условия (8. 37) согласно указаниям 8. 1. 24 - 8. 1. 28, принимая в формулах 8. 1. 25 для определения площадь арматуры .

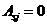Для изгибаемых и внецентренно сжатых бетонных элементов, в которых не допускаются трещины, расчет производят с учетом работы растянутого бетона в поперечном сечении элемента из условия

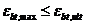, (8. 52)

где 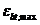- относительная деформация наиболее растянутого волокна бетона в нормальном сечении элемента от действия внешней нагрузки, определяемая согласно 8. 1. 25 - 8. 1. 28;

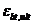- предельное значение относительной деформации бетона при растяжении, принимаемое согласно указаниям 8. 1. 30.

8. 1. 30. Предельные значения относительных деформаций бетона принимают при двузначной эпюре деформаций (сжатие и растяжение) в поперечном сечении бетона элемента (изгиб, внецентренное сжатие или растяжение с большими эксцентриситетами) равными .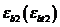

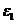При внецентренном сжатии или растяжении элементов и распределении в поперечном сечении бетона элемента деформаций только одного знака предельные значения относительных деформаций бетона определяют в зависимости от соотношения деформаций бетона на противоположных гранях сечения элемента и 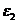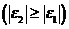по формулам:

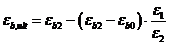, (8. 53)

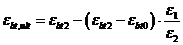, (8. 54)

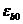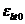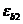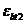где , , и - деформационные параметры расчетных диаграмм состояния бетона (6. 1. 14, 6. 1. 20, 6. 1. 22).

Предельные значения относительной деформации арматуры 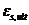принимают равными:

0, 025 - для арматуры с физическим пределом текучести;

0, 015 - для арматуры с условным пределом текучести.

Расчет по прочности железобетонных элементов

при действии поперечных сил

Общие положения

8. 1. 31. Расчет по прочности железобетонных элементов при действии поперечных сил производят на основе модели наклонных сечений.

При расчете по модели наклонных сечений должны быть обеспечены прочность элемента по полосе между наклонными сечениями и наклонному сечению на действие поперечных сил, а также прочность по наклонному сечению на действие момента.

Прочность по наклонной полосе характеризуется максимальным значением поперечной силы, которое может быть воспринято наклонной полосой, находящейся под воздействием сжимающих усилий вдоль полосы и растягивающих усилий от поперечной арматуры, пересекающей наклонную полосу. При этом прочность бетона определяют по сопротивлению бетона осевому сжатию с учетом влияния сложного напряженного состояния в наклонной полосе.

Расчет по наклонному сечению на действие поперечных сил производят на основе уравнения равновесия внешних и внутренних поперечных сил, действующих в наклонном сечении с длиной проекции C на продольную ось элемента. Внутренние поперечные силы включают поперечную силу, воспринимаемую бетоном в наклонном сечении, и поперечную силу, воспринимаемую пересекающей наклонное сечение поперечной арматурой. При этом поперечные силы, воспринимаемые бетоном и поперечной арматурой, определяют по сопротивлениям бетона и поперечной арматуры растяжению с учетом длины проекции C наклонного сечения.

Расчет по наклонному сечению на действие момента производят на основе уравнения равновесия моментов от внешних и внутренних сил, действующих в наклонном сечении с длиной проекции C на продольную ось элемента. Моменты от внутренних сил включают момент, воспринимаемый пересекающей наклонное сечение продольной растянутой арматурой, и момент, воспринимаемый пересекающей наклонное сечение поперечной арматурой. При этом моменты, воспринимаемые продольной и поперечной арматурой, определяют по сопротивлениям продольной и поперечной арматуры растяжению с учетом длины проекции C наклонного сечения.

Расчет железобетонных элементов по полосе между

наклонными сечениями

8. 1. 32. Расчет изгибаемых железобетонных элементов по бетонной полосе между наклонными сечениями производят из условия

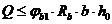, (8. 55)

где Q - поперечная сила в нормальном сечении элемента;

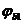- коэффициент, принимаемый равным 0, 3.

Расчет железобетонных элементов по наклонным сечениям

на действие поперечных сил

8. 1. 33. Расчет изгибаемых элементов по наклонному сечению (рисунок 8. 6) производят из условия:

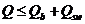, (8. 56)

где Q - поперечная сила в наклонном сечении с длиной проекции C на продольную ось элемента, определяемая от всех внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения; при этом учитывают наиболее опасное загружение в пределах наклонного сечения;

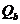- поперечная сила, воспринимаемая бетоном в наклонном сечении;

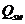- поперечная сила, воспринимаемая поперечной арматурой в наклонном сечении.

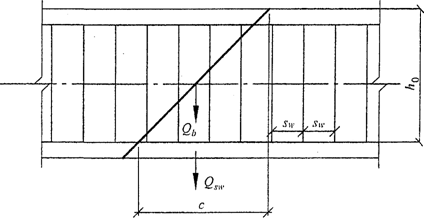
Рисунок 8. 6. Схема усилий при расчете железобетонных

элементов по наклонному сечению на действие

поперечных сил

Поперечную силу 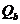определяют по формуле

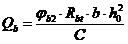, (8. 57)

но принимают не более 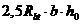и не менее ;

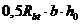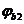- коэффициент, принимаемый равным 1, 5.

Усилие 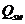для поперечной арматуры, нормальной к продольной оси элемента, определяют по формуле

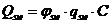, (8. 58)

где 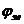- коэффициент, принимаемый равным 0, 75;

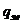- усилие в поперечной арматуре на единицу длины элемента, равное

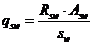. (8. 59)

Расчет производят для ряда расположенных по длине элемента наклонных сечений при наиболее опасной длине проекции наклонного сечения C. При этом длину проекции C в формуле (8. 58) принимают не менее 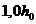и не более .

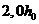Допускается производить расчет наклонных сечений, не рассматривая наклонные сечения при определении поперечной силы от внешней нагрузки, из условия

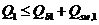, (8. 60)

где 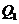- поперечная сила в нормальном сечении от внешней нагрузки;

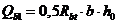; (8. 61)

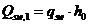. (8. 62)

При расположении нормального сечения, в котором учитывают поперечную силу 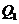, вблизи опоры на расстоянии a менее 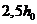расчет из условия (8. 60) производят, умножая значения 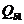, определяемые по формуле (8. 61), на коэффициент, равный 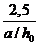, но принимают значение 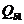не более .

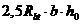При расположении нормального сечения, в котором учитывают поперечную силу 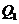, на расстоянии a менее 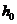расчет из условия (8. 60) производят, умножая значение 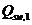, определяемое по формуле (8. 62), на коэффициент, равный .

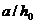Поперечную арматуру учитывают в расчете, если соблюдается условие

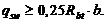
Можно учитывать поперечную арматуру и при невыполнении этого условия, если в условии (8. 56) принимать

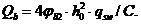
Шаг поперечной арматуры, учитываемой в расчете, 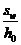должен быть не больше значения .

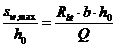При отсутствии поперечной арматуры или нарушении указанных выше требований, а также приведенных в 10. 3 конструктивных требований расчет производят из условий (8. 56) или (8. 60), принимая усилия 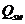или 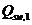равными нулю.

Поперечная арматура должна отвечать конструктивным требованиям, приведенным в 10. 3.

8. 1. 34. Влияние сжимающих и растягивающих напряжений при расчете по полосе между наклонными сечениями и по наклонным сечениям следует учитывать с помощью коэффициента 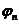, на который умножают правую часть условий (8. 55), (8. 56) или (8. 60).

Значения коэффициента 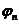принимаются равными:

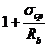при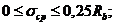

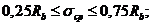
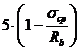1, 25 при

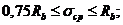
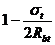при

при ,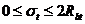

где 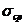- среднее сжимающее напряжение в бетоне от воздействия продольных сил, принимаемое положительным. Величину 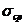принимают как среднее напряжение в сечении элемента с учетом арматуры;

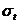- среднее растягивающее напряжение в бетоне от воздействия продольных сил, принимаемое положительным.

Величины 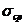и 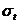принимают как средние напряжения в сечениях элементов. Допускается величины 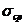и 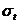определять без учета арматуры при содержании продольной арматуры не более 3%.

Расчет железобетонных элементов по наклонным сечениям

на действие моментов

8. 1. 35. Расчет железобетонных элементов по наклонным сечениям на действие моментов (рисунок 8. 7) производят из условия

⇐ Предыдущая 4 5 6 7 8910 11 12 13 Следующая ⇒