Приклад 2.. Дослідити на умовну та абсолютну збіжність ряд .. Приклад 3.. Знайти область збіжності ряду .. Завдання № 601.

Приклад 2.

Дослідити на умовну та абсолютну збіжність ряд.

Розв’язання:

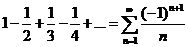- знакозмінний ряд. Розглянемо ряд 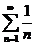, утворений із абсолютних величин ряду 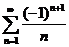. Як відомо, 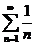- гармонійний ряд, а він є розбіжним.

Застосуємо теорему Лейбніца для дослідження збіжності ряду :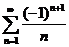

1) 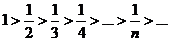- члени ряду утворюють спадну послідовність;

2) .

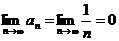Так як ряд 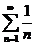- розбіжний, але для ряду 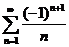виконуються умови теореми Лейбніца, то ряд 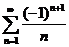збігається умовно■

Приклад 3.

Знайти область збіжності ряду.

Розв’язання:

Застосуємо ознаку Даламбера .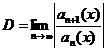

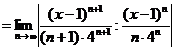
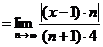
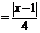Поставимо вимогу, щоб D < 1, тобто .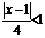

Розв’язуємо цю нерівність. Маємо |x=1| < 4, - 4 < x - 1< 4, -3 < x < 5.

Дослідимо збіжність ряду на кінцях інтервалу, тобто в точках x = - 3 і x = 5.

Підставляючи x = - 3 в даний ряд, маємо: .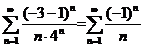

В цьому ряді члени, взяті за абсолютною величиною, спадають і границя n-го члена дорівнює нулю. За ознакою Лейбніця одержаний ряд збігається. Таким чином, точка х = - 3 належить області збіжності ряду.

Підставляючи х = 5 в початковий ряд, маємо: 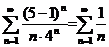- гармонійний ряд, який, як відомо, розбігається. Значить, точка х = 5 не належить області збіжності.

Таким чином, ряд збігається в області х є [-3; 5)■

Завдання № 601.

Дослідити на збіжність ряди

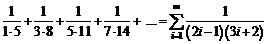
Використаємо для дослідження ряду достатню ознаку порівнянь додатних числових рядів. 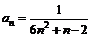- загальний член ряду 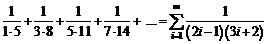. Порівняємо члени даного ряду з членами збіжного загальногармонійного ряду .

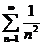Так як члени першого ряду менші за члени загальногармонійного ряду: 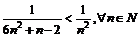, а ряд 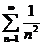– збіжний, то за достатньою ознакою порівнянь додатних числових рядів ряд 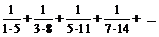також збігається■

⇐ Предыдущая 1 2 345 Следующая ⇒