Приклад 1.

⇐ ПредыдущаяСтр 3 из 5Следующая ⇒

Приклад 1.

Дослідити на збіжність ряди:

1);

2);

3);

4).

Розв’язання:

1) Для дослідження ряду 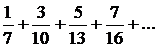скористаємося необхідною умовою збіжності ряду.

Запишемо формулу n-го члена ряду. При виведенні формули скористаємось тим, що чисельник та знаменник дробу утворюють арифметичну прогресію.

n-ий член арифметичної прогресії 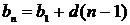, де b₁ – її перший член, d– різниця прогресії.

Тому маємо n-ий член ряду .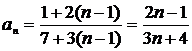

Перевіряємо необхідну ознаку збіжності ряду: 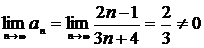. Необхідна ознака збіжності ряду не виконується, тому ряд 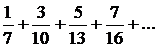розбігається■

2) Застосуємо ознаку Даламбера для дослідження ряду .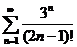

Так як 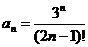, то 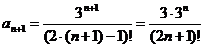. Знаходимо 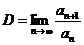= = 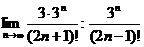= = 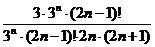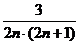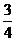< 1.

Так як D < 1, то за ознакою Даламбера даний ряд збігається■

3) Для дослідження збіжності ряду 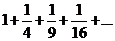застосуємо інтегральну ознаку Коші.

Загальний член числового ряду 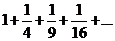задається формулою 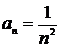. Функція 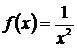є неперервною, додатною і спадною на 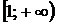, тому можна застосувати інтегральну ознаку Коші.

Обчислимо невласний інтеграл 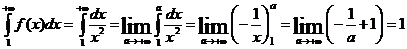. Так як невласний інтеграл 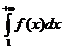збігається, то і числовий ряд 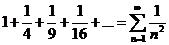також збігається.

Примітка: Можна було провести інші міркування. Ряд 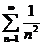- загальногармонійний, він збіжний, так як р = 2■

4) Використаємо для дослідження ряду 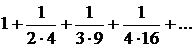достатню ознаку порівнянь додатних числових рядів.

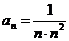- загальний член ряду 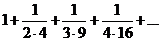(1). Порівняємо члени даного ряду з членами збіжного загальногармонійного ряду 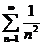(2).

Так як члени ряду (1) менші за члени ряду (2): 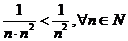, а ряд (2) – збіжний, то за достатньою ознакою порівнянь додатних числових рядів ряд (1) також збігається■

⇐ Предыдущая 1 234 5 Следующая ⇒