
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Достатні ознаки збіжності рядів з додатними членами
Card 1.
1. Theory (payback time)
2. Multiple Integral (easy but interesting)
3. Series (same kind like the previous)
Theoretical questions(Multiple Integrals and Field Theory):
Криволінійні інтеграли другого роду, обчислення, застосування. Незалежність криволінійного інтеграла від шляху інтегрування.
Відновлення функції за повним диференціалом. Фізичне застосування криволінійних інтегралів.
Подвійні інтеграли, їх властивості. Обчислення подвійних інтегралів.
Заміна змінних у подвійних інтегралах, подвійний інтеграл у полярних координатах. Геометричні та механічні застосування.
Потрійні інтеграли. Потрійний інтеграл у циліндричних та сферичних координатах. Поверхневі інтеграли. Формули Остроградського-Гаусса та Стокса.
Curvilinear integrals of the second kind, calculus, applications. Independence of a curvilinear integral of the path of integration.
Restoring function for the complete differential. Physical application of curvilinear integrals.
Double integrals and their properties. Calculating double integrals.
Change of variables in double integrals, the double integral in polar coordinates. Geometrical and mechanical applications.
Triple integrals. Triple integral in cylindrical and spherical coordinates. Surface integrals. Formula Ostrogradskiy - Gauss and Stokes.
Theoretical questions(Series).
1. NumberSeriesandtheirsums. Geometricalprogression. Cuachycriterionandnecessaryconditionofconvergence. Positiveseriesandcomparisontests. D’Alamberttest.
2. Positive Series. The integral test. The root’s test. Series with terms of arbitrary signs. Leibnitz’ test. Operations on series.
3. Functional Series. The domain of convergence. Types of convergence. The simplest properties of functional series. Baisic theorems.
4. Power series. Abel’s Theorem. Properties of power series. Taylor’s Series of elementary functions. Usage of Taylor’s series.
5. Fourier Series. Orthogonal systems. Trigonometric Series. Sufficient condition for the Fourier expansion of a function. Fourier expansion on 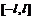 .
.
Practical questions
Завдання: Підрахувати інтеграл( Evaluate the integral)
Завдання: Змінити напрям інтегрування та розрахувати його значення( Change the direction of integration and calculate the value)
Завдання: Дослідити на збіжність ряди(Examine the series)
1. 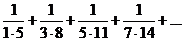 . .
| 11. 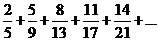 . .
|
2. 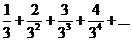 . .
| 12. 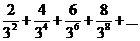 . .
|
3. 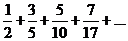 . .
| 13. 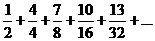 . .
|
4. 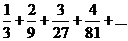 . .
| 14. 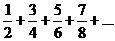 . .
|
5. 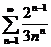 . .
| 15. 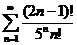 . .
|
6. 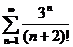 . .
| 16. 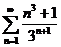 . .
|
7. 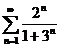 . .
| 17. 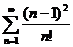 . .
|
8. 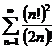 . .
| 18. 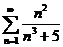 . .
|
9. 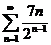 . .
| 19. 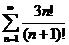 . .
|
10. 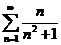 . .
| 20. 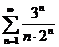 . .
|
Завдання: Дослідити ряд на абсолютну і умовну збіжність (Examine the series)
21. 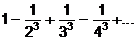 . .
| 31. 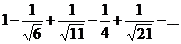 . .
|
22. 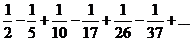 . .
| 32. 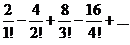 . .
|
23. 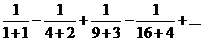 . .
| 33. 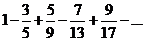 . .
|
24. 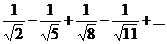 . .
| 34. 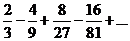 . .
|
25. 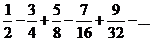 . .
| 35. 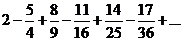 . .
|
26. 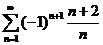 . .
| 36. 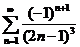 . .
|
27. 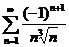 . .
| 37. 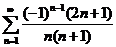 . .
|
28. 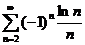 . .
| 38. 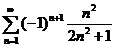 . .
|
29. 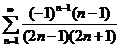 . .
| 39. 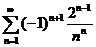 . .
|
30. 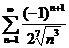 . .
| 40. 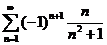 . .
|
Завдання: Знайти область збіжності степеневого ряду (Examine the power series)
41. 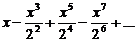 . .
| 61. 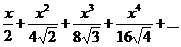 . .
|
42. 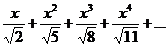 . .
| 62. 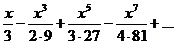 . .
|
43. 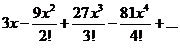 . .
| 63. 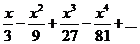 . .
|
44. 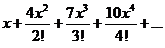 . .
| 64. 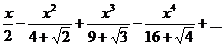 . .
|
45. 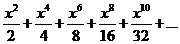 . .
| 65. 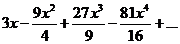
|
46. 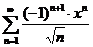 . .
| 66. 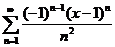 . .
|
47. 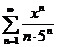 . .
| 67. 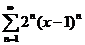 . .
|
48. 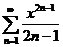 . .
| 68. 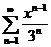 . .
|
49. 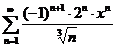 . .
| 69. 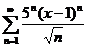 . .
|
50. 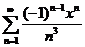 . .
| 70. 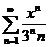 . .
|
51. 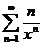 . .
| 71. 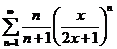 . .
|
52. 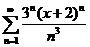 . .
| 72. 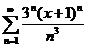 . .
|
53. 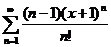 . .
| 73. 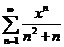 . .
|
54. 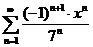 . .
| 74. 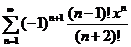 . .
|
55. 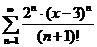 . .
| 75. 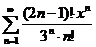 . .
|
56. 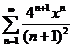 . .
| 76. 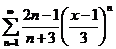 . .
|
57. 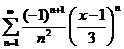 . .
| 77. 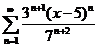 . .
|
58. 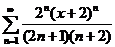 . .
| 78. 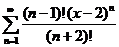 . .
|
59. 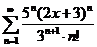 . .
| 79. 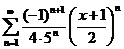 . .
|
60. 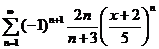 . .
| 80. 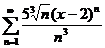 . .
|
РЯДИ
Теоретичні відомості:
Вираз виду 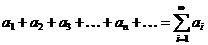 називається рядом, an – загальний член ряду.
називається рядом, an – загальний член ряду.
Сума перших n членів ряду 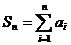 - n-на частинна сума.
- n-на частинна сума.
Ряд називається збіжним, якщо існує  .
.
Ряд називається розбіжним, якщо 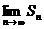 не існує або нескінченість.
не існує або нескінченість.
Гармонійний ряд 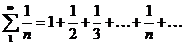 - розбігається.
- розбігається.
Загальногармонійний ряд 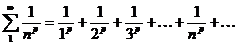 збігається при p> 1 та розбігається при p≤ 1.
збігається при p> 1 та розбігається при p≤ 1.
Геометричний ряд 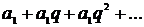 , члени якого утворюють геометричну прогресію зі знаменником q, якщо |q|< 1, то ряд збігається і його сума
, члени якого утворюють геометричну прогресію зі знаменником q, якщо |q|< 1, то ряд збігається і його сума 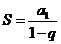 , якщо |q|≥ 1, то ряд розбігається.
, якщо |q|≥ 1, то ряд розбігається.
Необхідна умова збіжності ряду:
Якщо ряд 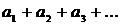 збігається, то
збігається, то 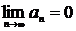 .
.
Якщо 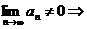 , то ряд розбігається.
, то ряд розбігається.
Достатні ознаки збіжності рядів з додатними членами
1. Ознаки порівнянь для рядів з додатними членами:
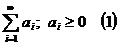
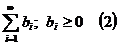
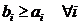
| якщо збігається (2) Þ збігається (1); якщо розбігається (1) Þ розбігається (2). |
2. Ознака Даламбера
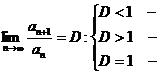
| ряд збігається; ряд розбігається; необхідно провести додатковедослідження. |
3. Ознака Коші
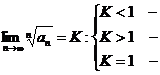
| ряд збігається; ряд розбігається; необхідно провести додаткове дослідження. |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|